A mathematical function (usually written as f(x)) can be thought of as a formula that will return the value of y if you enter a value for x. The inverse of the function f(x) (which is written as f-1(x)) is actually the opposite: enter your y-value and you'll get your initial x-value. Finding the inverse of a function may sound like a complicated process, but for simple equations all you need is knowledge of basic algebraic operations. Read the following step-by-step instructions and illustrated examples.
Step
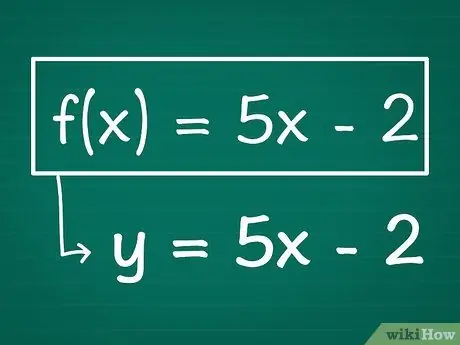
Step 1. Write down your function, replacing f(x) with y if needed
Your formula should have a y alone on one side of the equation, with an x on the other. If you have an equation already written in the form of y and x (for example, 2 + y = 3x2), all you have to do is find the value of y by isolating it on one side of the equation.
- Example: If we have the function f(x) = 5x – 2, we can write it as y = 5x - 2 simply by changing f(x) with y.
- Note: f(x) is the standard function notation, but if you have multiple functions, each function has a different letter to make it easier to tell them apart. For example, g(x) and h(x) are notations to distinguish between the two functions.
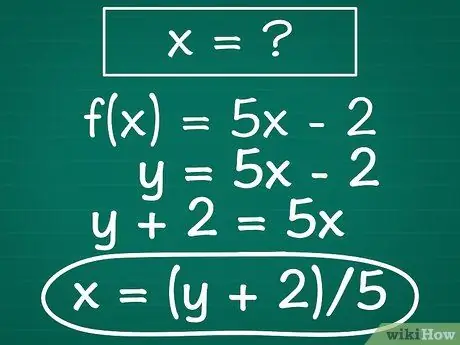
Step 2. Find the value of x
In other words, perform the mathematical operation required to isolate x on one side of the equation. Basic algebraic principles will get you here: if x has a numeric coefficient, divide both sides of the equation by this number; if a number is added to x on one side of the equation, subtract this number from both sides, and so on.
- Remember, you can only perform any operation on one side of the equation as long as you perform the operation on both sides of the equation.
-
Example: Continuing with our example, first, we add 2 to both sides of the equation. The result is y + 2 = 5x. Then we divide both sides of the equation by 5, becoming (y + 2)/5 = x. Finally, to make it easier to read, we'll rewrite the equation with the x on the left side: x = (y + 2)/5.
Step 3. Change the variables
Replace x with y and vice versa. The resulting equation is the inverse of the original equation. In other words, if we plug the value for x into our original equation and get an answer, when we plug that answer into the inverse equation (for the value of x), we get our initial value!
Example: After swapping x and y, we have y = (x + 2)/5
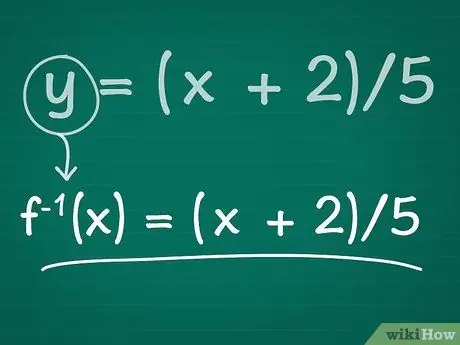
Step 4. Replace y with f-1(x).
The inverse function is usually written in the form f-1(x) = (the part containing x). Note that in this case, the power of -1 doesn't mean we have to perform an exponential operation in our function. This is just a way of showing that this function is the inverse of our original equation.
Since squaring x -1 gives the fraction 1/x, you can also imagine f-1(x) as another way of writing 1/f(x), which also describes the inverse of f(x).
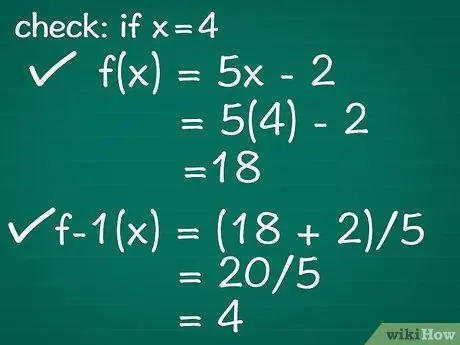
Step 5. Check your work
Try plugging a constant into the original equation for x. If your inverse is correct, then you should be able to plug the answer into the inverse equation and get your initial x value as the answer.
- Example: Let's enter the value x = 4 in our original equation. The result is f(x) = 5(4) – 2 or f(x) = 18.
- Next, let's plug our answer, 18, into our inverse equation for the value of x. If we do this, we get y = (18 + 2)/5, which can be simplified to y = 20/5, which is then simplified to y = 4.4 is our initial value of x, so we know that we have true inverse equation.
Tips
- You can alternate f(x) = y and f^(-1)(x) = y at will when performing algebraic operations in your functions. However, distinguishing between your initial and inverse functions can be confusing, so if you don't complete either function, try using the notation f(x) or f^(-1)(x), which will help you distinguish between the two.
- Note that the inverse of a function is usually, but not always, the function itself.
