How to Find Domain and Range of Functions: 14 Steps (with Pictures)

2024 Author: Jason Gerald | [email protected]. Last modified: 2023-12-16 10:50

Each function has two variables, namely the independent variable and the dependent variable. Literally the value of the dependent variable "depends" on the independent variable. For example, in the function y = f(x) = 2 x + y, x is the independent variable and y is the dependent variable (in other words, y is a function of x). Valid values for the known variable x are called "domains of origin." Valid values for the known y variable are called the “result range.”

Step

Part 1 of 3: Finding the Domain of a Function

Step 1. Decide what type of function you are going to perform

The domain of the function is all x-values (horizontal axis) that will return valid y-values. The equation of the function may be a quadratic, a fraction, or contain a root. To calculate the domain of the function, the first thing you have to do is examine the variables in the equation.

• A quadratic function has the form ax² + bx + c: f(x) = 2x² + 3x + 4
• Examples of functions with fractions include: f(x) = (¹/_x), f(x) = ^(x+1)/_{(x - 1)}, and others.
• Functions that have roots include: f(x) = x, f(x) = (x² + 1), f(x) = -x, and so on.

Step 2. Write down the domain with proper notation

Writing the domain of a function involves using square brackets [,] as well as brackets (,). Use square brackets [,] if the number belongs to the domain and use brackets (,) if the domain does not include the number. The letter U denotes a union that connects parts of the domain that may be separated by a distance.

• For example, the domain of [-2, 10) U (10, 2] includes -2 and 2, but does not include the number 10.
• Always use parentheses () if you are using the infinity symbol,.

Step 3. Draw a graph of the quadratic equation

Quadratic equations produce a parabolic graph that opens up or down. Considering that the parabola will continue infinity on the x-axis, the domain of most quadratic equations is all real numbers. Put another way, a quadratic equation includes all the x-values on the number line, giving the domain R (symbol for all real numbers).

• To solve the function, choose any x-value and enter it into the function. Solving a function with an x-value will return a y-value. The values of x and y are the (x, y) coordinates of a graph of the function.
• Plot these coordinates on a graph and repeat the process with another x-value.
• Plotting some of the values in this model will give you an overview of the shape of the quadratic function.

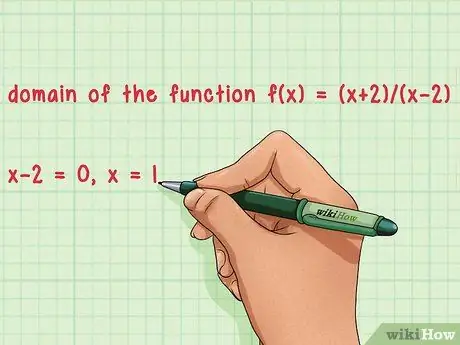
Step 4. If the equation of the function is a fraction, make the denominator equal to zero

When working with fractions, you can never divide by zero. By making the denominator equal to zero and finding the value of x, you can calculate the values to extract from the function.

• For example: Determine the domain of the function f(x) = ^(x+1)/_{(x - 1)}.
• The denominator of the function is (x - 1).
• Make the denominator equal to zero and calculate the value of x: x – 1 = 0, x = 1.
• Write down the domain: The domain of the function does not include 1, but includes all real numbers except 1; therefore, the domain is (-∞, 1) U(1,).
• (-∞, 1) U (1,) can be read as a collection of all real numbers except 1. The symbol for infinity,, represents all real numbers. In this case, all real numbers greater than 1 and less than 1 are included in the domain.

Step 5. If the equation is a root function, make the root variables greater than or equal to zero

You cannot use the square root of a negative number; therefore, any x-value that leads to a negative number must be removed from the function's domain.

• For example: Find the domain of the function f(x) = (x + 3).
• The variables in the root are (x + 3).
• Make the value greater than or equal to zero: (x + 3) 0.
• Calculate the value for x: x -3. Solve for x: x -3.
• The domain of the function includes all real numbers greater than or equal to -3; therefore, the domain is [-3,).

Part 2 of 3: Finding the Range of a Quadratic Equation

Step 1. Make sure you have a quadratic function

The quadratic function has the form ax² + bx + c: f(x) = 2x² + 3x + 4. The graph of the quadratic function is a parabola that opens up or down. There are different ways to calculate the range of the function depending on the type of function you are working on.

The easiest way to determine the range of other functions, such as a root function or a fraction function, is to graph the function using a graphing calculator

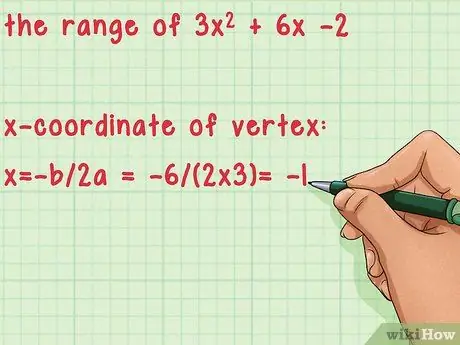
Step 2. Find the x-value of the vertex of the function

The vertex of a quadratic function is the vertex of the parabola. Remember, the form of the quadratic function is ax² + bx + c. To find the x-coordinate use the equation x = -b/2a. The equation is the derivative of a basic quadratic function that represents an equation with zero slope/slope (at the vertex of the graph, the gradient of the function is zero).

• For example, find the range of 3x² + 6x -2.
• Calculate the x-coordinate of the vertex: x = -b/2a = -6/(2*3) = -1

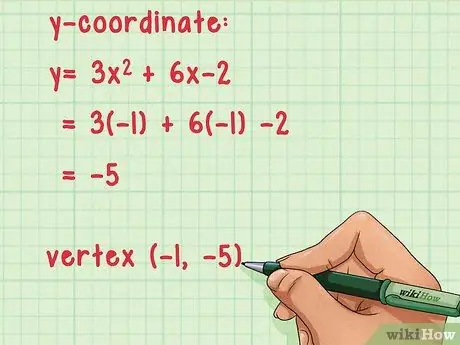
Step 3. Calculate the y-value of the vertex of the function

Plug the x-coordinate into the function to calculate the corresponding y-value of the vertex. This y-value indicates the limit of the range of the function.

• Calculate the y-coordinate: y = 3x² + 6x – 2 = 3(-1)² + 6(-1) -2 = -5.
• The vertex of this function is (-1, -5).

Step 4. Determine the direction of the parabola by plugging in at least one more x-value

Choose any other x-value and plug it into the function to calculate the appropriate y-value. If the y-value is above the vertex, the parabola continues to +∞. If the y-value is below the vertex, the parabola will continue to -∞.

• Use x-value -2: y = 3x² + 6x – 2 = y = 3(-2)² + 6(-2) – 2 = 12 -12 -2 = -2.
• This calculation returns the coordinates (-2, -2).
• These coordinates show you that the parabola continues above the vertex (-1, -5); therefore, the range includes all y-values higher than -5.
• The range of this function is [-5,).

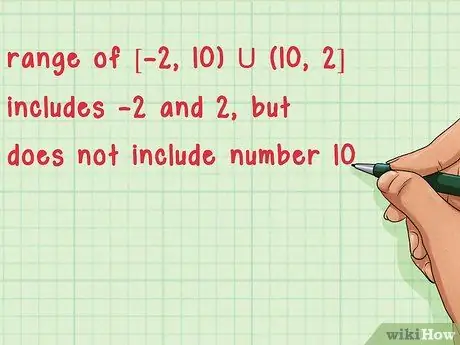
Step 5. Write down the range with proper notation

Like domains, ranges are written with the same notation. Use square brackets [,] if the number is in the range and use brackets (,) if the range does not include the number. The letter U indicates a union that connects parts of the range that may be separated by a distance.

• For example, the range of [-2, 10) U (10, 2] includes -2 and 2, but does not include the number 10.
• Always use parentheses if you are using the infinity symbol,.

Part 3 of 3: Finding the Range from the Graph of a Function

Step 1. Draw the function

Often, the easiest way to determine the range of a function is to graph it. Many root functions have a range (-∞, 0] or [0, +∞) because the vertex of the horizontal parabola (sideways parabola) is on the horizontal x axis. In this case, the function includes all positive y-values if the parabola opens up, or all negative y-values if the parabola opens downwards. Fractional functions will have asymptotes (lines that are never cut by a straight line / curve but are approached to infinity) that define the range of the function.

• Some root functions will start above or below the x-axis. In this case, the range is determined by the number where the root function starts. If the parabola starts at y = -4 and goes up then the range is [-4, +∞).
• The easiest way to draw a function is to use a graphing program or graphing calculator.
• If you don't have a graphing calculator, you can draw a rough sketch of the graph by plugging the x-value into the function and getting the appropriate y-value. Plot these coordinates on a graph to get an idea of what the graph looks like.

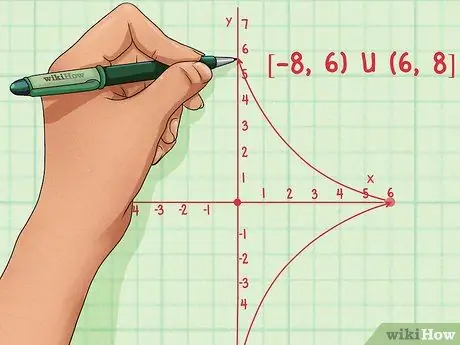
Step 2. Find the minimum value of the function

Immediately after drawing the function, you should be able to clearly see the lowest point of the graph. If there is no clear minimum value, know that some functions will continue at -∞ (infinity).

A fraction function will include all points except those on the asymptotes. The function has a range like (-∞, 6) U (6,)

Step 3. Determine the maximum value of the function

Again, after drawing the graph, you should be able to identify the maximum point of the function. Some functions will continue at +∞ and therefore, will not have a minimum value.

Step 4. Write the range with proper notation

Like domains, ranges are written in the same notation. Use square brackets [,] if the number is in the range and use brackets (,) if the range does not include the number. The letter U indicates a union that connects parts of the range that may be separated by a distance.

• For example, the range of [-2, 10) U (10, 2] includes -2 and 2, but does not include the number 10.
• Always use parentheses if you use the infinity symbol,.