- Author Jason Gerald [email protected].
- Public 2024-01-16 19:04.
- Last modified 2025-06-01 06:05.
Mastering algebra is essential for continuing into almost any type of math, whether in elementary or high school. Every math level has a foundation, so every math level is very important. However, even the most basic algebraic skills can be difficult for beginners to grasp the first time they encounter them. If you're having trouble with basic algebra topics, don't worry - with a little extra explanation, a few easy examples, and a few tips to improve your skills, you'll soon be solving algebra problems like a pro.
Step
Part 1 of 5: Learning the Basic Rules of Algebra

Step 1. Review your basic math operations
To start learning algebra, you'll need to know basic math skills like adding, subtracting, multiplying, and dividing. This primary/elementary school math is very important before you start studying algebra. If you don't master these skills, it will be difficult to complete the more complex concepts taught in algebra. If you need a refresher for these operations, try our article on basic math skills.
You don't have to be good at doing these basic operations in your head to do algebra problems. Many algebra classes allow you to use a calculator to save time when performing these simple operations. However, you should at least know how to perform these operations without a calculator when you are not allowed to use a calculator
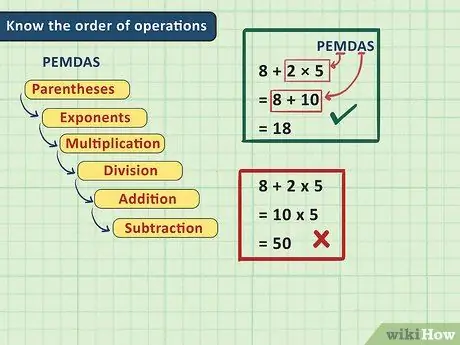
Step 2. Know the order of operations
One of the most tricky things about solving algebraic equations as a beginner is knowing the order in which they start. Fortunately, there is a certain order to solving these problems: first, do any mathematical operation in parentheses, then do the exponents, then multiply, then divide, then add, and finally subtract. A useful means of remembering the order of these operations is the acronym KPKBJK. Learn how to apply the order of operations here. To summarize, the order of operations is:
- Kfail
- Plift/Exponent
- Kali
- Bagain
- Jumlah
- Kshrimp
-
The order of operations is important in algebra because doing the operations in an algebra problem in the wrong order can sometimes affect the answer. For example, if we do the math problem 8 + 2 × 5, if we add 2 and 8 first, we get 10 × 5 = 50, but if we multiply 2 and 5 first, we get 8 + 10 =
Step 18.. Only the second answer is correct.

Step 3. Know how to use negative numbers
In algebra, the use of negative numbers is very common. So it's a good idea to review how to add, subtract, multiply, and divide negative numbers before you start learning algebra. Here are some negative number basics to remember - for more information, check out our articles on adding and subtracting negative numbers and dividing and multiplying negative numbers.
- On a number line, the negative version of a number is the same distance from zero as the positive number is from zero, but in the opposite direction.
- Adding two negative numbers makes the number even more negative (in other words, the digit will be larger, but because the number is negative, the value will be smaller)
- Two negative signs cancel each other out - subtracting a negative number is the same as adding a positive number
- Multiplying or dividing two negative numbers gives a positive answer.
- Multiplying or dividing a positive number and a negative number gives a negative answer.

Step 4. Know how to structure long questions
While simple algebra problems can be easily solved, more complex problems can require many steps. To avoid mistakes, keep your work organized by starting a new line each time you take a step to complete your problem. If you're working with a two-sided equation, try to write all the equals signs (“=”) under the other equals signs. This way, if you make a mistake somewhere, it will be easier to find and correct it.
-
For example, to solve the equation 9/3 - 5 + 3 × 4, we might be able to structure our problem like this:
-
- 9/3 - 5 + 3 × 4
- 9/3 - 5 + 12
- 3 - 5 + 12
- 3 + 7
- Step 10.
-
Part 2 of 5: Understanding the Variables

Step 1. Look for symbols that are not numbers
In algebra, you'll start to see letters and symbols appear in your math problems, not just numbers. These letters and symbols are called variables. Variables aren't as confusing as they may seem at first glance - they're just a way to write down numbers with unknown values. Below are just some common examples of variables in algebra:
- Letters like x, y, z, a, b, and c
- Greek letters like theta or
- Note that not all symbols are unknown variables. For example, pi, or, always equals about 3.1459.

Step 2. Think of variables as "unknown" numbers
As mentioned above, variables are basically just numbers with unknown values. Usually, your goal in algebra problems is to find out the value of a variable - think of the variable as the "mystery number" you're trying to find.
-
For example, in the equation 2x + 3 = 11, x is our variable. This means that there are several values that take up the place of x to make the left side of the equation equal 11. Since 2 × 4 + 3 = 11, in this case, x =
Step 4..
-
An easy way to start understanding variables is to replace them with question marks in algebra problems. For example, we can rewrite the equation 2 + 3 + x = 9 to be 2 + 3 + ?
= 9. This makes it easier for us to understand the things we are trying to do - we just have to find the value that must be added to 2 + 3 = 5 to get 9. Again, of course the answer is
Step 4..

Step 3. If a variable occurs more than once, simplify the variable
What do you do if the same variable appears more than once in an equation? While this situation may seem difficult to solve, you can actually treat variables as you would normal numbers - in other words, you can add them up, subtract them, and so on, as long as you only combine like-like variables. In other words, x + x = 2x, but x + y is not equal to 2xy.
-
For example, let's look at the equation 2x + 1x = 9. In this problem, we can add 2x and 1x to get 3x = 9. Since 3 x 3 = 9, we know that x =
Step 3..
- Note again that you can only add the same variables together. In the equation 2x + 1y = 9, we cannot combine 2x and 1y because they are different variables.
- This also applies when one variable has a different exponent than the other variable. For example, in the equation 2x + 3x2 = 10, we cannot combine 2x and 3x2 because the variable x has a different exponent. See how to add exponents for more information.
Part 3 of 5: Learning How to Solve Equations by "Negating"

Step 1. Try to isolate the variables in the algebraic equations
Solving equations in algebra usually means finding out the value of the variable. Algebraic equations are usually composed of numbers and/or variables on both sides, like this: x + 2 = 9 × 4. To find the value of the variable, you must isolate the variable on one side of the equals sign. Whatever is left on the other side of the equals sign is your answer.
In the example (x + 2 = 9 × 4), to isolate x on the left side of the equation, we need to omit "+ 2". To do this, we just need to subtract 2 from that side, leaving us with x = 9 × 4. However, to keep both sides of the equation equal, we also have to subtract 2 from the other side. This leaves us with x = 9 × 4 - 2. Following the order of operations, we first multiply, then subtract, giving our answer x = = 36 - 2 = 34.

Step 2. Eliminate addition by subtraction (and vice versa)
As we just saw above, excluding x on one side of the equals sign usually means eliminating the numbers next to it. To do this, we perform the "reverse" operation on both sides of the equation. For example, in the equation x + 3 = 0, since we see "+ 3" after our x, we will put "-3" on both sides. "+3" and "-3", leaving x alone and "-3" on the other side of the equals sign, like this: x = -3.
-
In general, addition and subtraction are like "reverses" - calculate one operation to discard the other. See below:
-
- For addition, subtract. Example: x + 9 = 3 → x = 3 - 9
- For subtraction, add up. Example: x - 4 = 20 → x = 20 + 4
-

Step 3. Eliminate multiplication by division (and vice versa)
Multiplication and division are a bit more difficult to work with than addition and subtraction, but these calculations have the same "reverse" relationship. If you see "× 3" on one side, you'll negate it by dividing both sides by 3, and so on.
-
With multiplication and division, you must perform the reverse operation for all numbers on the other side of the equals sign, even if that side contains more than one number. See below:
-
- For multiplication, divide. Example: 6x = 14 + 2→ x = (14 + 2) /6
- For division, multiply. Example: x/5 = 25 → x = 25 × 5
-

Step 4. Remove the exponent by finding the root (and vice versa)
Exponents is a fairly advanced pre-algebra topic - if you don't know how to do it, take a look at our basic exponentials article for more information. The "reverse" of an exponent is a root that has the same number as the exponent. For example, the reciprocal of the exponent 2 is the square root (√), the reciprocal of the exponent 3 is the cube root (3), and so on.
-
This might be a little confusing, but in these cases, you're looking for the roots of both sides when working with an exponent. In other words, you're doing the exponentiation for both sides when you're working with the root. See below:
-
- For the exponent, find the root. Example: x2 = 49 → x = √49
- For roots, raise. Example: x = 12 → x = 122
-
Part 4 of 5: Sharpen Your Algebra Skills

Step 1. Use pictures to make the questions clearer
If you're having trouble imagining an algebra problem, try using a diagram or picture to illustrate your equation. You can even try using a bunch of physical objects (like blocks or coins) if you have one.
-
For example, let's solve the equation x + 2 = 3 using the square (☐)
-
- x +2 = 3
- ☒+☐☐ =☐☐☐
- In this step, we will subtract 2 from both sides by removing 2 squares (☐☐) from both sides:
- ☒+☐☐-☐☐ =☐☐☐-☐☐
-
=☐, or x =
Step 1.
-
-
As another example, let's try 2x = 4
-
- ☒☒ =☐☐☐☐
- In this step, we will divide the two sides by separating the boxes on each side into two groups:
- ☒|☒ =☐☐|☐☐
-
=, or x =
Step 2.
-

Step 2. Use "common sense checks" (especially for story questions)
When converting story problems to algebra, try to check your formulas by entering simple values for your variables. Does your equation make sense when x=0? When x=1? When x= -1? It's easy to make the simple mistake of writing p=6d when you mean p=d/6, but these things will be easy to spot if you do a quick, common sense check on your work before moving on.
For example, we are told that a football field is 30 m longer than it is wide. We use the equation p = l + 30 to represent this problem. We can check if this equation makes sense by entering simple values for l. For example, if the field has a width of l = 10 m, the length is 10 + 30 = 40 m. If the width is 30 m, the length is 30 + 30 = 60 m, and so on. This equation makes sense - we expect this field to have a greater length as the width increases, so this equation makes sense

Step 3. Note that answers are not always integers in algebra
Answers in algebra and other advanced forms are not always simple, round numbers. This number can be a decimal, fractional, or irrational number. A calculator can help you find these complex answers, but remember that your teacher may require you to write your answers in exact form, not in complicated decimal form.
For example, we will simplify an algebraic equation to x = 12507. If we type in 12507 in the calculator, we will get very many decimal places (in addition, because the calculator screen is not very large, the calculator cannot display all the answers.) In this case, we may want to write down our answer as only 12507 or simplify the answer by writing it in scientific notation.

Step 4. When you feel confident with basic algebra, try factoring
One of the most complex algebraic abilities of all is factoring - a kind of shortcut for turning complex equations into simpler forms. Factoring is a semi-advanced algebra topic, so consider consulting the article linked above if you're having trouble mastering it. Below are just a few quick tips for factoring equations:
- The equation of the form ax + ba is factored into a(x + b). Example: 2x + 4 = 2(x + 2)
- Equation of the form ax2 + bx is factored into cx((a/c)x + (b/c)) where c is the largest number that can evenly divide a and b. Example: 3y2 + 12y = 3y(y + 4)
- Equation of the form x2 + bx + c is factored into (x + y)(x + z) where y × z = c and yx + zx = bx. Example: x2 + 4x + 3 = (x + 3)(x + 1).

Step 5. Practice, practice and practice
Progress in algebra (and other types of mathematics) requires a lot of hard work and repetition. Don't worry - by paying attention in class, doing all your assignments, and seeking help from your teacher or other students when you need it, algebra will start to become a habit.

Step 6. Ask your teacher to help you understand complex algebraic topics
If you're having trouble understanding algebra, don't worry - you don't have to learn it alone. Your teacher is the first person you should turn to for questions. After class, politely ask your teacher for help. A good teacher will usually be willing to re-explain the topic of the day in an after-school meeting and your teacher may be able to provide you with additional practice materials.
If, for some reason, your teacher is unable to help you, ask him or her about additional study options at your school. Many schools have some sort of after-school program that can help you get the extra time and attention you need to start mastering your algebra. Remember that using the free help available to you is nothing to be ashamed of - it's a sign that you're smart enough to solve your problem
Part 5 of 5: Exploring Intermediate Topics
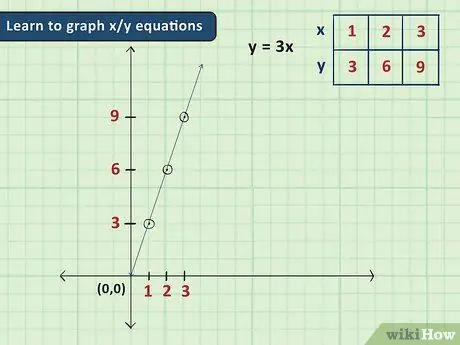
Step 1. Learn how to graph the x/y equation
Graphs can be a valuable tool in algebra because they allow you to present ideas that require numbers in the form of easy-to-understand pictures. Typically, in beginner algebra, graphing problems are limited to equations with two variables (usually x and y) and are represented on simple 2-D graphs with an x-axis and a y-axis. With these equations, all you have to do is enter a value for x, then search for y (or vice versa) to get two numbers that become a point on the graph.
- For example, in the equation y = 3x, if we enter 2 for x, we get y = 6. This means that the point (2, 6) (two steps to the right from the center of the graph and six steps up from the center of the graph) is part of the graph of this equation.
- Equations of the form y = mx + b (where m and b are numbers) are very common in basic algebra. These equations always have a gradient or slope m and intersect the y axis at y = b.

Step 2. Learn how to solve inequalities
What do you do when your equation doesn't have an equal sign? Turns out, not too different from what you usually do. For inequalities, which use signs like > ("greater than") and < ("less than"), just solve as usual. You will leave an answer that is less than or greater than your variable.
-
For example, with the equation 3 > 5x - 2, we would solve it as we would a regular equation:
-
- 3 > 5x - 2
- 5 > 5x
- 1 > x, or x < 1.
-
- This means that any number less than one can be an x value. In other words, x can be 0, -1, -2, and so on. If we plug these numbers into the equation for x, we'll always get an answer that's less than 3.

Step 3. Work on the quadratic equations
One of the algebraic topics that beginners may have trouble with is solving quadratic equations. The square is an equation of the form ax2 + bx + c = 0, where a, b, and c are numbers (except that a cannot be 0). These equations are solved by the formula x = [-b +/- (b2 - 4ac)]/2a. Be careful - the +/- sign means that you have to find answers to addition and subtraction so you can have two answers to these types of questions.
-
For example, let's solve the quadratic formula 3x2 + 2x -1 = 0.
-
- x = [-b +/- (b2 - 4ac)]/2a
- x = [-2 +/- (22 - 4(3)(-1))]/2(3)
- x = [-2 +/- (4 - (-12))]/6
- x = [-2 +/- (16)]/6
- x = [-2 +/- 4]/6
- x = -1 and 1/3
-

Step 4. Experiment with systems of equations
Solving more than one equation at once may sound very complicated, but when you're working with simple algebraic equations, it's actually not that difficult. Often, algebra teachers use a graphical approach to solving these problems. When you're working with a system of two equations, the solutions are the points on the graph where the two equations' lines intersect.
- For example, we are working with a system whose equations are y = 3x - 2 and y = -x - 6. If we draw these two lines on the graph, we will get one line that goes up by a steep angle, and one that goes down by a steep angle. gentle angle. Since these lines intersect at the point (-1, -5), then this point is the solution of this system.
-
If we want to check our problem, we can do so by plugging our answer into the equation in the system - the correct answer will be "correct" for both equations.
-
- y = 3x - 2
- -5 = 3(-1) - 2
- -5 = -3 - 2
- -5 = -5
- y = -x - 6
- -5 = -(-1) - 6
- -5 = 1 - 6
- -5 = -5
-
- Both equations are "checked," so our answer is correct!
Tips
- There are many resources for learning algebra from the internet. For example, search for "algebraic formulas" in a search engine. There are so many great results that will emerge. You can also try browsing through a selection of wikiHow math articles. There's a lot of information out there, so start exploring now!
- One great site for algebra beginners is khanacademy.com. This free site offers dozens of easy-to-follow lessons on a wide variety of topics, including algebra. There are videos for all of these topics, from very easy basics to advanced university-level topics. So don't be afraid to explore Khan Academy's materials and start using all the help the site has to offer!
- Don't forget that your best resources when you're trying to learn algebra include people you know well. Ask your friends or classmates about the last lesson you didn't understand.






