- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-01-23 12:04.
A complex fraction is a fraction in which the numerator, denominator, or both also contain a fraction. For this reason complex fractions are sometimes referred to as "stacked fractions". Simplifying complex fractions can be easy or difficult, depending on how many numbers are in the numerator and denominator, whether one of the numbers is a variable, or the complexity of the variable number. See Step 1 below to get started!
Step
Method 1 of 2: Simplifying Complex Fractions with Inverse Multiplication
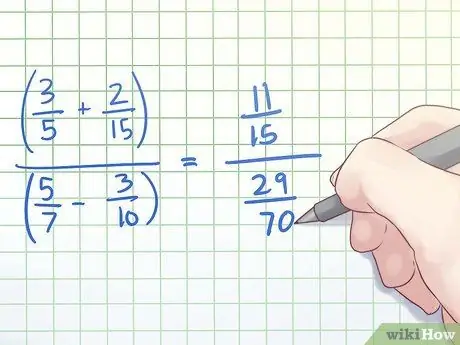
Step 1. Simplify the numerator and denominator to a single fraction if needed
Complex fractions are not always difficult to solve. In fact, complex fractions whose numerator and denominator contain a single fraction are usually fairly easy to solve. So, if the numerator or denominator (or both) of a complex fraction contains multiple fractions or fractions and an integer, simplify it to get a single fraction in both the numerator and denominator. Find the Least Common Multiple (LCM) of two or more fractions.
-
For example, let's say we want to simplify a complex fraction (3/5 + 2/15)/(5/7 - 3/10). First, we will simplify both the numerator and denominator of a complex fraction into a single fraction.
- To simplify the numerator, use the LCM 15 obtained by multiplying 3/5 by and 3/3. The numerator will be 9/15 + 2/15, which equals 11/15.
- To simplify the denominator, we will use the LCM result of 70 which is obtained by multiplying 5/7 by 10/10 and 3/10 by 7/7. The denominator will be 50/70 - 21/70, which equals 29/70.
- Thus, the new complex fraction is (11/15)/(29/70).
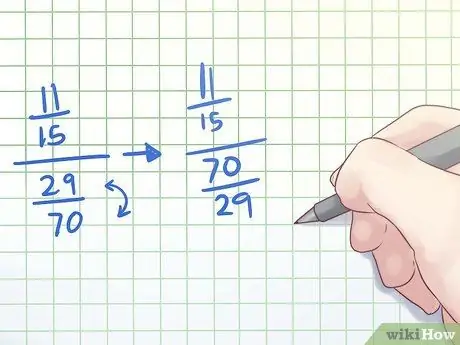
Step 2. Invert the denominator to find its reciprocal
By definition, dividing one number by another is the same as multiplying the first number by the reciprocal of the second number. Now that we have a complex fraction with a single fraction in both the numerator and denominator, we will use this division to simplify the complex fraction. First, find the reciprocal of the fraction at the bottom of the complex fraction. Do this by "inverting" the fraction - putting the numerator in place of the denominator and vice versa.
-
In our example, the fraction in the denominator of the complex fraction (11/15)/(29/70) is 29/70. To find the inverse, we "invert" it so that we get 70/29.
Note that if a complex fraction has an integer in the denominator, we can treat it as a fraction and find its reciprocal. For example, if the complex fraction is (11/15)/(29), we can make the denominator 29/1, which means the reciprocal is 1/29.
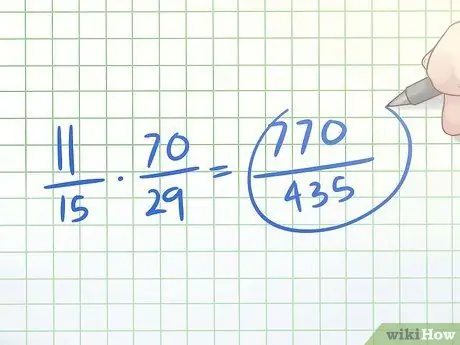
Step 3. Multiply the numerator of the complex fraction by the reciprocal of the denominator
Now that we've got the reciprocal of the denominator of the complex fraction, multiply it by the numerator to get a single simple fraction. Remember that to multiply two fractions, we only cross multiply - the numerator of the new fraction is the number of the numerator of the two old fractions, as well as the denominator.
In our example, we will multiply 11/15 × 70/29. 70 × 11 = 770 and 15 × 29 = 435. So, the new simple fraction is 770/435.

Step 4. Simplify the new fraction by finding the greatest common factor
We already have one simple fraction, so all we have to do is come up with the simplest number. Find the greatest common factor (GCF) of the numerator and denominator and divide both by this number to simplify it.
One of the common factors of 770 and 435 is 5. So, if we divide the numerator and denominator of the fraction by 5, we get 154/87. 154 and 87 have no common factors, so that's the final answer!
Method 2 of 2: Simplifying Complex Fractions Containing Variable Numbers

Step 1. If possible, use the reverse multiplication method above
To be clear, almost all complex fractions can be simplified by subtracting the numerator and denominator by a single fraction and multiplying the numerator by the reciprocal of the denominator. Complex fractions containing variables are also included, although the more complex the expression of variables in complex fractions is, the more difficult and time-consuming it will be to use reverse multiplication. For "easy" complex fractions containing variables, inverse multiplication is a good choice, but complex fractions with multiple variable numbers in the numerator and denominator may be easier to simplify in the alternative way described below.
- For example, (1/x)/(x/6) is easy to simplify by inverse multiplication. 1/x × 6/x = 6/x2. There is no need to use alternative methods here.
- However, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))) is more difficult to simplify by inverse multiplication. Reducing the numerator and denominator of complex fractions to single fractions, multiplying inversely, and reducing the result to the simplest numbers can be a complicated process. In this case, the alternative method below may be easier.

Step 2. If reverse multiplication isn't practical, start by finding the LCM of the fractional number in the complex fraction
The first step is to find the LCM of all the fractional numbers in a complex fraction - both in the numerator and denominator. Usually, if one or more fractional numbers have a number in the denominator, the LCM is the number in the denominator.
This is easier to understand with an example. Let's try to simplify the complex fractions mentioned above, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))). The fractional numbers in this complex fraction are (1)/(x+3) and (1)/(x-5). The LCM of the two fractions is the number in the denominator: (x+3)(x-5).

Step 3. Multiply the numerator of the complex fraction by the newly found LCM
Next, we have to multiply the number in the complex fraction by the LCM of the fractional number. In other words, we will multiply all complex fractions by (KPK)/(KPK). We can do this independently because (KPK)/(KPK) is equal to 1. First, multiply the numerators themselves.
-
In our example, we will multiply the complex fraction, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), i.e. ((x+ 3)(x-5))/((x+3)(x-5)). We have to multiply through the numerator and denominator of the complex fraction, multiplying each number by (x + 3) (x-5).
-
First, let's multiply the numerators: (((1)/(x+3)) + x - 10) × (x+3)(x-5)
- = (((x+3)(x-5)/(x+3)) + x((x+3)(x-5)) - 10((x+3)(x-5))
- = (x-5) + (x(x.)2 - 2x - 15)) - (10(x2 - 2x - 15))
- = (x-5) + (x3 - 2x2 - 15x) - (10x2 - 20x - 150)
- = (x-5) + x3 - 12x2 + 5x + 150
- = x3 - 12x2 +6x+145
-

Step 4. Multiply the denominator of the complex fraction by the LCM as you would with the numerator
Continue multiplying the complex fraction by the LCM found by proceeding to the denominator. Multiply all, multiply each number by the LCM.
-
The denominator of our complex fraction, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), is x +4 +((1) //(x-5)). We will multiply it by the LCM found, (x+3)(x-5).
- (x +4 +((1)/(x - 5))) × (x+3)(x-5)
- = x((x+3)(x-5)) + 4((x+3)(x-5)) + (1/(x-5))(x+3)(x-5).
- = x(x2 - 2x - 15) + 4(x2 - 2x - 15) + ((x+3)(x-5))/(x-5)
- = x3 - 2x2 - 15x + 4x2 - 8x - 60 + (x+3)
- = x3 + 2x2 - 23x - 60 + (x+3)
- = x3 + 2x2 - 22x - 57
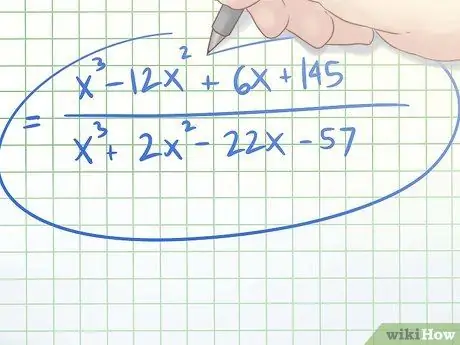
Step 5. Create a new and simplified fraction from the newly found numerator and denominator
After multiplying the fraction by (KPK)/(KPK) and simplifying it by combining the numbers, the result is a simple fraction that does not contain a fractional number. Note that by multiplying by the LCM of the fractional number in the original complex fraction, the denominator of this fraction will be exhausted and leave the variable number and whole number in the answer's numerator and denominator, without any fractions.
With the numerator and denominator found above, we can construct a fraction that is the same as the original complex fraction, but does not contain the fractional number. The numerator that was obtained is x3 - 12x2 + 6x + 145 and the denominator we got was x3 + 2x2 - 22x - 57, so the new fraction becomes (x3 - 12x2 + 6x + 145)/(x3 + 2x2 - 22x - 57)
Tips
- Show every step of the job. Fractions can be confusing if the steps are counting too fast or trying to do it by heart.
- Find examples of complex fractions on the internet or in books. Follow each step until it can be mastered.






