3 Ways to Solve Logarithms

2025 Author: Jason Gerald | [email protected]. Last modified: 2025-01-23 12:04

Logarithms may seem difficult to solve, but solving logarithm problems is actually a lot simpler than you might think, because logarithms are just another way of writing exponential equations. Once you've rewritten the logarithm in a more familiar form, you should be able to solve it like you would any other ordinary exponential equation.

Step

Before You Begin: Learn to Express Logarithmic Equations Exponentially

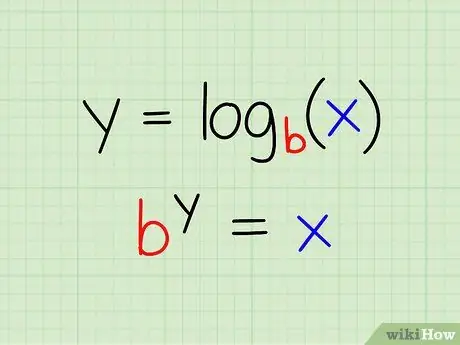
Step 1. Understand the definition of logarithm

Before solving logarithmic equations, you need to understand that logarithms are basically another way of writing exponential equations. The exact definition is as follows:

• y = log_b (x)

  If and only if: b^y = x

• Remember that b is the base of the logarithm. This value must meet the following conditions:

  • b > 0
  • b is not equal to 1
• In the equation, y is the exponent, and x is the result of calculating the exponential sought in the logarithm.

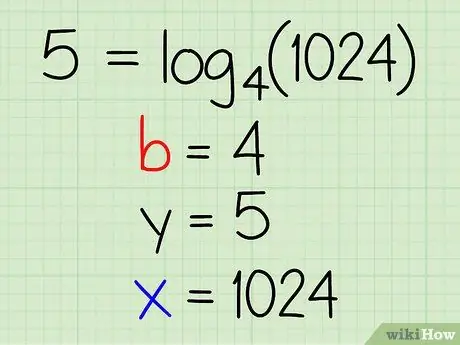
Step 2. Consider the logarithmic equation

When looking at the equation of the problem, look for the base (b), the exponential (y), and the exponential (x).

• Example:

  5 = log₄(1024)

  • b = 4
  • y = 5
  • x = 1024

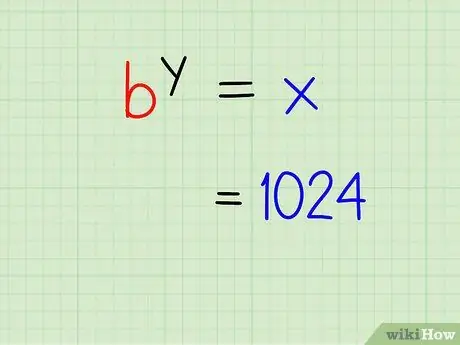
Step 3. Move the exponential to one side of the equation

Move the value of your exponentiation, x, to one side of the equals sign.

• For example:

  1024 = ?

Step 4. Enter the value of the exponent to its base

Your base value, b, must be multiplied by the same number of values represented by the exponent y.

• Example:

  4 * 4 * 4 * 4 * 4 = ?

  This equation can also be written as: 4⁵

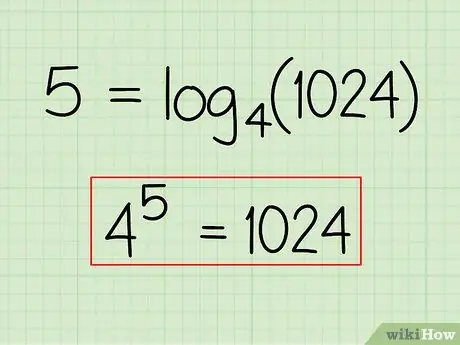
Step 5. Rewrite your final answer

You should now be able to rewrite the logarithmic equation as an exponential equation. Double-check your answer making sure both sides of the equation have the same value.

• Example:

  4⁵ = 1024

Method 1 of 3: Finding the Value of X

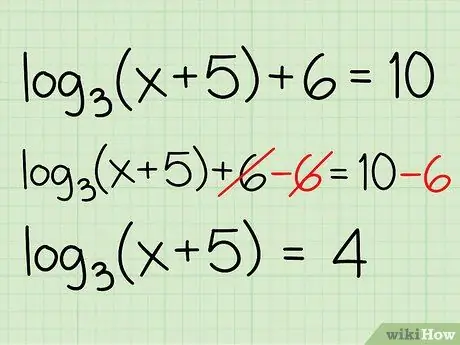
Step 1. Split the logarithmic equation

Perform a reverse calculation to move the part of the equation that is not a logarithmic equation to the other side.

• Example:

  log₃(x + 5) + 6 = 10

  • log₃(x + 5) + 6 - 6 = 10 - 6
  • log₃(x + 5) = 4

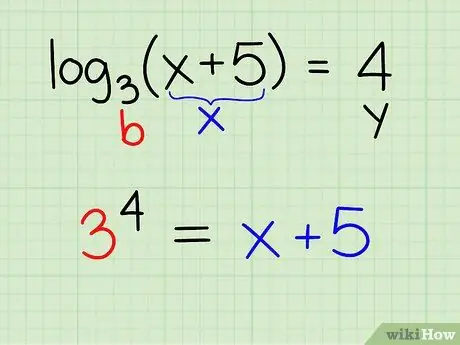
Step 2. Rewrite this equation in exponential form

Use what you already know about the relationship between logarithmic equations and exponential equations, and rewrite them in exponential form that is simpler and easier to solve.

• Example:

  log₃(x + 5) = 4

  • Compare this equation with the definition of [ y = log_b (x)], then you can conclude that: y = 4; b = 3; x = x + 5
  • Rewrite the equation as: b^y = x
  • 3⁴ = x + 5

Step 3. Find the value of x

Once this problem has been simplified to a basic exponential equation, you should be able to solve it just like any other exponential equation.

• Example:

  3⁴ = x + 5

  • 3 * 3 * 3 * 3 = x + 5
  • 81 = x + 5
  • 81 - 5 = x + 5 - 5
  • 76 = x

Step 4. Write down your final answer

The final answer you get when you find the value of x is the answer to your original logarithm problem.

• Example:

  x = 76

Method 2 of 3: Finding the Value of X Using the Logarithmic Addition Rule

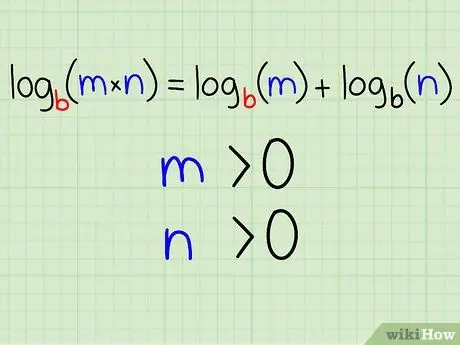
Step 1. Understand the rules for adding logarithms

The first property of logarithms known as the "logarithmic addition rule" states that the logarithm of a product is equal to the sum of the logarithms of the two values. Write this rule in equation form:

• log_b(m * n) = log_b(m) + log_b(n)

• Remember that the following must apply:

  • m > 0
  • n > 0

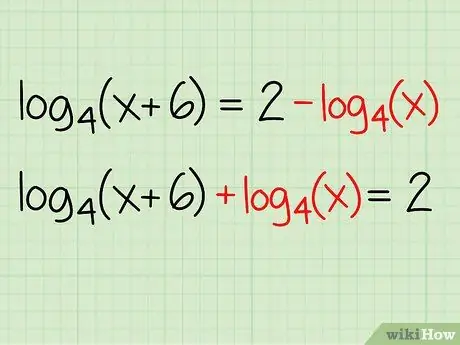
Step 2. Split the logarithm to one side of the equation

Use reverse calculations to move parts of the equation so that the entire logarithmic equation lies on one side, while the other components are on the other side.

• Example:

  log₄(x + 6) = 2 - log₄(x)

  • log₄(x + 6) + log₄(x) = 2 - log₄(x) + log₄(x)
  • log₄(x + 6) + log₄(x) = 2

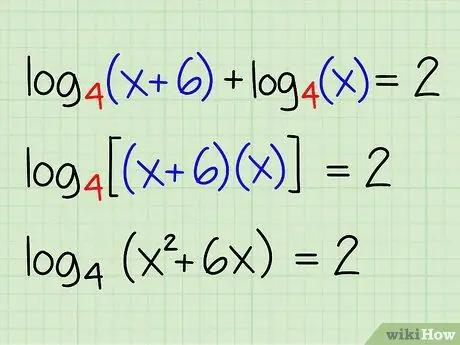
Step 3. Apply the logarithmic addition rule

If two logarithms add up in an equation, you can use the logarithm rule to put them together.

• Example:

  log₄(x + 6) + log₄(x) = 2

  • log₄[(x + 6) * x] = 2
  • log₄(x² + 6x) = 2

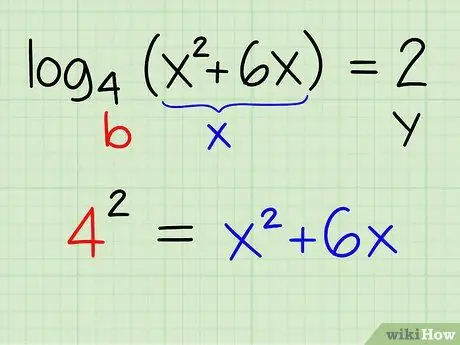
Step 4. Rewrite this equation in exponential form

Remember that logarithms are just another way of writing exponential equations. Use the logarithmic definition to rewrite the equation into a form that can be solved.

• Example:

  log₄(x² + 6x) = 2

  • Compare this equation with the definition of [ y = log_b (x)], you can conclude that: y = 2; b = 4; x = x² + 6x
  • Rewrite this equation so that: b^y = x
  • 4² = x² + 6x

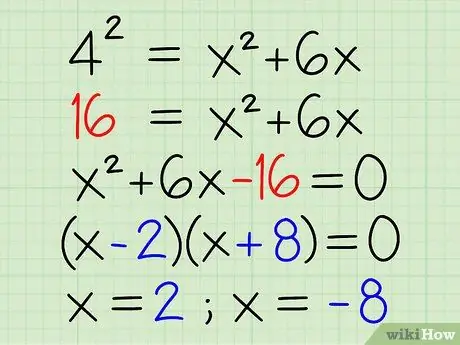
Step 5. Find the value of x

Once this equation has turned into a regular exponential equation, use what you know about exponential equations to find the value of x as you normally would.

• Example:

  4² = x² + 6x

  • 4 * 4 = x² + 6x
  • 16 = x² + 6x
  • 16 - 16 = x² + 6x - 16
  • 0 = x² + 6x - 16
  • 0 = (x - 2) * (x + 8)
  • x = 2; x = -8

Step 6. Write down your answers

At this point, you should have the answer to the equation. Write your answer in the space provided.

• Example:

  x = 2

• Note that you cannot give a negative answer for the logarithm, so you can get rid of the answer x - 8.

Method 3 of 3: Finding the Value of X Using the Logarithmic Division Rule

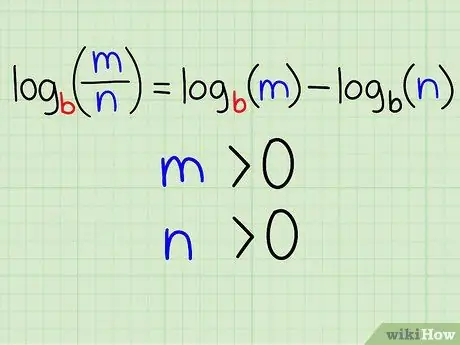
Step 1. Understand the logarithmic division rule

Based on the second property of logarithms, known as the "logarithmic division rule," the logarithm of a division can be rewritten by subtracting the logarithm of the denominator from the numerator. Write this equation as follows:

• log_b(m/n) = log_b(m) - log_b(n)

• Keep in mind that the following must apply:

  • m > 0
  • n > 0

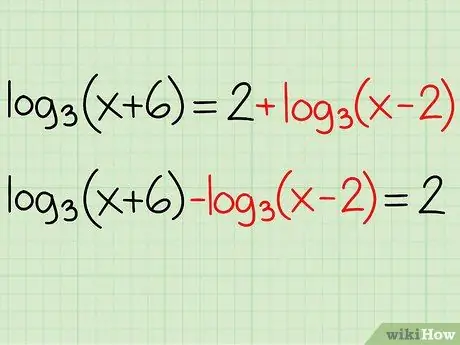
Step 2. Split the logarithmic equation to one side

Before you solve logarithmic equations, you must transfer all logarithmic equations to one side of the equals sign. The other half of the equation must be moved to the other side. Use reverse calculations to solve it.

• Example:

  log₃(x + 6) = 2 + log₃(x - 2)

  • log₃(x + 6) - log₃(x - 2) = 2 + log₃(x - 2) - log₃(x - 2)
  • log₃(x + 6) - log₃(x - 2) = 2

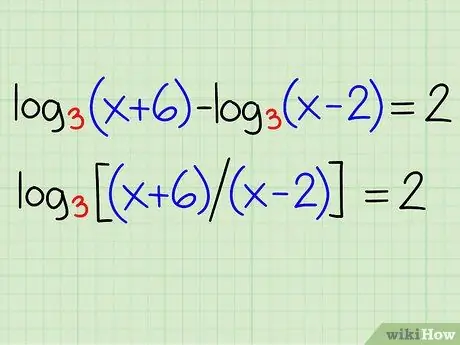
Step 3. Apply the logarithmic division rule

If there are two logarithms in an equation, and one of them must be subtracted from the other, you can and should use the division rule to bring these two logarithms together.

• Example:

  log₃(x + 6) - log₃(x - 2) = 2

  log₃[(x + 6) / (x - 2)] = 2

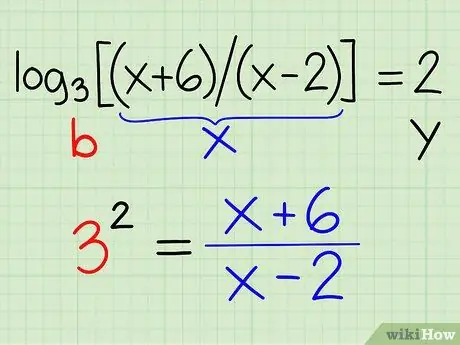
Step 4. Write this equation in exponential form

After only one logarithmic equation remains, use the logarithmic definition to write it in exponential form, eliminating the log.

• Example:

  log₃[(x + 6) / (x - 2)] = 2

  • Compare this equation with the definition of [ y = log_b (x)], you can conclude that: y = 2; b = 3; x = (x + 6) / (x - 2)
  • Rewrite the equation as: b^y = x
  • 3² = (x + 6) / (x - 2)

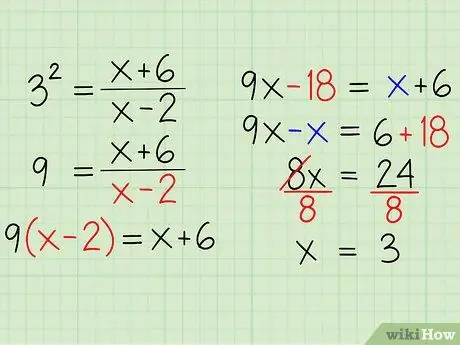
Step 5. Find the value of x

Once the equation is exponential, you should be able to find the value of x as you normally would.

• Example:

  3² = (x + 6) / (x - 2)

  • 3 * 3 = (x + 6) / (x - 2)
  • 9 = (x + 6) / (x - 2)
  • 9 * (x - 2) = [(x + 6) / (x - 2)] * (x - 2)
  • 9x - 18 = x + 6
  • 9x - x - 18 + 18 = x - x + 6 + 18
  • 8x = 24
  • 8x / 8 = 24 / 8
  • x = 3

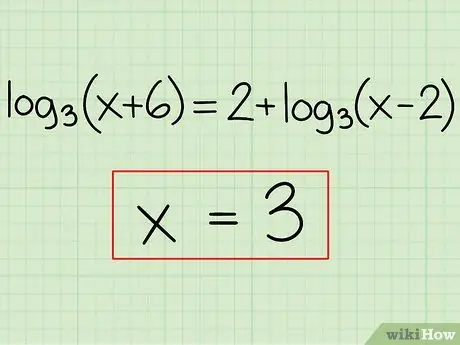
Step 6. Write down your final answer

Research and double-check your calculation steps. Once you are sure that the answer is correct, write it down.

• Example:

  x = 3