LOG (also known as the “compress operator”) is a mathematical medium that compresses numbers. Logarithms are usually used when the numbers are too large or too small to be used easily, as is often the case in astronomy or integrated circuits (ICs). Once compressed, a number can be converted back to its original form using an inverse operator called anti-logarithm.
Step
Method 1 of 2: Using Anti Logarithmic Tables
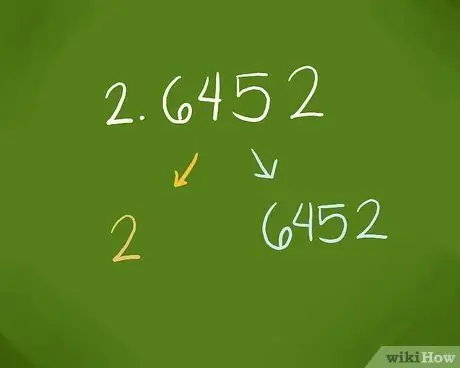
Step 1. Separate the characteristics and the mantissa
Pay attention to the observed numbers. The characteristic is the part that comes before the decimal point; The mantissa is the part that lies after the decimal point. The anti-logarithmic table is structured according to these parameters, so you need to separate them.
For example, suppose you have to find the anti-logarithm for 2.6542. The characteristic is 2, and the mantissa is 6542
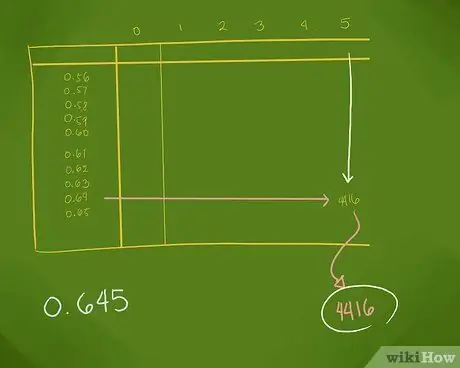
Step 2. Use an anti-logarithmic table to find a suitable value for your mantissa
Anti-logarithmic tables can be searched easily; You may have anti-logarithmic tables in the back of your math textbook. Open the table and look for the number row consisting of the first two digits of the mantissa. Then, look for the column of numbers that matches the third digit of the mantissa.
In the example above, you would open the anti-logarithmic table and look for the row of numbers starting with 0.64, then column 5. In this case, you will find the value is 4416
Step 3. Find the value from the mean difference column
The anti-logarithmic table also includes a set of columns known as the "mean difference column". Look in the same row as before (the row that corresponds to the first two digits of your mantissa), but this time, look for the column number that is the same as the fourth digit of the mantissa.
In the example above, you would return to using a row of numbers starting with 0.64, but looking for the column for 2. In this case, your value is 2
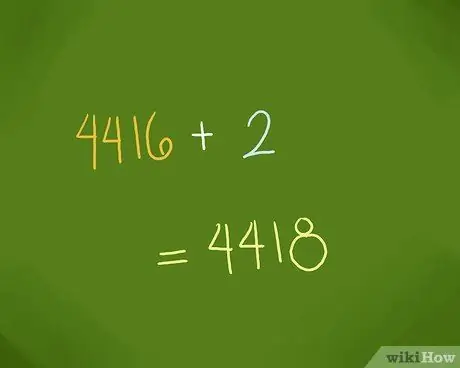
Step 4. Add up the values obtained from the previous step
Once you get these values, the next step is to add them up.
In the example above, you would add 4416 and 2 to get 4418
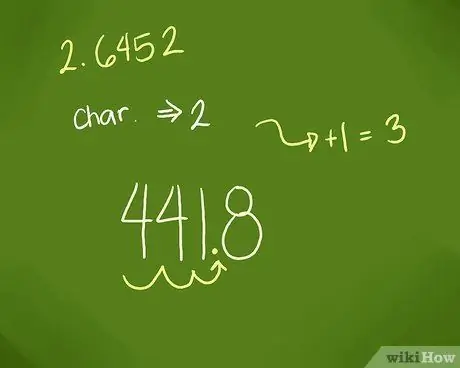
Step 5. Enter the decimal point
The decimal point always lies in a certain specified place: after the number of digits corresponding to the obtained characteristic is added 1.
In the example above, the characteristic is 2. Thus, you would add 2 and 1 to get 3, then enter the decimal point after the 3 digits. Thus, the anti-logarithm of 2.6452 is 441.8
Method 2 of 2: Calculating Anti Logarithms
Step 1. Look at your numbers and their parts
For any number you observe, the characteristic is the part that comes before the decimal point; The mantissa is the part that lies after the decimal point.
For example, suppose you have to find the anti-logarithm of 2, 6452. The characteristic is 2 and the math is 6452
Step 2. Know the base
Mathematical logarithmic operators have a parameter called a base. For numerical calculations, the base is always 10. However, be aware that when you use this method to calculate anti-logarithms, you will always use base 10.
Step 3. Calculate 10^x
By definition, the anti-logarithm of any number x is base^x. Remember that the base for your anti-logarithm is always 10; x is the number you're working with. If the mantissa of the number is 0 (in other words, if the observed number is a whole number, without a decimal point), the calculation is simple: just multiply 10 by 10 several times. If the number is not round, use a computer or calculator to calculate 10^x.
In the example above, we don't have integers. The anti-logarithm is 10^2, 6452, which, using a calculator, would yield 441, 7
Tips
- Logs and anti-logarithms are very often used in scientific and numerical calculations.
- Mathematical operations such as multiplication and division, are easy to calculate in logs. This is because in logarithms, multiplication is converted to addition, and division is converted to subtraction.
- Characteristics and mantissas are just the names of the parts of the number that come before and after the decimal point. Both have no special meaning.
