Dividing fractions by whole numbers is not as difficult as it seems. To divide a fraction by an integer, all you have to do is convert the whole number to a fraction, find the reciprocal of the fraction, and multiply the result by the first fraction. If you want to know how to do it, just follow these steps:
Step
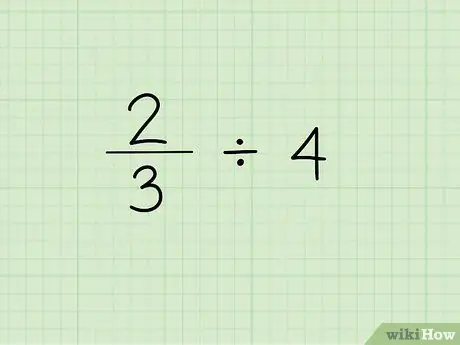
Step 1. Write down the problem
The first step to dividing a fraction by an integer is to write the fraction followed by the divide sign and the integer you need to divide the fraction. Let's say we are working with the following problem: 2/3 4.
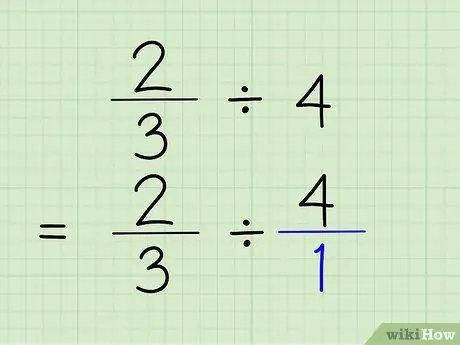
Step 2. Convert integers to fractions
To convert an integer to a fraction, all you have to do is place the integer above the number 1. The integer becomes the numerator and 1 becomes the denominator of the fraction. Saying 4/1 is really the same as saying 4, because you're only showing that the number contains "1" 4 times. The problem will be 2/3 4/1.
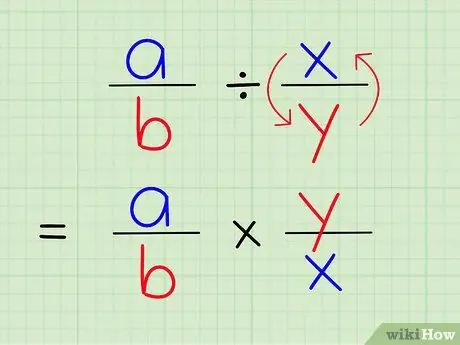
Step 3. Dividing one fraction by another is the same as multiplying that fraction by the reciprocal of another fraction
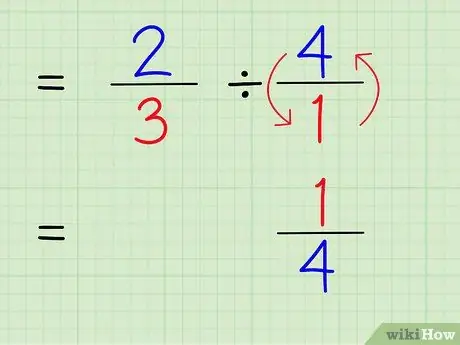
Step 4. Write the reciprocal of the integer
To find the reciprocal of a number, swap the numerator and denominator of the number. Therefore, to find the reciprocal of 4/1, just swap the numerator and denominator so that the number becomes 1/4.
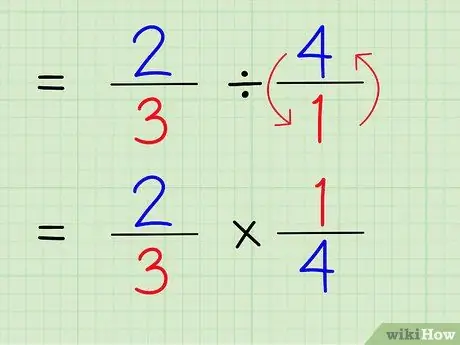
Step 5. Change the division sign to the multiplication sign
The problem will be 2/3 x 1/4.
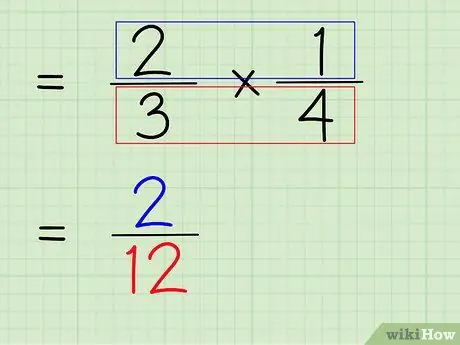
Step 6. Multiply the numerator and denominator of the fraction
So, the next step is to multiply the numerator and denominator of the fraction to get a new numerator and denominator as the final answer.
- To multiply the numerators, just multiply 2 x 1 to get 2.
- To multiply the denominators, just multiply 3 x 4 to get 12.
- 2/3 x 1/4 = 2/12
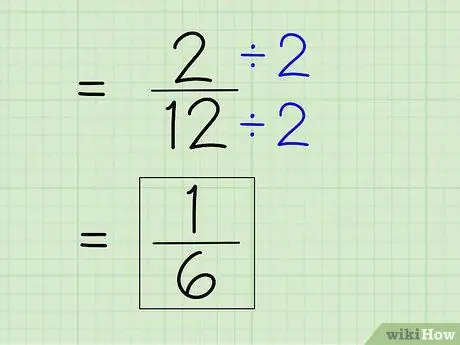
Step 7. Simplify the fraction
To simplify fractions, you must find the smallest denominator, which means that you must divide the numerator and denominator by any number that divides both numbers. Since 2 is the numerator, you have to see if 2 can divide 12 completely -- it can because 12 is an even number. Then, divide the numerator and denominator by 2 to get a new numerator and denominator to get a simple answer.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- The fraction 2/12 can be simplified to 1/6. This is your final answer.
Tips
- This is to aid memory, an easy way to remember how to do all these calculations. Keep this in mind: "It's easy to divide fractions, reverse the second number and multiply!"
- Another variation of the above method is JGB/JBG. Don't change the first number. Change to multiplication. Reverse the last number. Or B first then G.
- If you cancel the calculation before you multiply it, you may not need to find the simplest form of the fraction because the result is already in the simplest fraction form as you can see. In our example, before we multiply 2/3 × 1/4, we can see that the first numerator (2) and the second denominator (4) have the same multiplier of 2, which we can cancel before we continue the calculation. This converts the problem to 1/3 × 1/2, which gives an immediate 1/6 result and saves us time simplifying the fraction at a later stage.
- If one of your fractions is negative, this method is still workable; make sure you keep track of the signs as you perform these steps.
