- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
In mathematics, factoring is a way of finding numbers or expressions which when multiplied will produce a given number or equation. Factoring is a useful skill to learn to solve simple algebra problems; the ability to factor well, becomes important when dealing with quadratic equations and other forms of polynomials. Factoring can be used to simplify algebraic expressions to make their solutions easier. Factoring can even give you the ability to eliminate certain possible answers, much faster than solving them manually.
Step
Method 1 of 3: Factoring Numbers and Simple Algebraic Expressions

Step 1. Understand the definition of factoring when applied to single numbers
Factoring is a simple concept, but in practice, it can be challenging when applied to complex equations. Therefore, it is easiest to approach the concept of factoring by starting with simple numbers, then proceeding to simple equations, before finally moving on to more complex applications. Factors of a number are numbers which when multiplied produce the number. For example, the factors of 12 are 1, 12, 2, 6, 3, and 4, because 1 × 12, 2 × 6, and 3 × 4 are equal to 12.
- Another way to think of it is that the factors of a number are numbers that can divide evenly into the number.
-
Can you find all the factors of the number 60? We use the number 60 for various purposes (minutes in an hour, seconds in a minute, etc.) because it is divisible by quite a lot of other numbers.
The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60

Step 2. Understand that variable expressions can also be factored
Just as numbers themselves can be factored, variables with number coefficients can also be factored. To do this, just find the factors of the variable coefficients. Knowing how to factor a variable is very useful for simplifying algebraic equations involving that variable.
-
For example, the variable 12x can be written as the product of the factors 12 and x. We can write 12x as 3(4x), 2(6x), etc., using whichever factors of 12 work best for our purposes.
We can even factor 12x multiple times. In other words, we don't have to stop at 3(4x) or 2(6x) - we can factor 4x and 6x to produce 3(2(2x) and 2(3(2x). Of course, these two expressions are equivalent

Step 3. Apply the distributive property of multiplication to factor algebraic equations
Using your knowledge of how to factor both single numbers and variables with coefficients, you can simplify simple algebraic equations by finding the factors that numbers and variables share in algebraic equations. Usually, to simplify an equation, we try to find the greatest common factor. This simplification process is possible because of the distributive property of multiplication, which applies to any number a, b, and c. a(b + c) = ab + ac.
- Let's try an example question. To factorize the algebraic equation 12x + 6, first, let's try to find the greatest common factor of 12x and 6. 6 is the largest number that can evenly divide 12x and 6, so we can simplify the equation to 6(2x + 1).
- This process also applies to equations with negative numbers and fractions. For example, x/2 + 4, can be simplified to 1/2(x + 8), and -7x + -21 can be factored to -7(x + 3).
Method 2 of 3: Factoring Quadratic Equations

Step 1. Make sure that the equation is in quadratic form (ax2 + bx + c = 0).
Quadratic equations have the form ax2 + bx + c = 0, where a, b, and c are number constants and not equal to 0 (note that a can equal 1 or -1). If you have an equation that has one variable (x) that has one term x to the power of two or more, you usually move these terms in the equation using simple algebraic operations to get 0 on either side of the equals sign and ax2, etc. on the other.
- For example, let's think of an algebraic equation. 5x2 + 7x - 9 = 4x2 + x - 18 can be simplified to x2 + 6x + 9 = 0, which is the square form.
- Equations with the larger power of x, such as x3, x4, etc. are not quadratic equations. These equations are cubic equations, to the fourth power, and so on, unless the equation can be simplified to remove these x terms with powers greater than 2.

Step 2. In a quadratic equation, where a = 1, factor into (x+d)(x+e), where d × e = c and d + e = b
If your quadratic equation is in the form x2 + bx + c = 0 (in other words, if the coefficient of the term x2 = 1), it is possible (but not guaranteed) that a fairly easy shorthand method can be used to factor the equation. Find two numbers which when multiplied give c and added together to produce b. After you've searched for these two numbers d and e, put them in the following expression: (x+d)(x+e). These two terms, when multiplied, give you your quadratic equation - in other words, they are the factors of your quadratic equation.
- For example, let's think of the quadratic equation x2 + 5x + 6 = 0. 3 and 2 are multiplied to make 6 and also added to give 5, so we can simplify this equation to (x + 3)(x + 2).
-
The slight difference in this basic short method lies in the differences in the similarities themselves:
- If the quadratic equation is in the form x2-bx+c, your answer is in this form: (x - _)(x - _).
- If the equation is in the form x2+bx+c, your answer looks like this: (x + _)(x + _).
- If the equation is in the form x2-bx-c, your answer is in the form (x + _)(x - _).
- Note: the numbers in the blanks can be fractions or decimals. For example, the equation x2 + (21/2)x + 5 = 0 is factored into (x + 10)(x + 1/2).

Step 3. If possible, factor through checks
Believe it or not, for uncomplicated quadratic equations, one of the allowed factoring methods is to examine the problem, then consider the possible answers until you find the correct answer. This method is also known as factoring through examination. If the equation is in the form ax2+bx+c and a>1, your factor answer is of the form (dx +/- _)(ex +/- _), where d and e are constants of nonzero numbers which when multiplied gives a. Neither d nor e (or both) can be 1, although it doesn't have to be. If both are 1, you're basically using the shorthand method described above.
Let's think of an example problem. 3x2 - 8x + 4 looks difficult at first. However, once we realize that 3 has only two factors (3 and 1), this equation becomes easier because we know that our answer must be of the form (3x +/- _)(x +/- _). In this case, adding -2 to both blanks gives the correct answer. -2 × 3x = -6x and -2 × x = -2x. -6x and -2x add up to -8x. -2 × -2 = 4, so we can see that the terms factored in parentheses when multiplied produce the original equation.

Step 4. Solve by completing the square
In some cases, quadratic equations can be quickly and easily factored using special algebraic identities. Any quadratic equation in the form x2 + 2xh + h2 = (x + h)2. So if in your equation your b value is twice the square root of your c value, your equation can be factored to (x + (root(c)))2.
For example, the equation x2 +6x+9 has this shape. 32 is 9 and 3 × 2 is 6. So, we know that the factor form of this equation is (x + 3)(x + 3), or (x + 3)2.
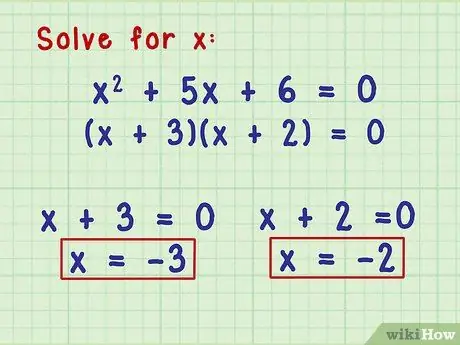
Step 5. Use factors to solve quadratic equations
Regardless of how you factored your quadratic equation, once the equation is factored, you can find possible answers to the value of x by making each factor equal to zero and solving them. Since you are looking for the value of x that makes your equation equal to zero, the value of x that makes any factor equal to zero is a possible answer to your quadratic equation.
Let's go back to equation x2 + 5x + 6 = 0. This equation is factored into (x + 3)(x + 2) = 0. If either factor equals 0, all equations equal 0, so our possible answers for x are numbers- a number that makes (x + 3) and (x + 2) equal 0. These numbers are -3 and -2, respectively.

Step 6. Check your answers - some of the answers may be misleading
When you find possible answers for x, plug them back into your original equation to see if the answer is correct. Sometimes, the answers you find don't make the original equation equal to zero when re-entered. We call this answer deviant and ignore it.
-
Let's put -2 and -3 into x2 + 5x + 6 = 0. First, -2:
- (-2)2 + 5(-2) + 6 = 0
- 4 + -10 + 6 = 0
- 0 = 0. This answer is correct, so -2 is the correct answer.
-
Now, let's try -3:
- (-3)2 + 5(-3) + 6 = 0
- 9 + -15 + 6 = 0
- 0 = 0. This answer is also correct, so -3 is the correct answer.
Method 3 of 3: Factoring Other Equations

Step 1. If the equation is expressed in the form a2-b2, factor into (a+b)(a-b).
Equations with two variables have different factors than the basic quadratic equation. For equation a2-b2 anything where a and b are not equal to 0, the factors of the equation are (a+b)(a-b).
For example, the equation 9x2 - 4y2 = (3x + 2y)(3x - 2y).

Step 2. If the equation is expressed in the form a2+2ab+b2, factor into (a+b)2.
Note that, if the trinomial is of the form a2-2ab+b2, the form factors are slightly different: (a-b)2.
4x. equation2 + 8xy + 4y2 can be rewritten as 4x2 + (2 × 2 × 2)xy + 4y2. Now, we can see that the form is correct, so we can be sure that the factors of our equation are (2x + 2y)2

Step 3. If the equation is expressed in the form a3-b3, factor into (a-b)(a2+ab+b2).
Finally, it was already mentioned that cubic equations and even higher powers, can be factored, although the factoring process quickly becomes very complicated.
For example, 8x3 - 27y3 factored into (2x - 3y)(4x2 + ((2x)(3y)) + 9y2)
Tips
- a2-b2 can be factored, a2+b2 cannot be factored.
- Remember how to factor a constant. This might help.
- Be careful with fractions in the factoring process and work with fractions correctly and carefully.
- If you have a trinomial of the form x2+bx+ (b/2)2, the form factor is (x+(b/2))2. (You may encounter this situation when completing the square.)
- Remember that a0=0 (the property of the product of zero).






