- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-06-01 06:05.
Two-step algebra is relatively quick and easy - because it only takes two steps. To solve a two-step algebraic equation, all you have to do is isolate the variables using addition, subtraction, multiplication, or division. If you want to know how to solve two-step algebraic equations in different ways, just follow these steps.
Step
Method 1 of 3: Solving Equations with One Variable
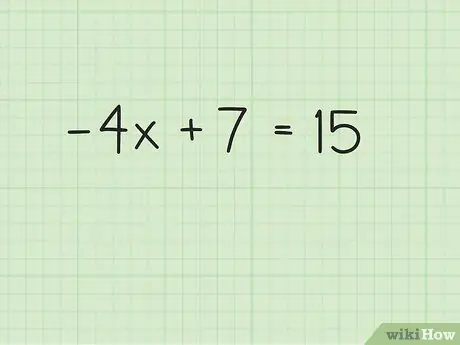
Step 1. Write down the problem
The first step to solving a two-step algebraic equation is to write down the problem so you can imagine the answer. Suppose you want to solve this problem: -4x + 7 = 15.

Step 2. Decide if you want to use addition or subtraction to isolate the variable
The next step is to figure out how to get -4x on one side and the constants (whole numbers) on the other. To do this, you have to do Inverse Addition, finding the reciprocal of +7, which is -7. Subtract 7 from both sides of the equation so that +7, which is on the same side as the variable, disappears. Just write -7 under the number 7 on one side and under 15 on the other so that the equation remains equal.
Remember the Great Rules of Algebra. You have to do the same on both sides to balance the equation. That's the reason why 15 is also reduced by 7. We only need to subtract 7 once on each side, so -4x doesn't need to be subtracted by 7
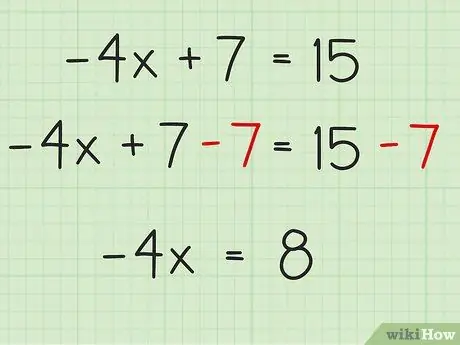
Step 3. Add or subtract the constants on both sides of the equation
This will isolate the variable. Subtracting 7 from +7 on the left side of the equation removes the constant on the left side of the equation. Subtracting 7 from +15 on the right side of the equation will give you the number 8. Thus, the new equation is -4x = 8.
- -4x + 7 = 15 =
- -4x = 8
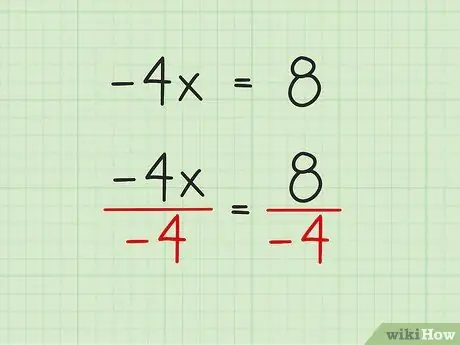
Step 4. Eliminate variable coefficients through division or multiplication
Coefficient is a number that is tied to a variable. In this example, the coefficient is -4. To remove -4 from -4x, you must divide both sides of the equation by -4. In this problem, x is multiplied by -4, so the reverse of this operation is division and you have to divide both sides.
Again, you have to do the same on both sides. That's why you see -4 twice
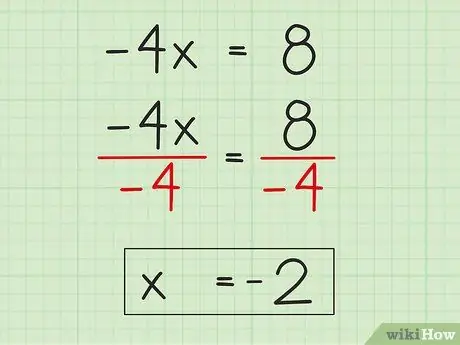
Step 5. Find the value of the variable
To do this, divide the left side of the equation, -4x, by -4, making it x. Divide the right side of the equation, 8, by -4, making it -2. Thus, x = -2. You've already done two steps - subtraction and division - to solve this equation.
Method 2 of 3: Solving Equations with One Variable on Each Side

Step 1. Write down the problem
The problem you will be working on is: -2x - 3 = 4x - 15. Before you continue, make sure that the two variables are equal. In this case, -2x and 4x have the same variable, which is x, so you can move on to the next step.
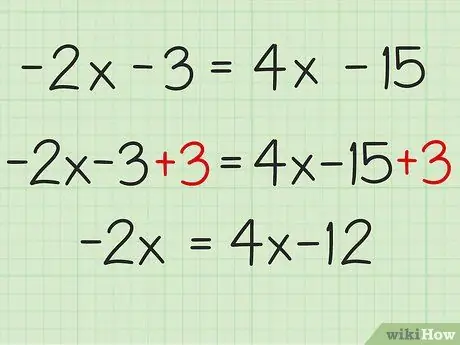
Step 2. Move the constant to the right side of the equation
To do this, you must add or subtract to remove the constant from the left side of the equation. The constant is -3, so you have to find its reciprocal, which is +3, and add this constant to both sides of the equation.
- Adding +3 to the left side of the equation, -2x-3, will result in (-2x -3) + 3 or -2x on the left.
- Adding +3 to the right side of the equation, 4x -15, gives (4x - 15) +3 or 4x -12.
- Thus, (-2x - 3) +3 = (4x - 15) +3 = -2x = 4x - 12
- The new equation becomes -2x = 4x -12

Step 3. Move the variable to the left side of the equation
To do this, you just need to find the reciprocal of 4x, which is -4x and subtract -4x from both sides of the equation. On the left, -2x - 4x = -6x, and on the right, (4x -12) -4x = -12, so the new equation becomes -6x = -12
2x - 4x = (4x - 12) - 4x = -6x = -12
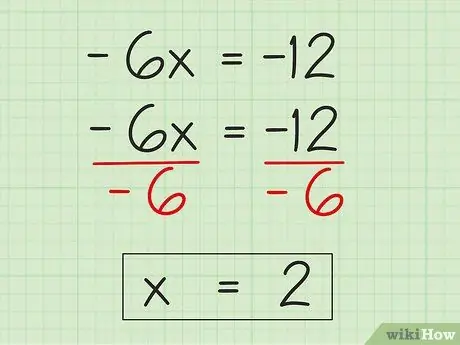
Step 4. Find the value of the variable
Now that you've simplified the equation to -6x = -12, all you have to do is divide both sides of the equation by -6 to isolate the variable x, which is now multiplied by -6. On the left side of the equation, -6x -6 = x, and on the right side of the equation, -12 -6 = 2. Thus, x = 2.
- -6x -6 = -12 -6
- x = 2
Method 3 of 3: Other Ways to Solve Two-Step Equations

Step 1. Solve the two-step equation while keeping the variable on the right
You can solve a two-step equation while keeping the variables on the right side. As long as you isolate it, you will get the same result. For example, 11 = 3 - 7x. To solve this, your first step is to combine the constants by subtracting 3 from both sides of the equation. Then, you have to divide both sides of the equation by -7 to get the x value. Here's how you do it:
- 11 = 3 - 7x =
- 11 - 3 = 3 - 3 - 7x =
- 8 = - 7x =
- 8/-7 = -7/7x
- -8/7 = x or -1.14 = x

Step 2. Solve the two-step equation by multiplying in the last step instead of dividing
The principle of solving equations like this is always the same: use arithmetic to combine constants, isolate variables, and then isolate variables without coefficients. Suppose you want to solve the equation x/5 + 7 = -3. The first step you have to do is to subtract 7 on both sides, add -3, and then multiply both sides by 5 to find the x value. Here's how you do it:
- x/5 + 7 = -3 =
- (x/5 + 7) - 7 = -3 - 7 =
- x/5 = -10
- x/5 * 5 = -10 * 5
- x = -50
Tips
- When multiplying or dividing two numbers with different signs (for example, one positive and the other negative), the result is always negative. If both signs are equal, then the answer is a positive number.
- If there is no number in front of x, assume it is 1x.
- Constants don't always have to be on each side. If no number follows x, assume it is x+0.






