Cross multiplication is a way to solve equations involving a variable of two equivalent fractions. A variable is a placeholder for an unknown quantity of numbers and cross multiplication turns it into a simple equation, allowing you to find the value of the variable in question. Cross multiplication is very useful when you want to complete a comparison. Here's how to do it:
Step
Method 1 of 2: Cross Product of One Variable
Step 1. Multiply the numerator of the left fraction by the denominator of the right fraction
Say you want to solve the equation 2/x = 10/13. Now, multiply 2 by 13.2 x 13 = 26.
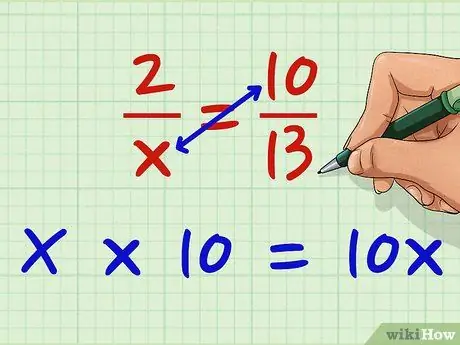
Step 2. Multiply the right fraction's numerator by the left's denominator
Multiply x by 10. X * 10 = 10x. You can cross this section first; it doesn't matter as long as you multiply both numerators by both denominators diagonally.
Step 3. Make the two products equal
26 is equivalent to 10x. 26 = 10x. It doesn't matter which one is on the right or left; being equal, you can change their location as long as you move them all at once.
So if you try to find the x value of 2/x = 10/13, 2 * 13 = x * 10 or 26 = 10x
Step 4. Find the value of the variable
Now that you have 26 = 10x, you can try to find a common numerator and divide 26 and 10 by the same number that divides both. Since both are even numbers, you can divide by 2; 26/2 = 13 and 10/2 = 5. The remainder is 13 = 5x. Now, taking x apart, divide both sides of the equation by 5. So 13/5 = 5/5 or 13/5 = x. If you want the answer in decimal form, you can start by dividing both sides of the equation by 10 to get 26/10 = 10/10 or 2,6 = x.
Method 2 of 2: Multivariable Cross Multiplication
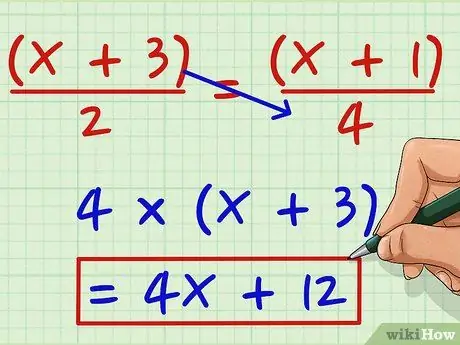
Step 1. Multiply the numerator on the left by the denominator on the right
Say you want to solve the following equation: (x + 3)/2 = (x + 1)/4. Multiply (x + 3) by 4 to get 4(x + 3). Multiply by 4 to get 4x + 12.
Step 2. Multiply the numerator on the right by the denominator on the left
Repeat the process on the other side. (x+1) x 2 = 2(x+1). Multiply by 2 to get 2x + 2.
Step 3. Make the product of the two equal and combine the same variables
Now, the result is 4x + 12 = 2x + 2. Combine the variable x and the constant on the other side of the equation.
- So, combine 4x and 2x by subtracting 2x from both sides. Subtracting 2x from 2x will leave a remainder of 0. On the left, 4x – 2x = 2x, so the remainder is 2x.
- Now, combine 12 and 2 by subtracting 12 from both sides. Subtract 12 from 12 on the left side and the result is 0, then subtract 12 from 2 on the right side so that the result is 2 – 12 = -10.
- The remainder is 2x = -10.
Step 4. Finish
All you have to do is divide both sides of the equation by 2. 2x/2 = -10/2 = x = -5. After cross multiplying, you find that x = -5. You can go back and check your work by entering the value of x, which is -5 to make sure both sides are equal. It turned out to be equivalent. If you plug -5 into the original equation, the result is -1 = -1.
Tips
- Note that if you plug different numbers (say 5) into the same equation, the result is 2/5 = 10/13. Even if you multiply the left side by another 5/5, you get 10/25 = 10/13, which is clearly wrong. This case indicates that you made a cross multiplying error.
- You can check your answer by plugging your result into the original equation. If the equation is a true statement, for example 1 = 1, your answer is correct. If the equation becomes a false statement, for example 0 = 1, you are making a mistake. For example, plug 2, 6 into the equation so that 2/(2, 6) = 10/13. Multiply the left side by 5/5 to get 10/13 = 10/13. The result is a correct statement, which when simplified becomes 1 = 1, so 2, 6 is the correct answer.
