- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-06-01 06:05.
Multiplying lengths can seem a little daunting, especially if you're multiplying two numbers that are rather large. However, if you do it step by step, you will be able to complete long multiplications quickly. Get ready to complete those math quizzes by seeing Step 1 below to get started.
Step
Method 1 of 2: Performing Ordinary Long Multiplication
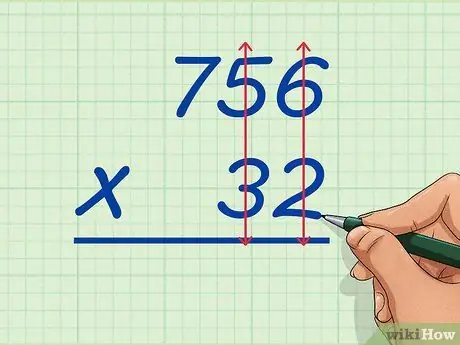
Step 1. Write the big number over the small number
For example, you will multiply 756 and 32. Write 756 over 32, making sure that the ones and tens values of the two numbers align, so that the 6 of 756 is above the 2 of 32 and the 5 of 756 is above the 3 of 32, and so on.. This will make it easier for you to imagine the long multiplication process.
Basically, you'll start multiplying 2 of 32 by all 756, and then multiplying 3 of 32 by all 756. But don't do that just yet
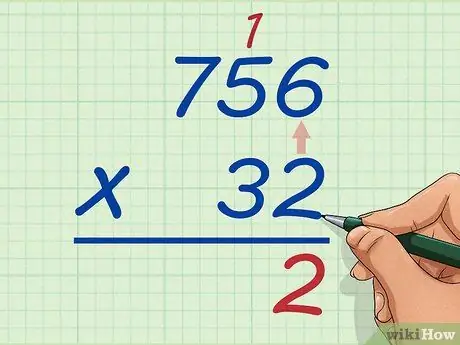
Step 2. Multiply the units digit of the bottom number by the units digit of the top number
Take 2 of 32 and multiply it by 6 of 756. The product of 6 and 2 is 12. Write the units digit, 2, under the ones place, and move 1 above the 5. Basically, you write whatever the product is in the ones place, and if there is a number in the tens place, you have to move it above the number to the left of the top number you just multiplied. You have 2 under 6 and 2.

Step 3. Multiply the ones digit from the bottom number by the tens digit from the top number
Now multiply 2 and 5 by 10. Add the 1 you wrote above 5 to 10 to make it 11, and then write the 1 next to the 2 in the answer section. You must move the number 1 in the tens place above 7.

Step 4. Multiply the ones digit from the bottom number by the hundreds from the top number
Now, multiply 2 by 7 to equal 14. Then add the 1 you wrote down to 14 so that it becomes 15. Don't move the tens value, because there are no more multiplied numbers for this row. Just write 15 in the answer section.
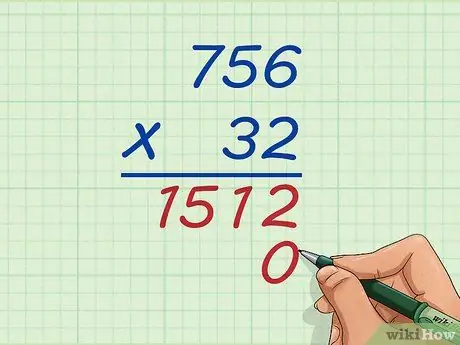
Step 5. Write 0 in the units column below the first multiplication answer
Now, you're going to be multiplying the tens digit of 32, which is 3, by all 756, so write a 0 under the 2 of 1512 before starting to multiply because you're starting from the tens place. If you're going to multiply the hundreds by the top digit, you have to write down two zeros, and so on.
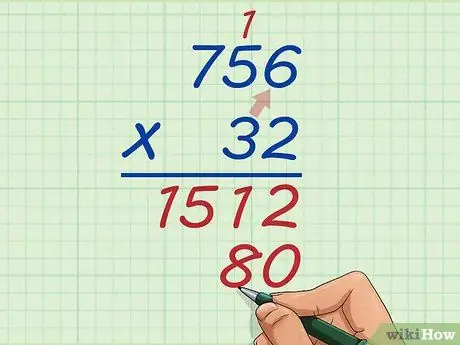
Step 6. Multiply the tens digit from the bottom number by the ones digit from the top number
Now multiply 3 by 6 equals 18. Again, place the 8 next to the 0, and move the 1 over 5.

Step 7. Multiply the tens number from the bottom number by the tens number from the top number
Multiply 3 by 5. The result is 15, but you have to add the 1 that was written earlier, so that it becomes 16. Write the number 6 in the answer section, and move the number 1 over 7.

Step 8. Multiply the tens number from the bottom number by the hundreds from the top number
Multiply 3 by 7 equals 21. Add the number 1 written earlier so that it becomes 22. You don't need to move the tens number 2 from 22 because there are no more numbers that can be multiplied, so you can write it directly next to the number 6.
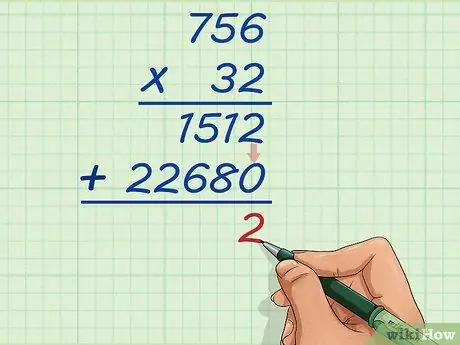
Step 9. Add up the unit values of the two multiplication results
Now you just need to add 1512 and 22680. First, add 2 with 0 equals 2. Write the result in the units column.

Step 10. Add up the second tens of the product
Now, adding up 1 and 8 equals 9. Write 9 to the left of the number 2.

Step 11. Add up the second hundreds of multiplication results
The sum of 5 and 6 is 11. Write the number 1 in the ones place and move the tens number 1 above the 1 which is on the far left of the first product.

Step 12. Add up the thousands of the two multiplication results
Add up 1 with 2 equals 3 and then add up the number 1 you wrote earlier so that it becomes 4. Write it down.
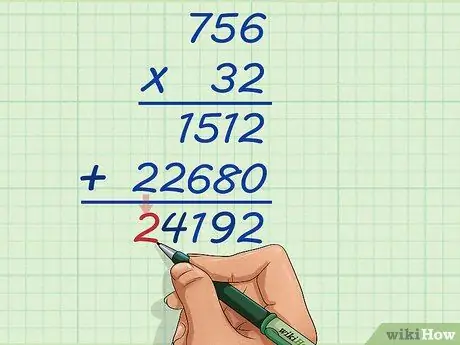
Step 13. Add up the tens of thousands of the two multiplication results
The first number does not have the value of tens of thousands, and the second number has the value of 2. So, add up 0 and 2 to make 2 and write it down. Your final answer will be 24,192.

Step 14. Check your answers using a calculator
If you want to double-check your work, use a calculator to check your answers. Supposedly, 756 times 32 equals 24,192. You're done with it!
Method 2 of 2: Shorten Multiplication

Step 1. Write down the problem
Suppose you are going to multiply 325 by 12. Write it down. One number must be to the right of the other number, not below it.

Step 2. Divide the smaller number into tens and ones
Leave the number 325 alone and divide 12 into 10 and 2. The 1 is in the tens place so you always have to add 0 after dividing, and since 2 is in the ones place, you can just write down the number 2.

Step 3. Multiply the large number by the number in the tens place
Now, multiply 325 by 10. All you have to do is add a zero at the end, so the result is 3250.

Step 4. Multiply the large number by the number in the ones place
Now, multiply 325 by 2. You can imagine that and get 650 because 300 times 2 equals 600 and 25 times 2 equals 50. Add up 600 and 50 to make 650.
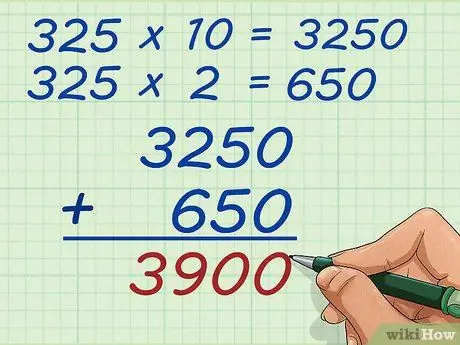
Step 5. Add the two products together
Now, just add up 3250 and 650. You can add them up using the old-fashioned addition method. Write 3250 over 650 and do the addition. You will get 3,900 results. This is the same as the regular long multiplication method, but dividing a number into tens and ones values lets you visualize them and avoids multiplying and moving numbers too much. Either way will yield the same result, and it's up to you which way is faster for you.
Tips
- Practice with short, easy numbers first.
- Make sure you enter your numbers in the correct column!
- Don't forget to move your tens value, otherwise the result will be wrong.
- Always put a 0 at the end of the tens. In hundreds put TWO 0's and so on. Also, check your work carefully and use a calculator to check - but don't use a calculator to calculate answers.
- For numbers with more than 2 digits, follow these steps: first multiply the number above by the units, then add zero and multiply by tens, then add two zeros and multiply by hundreds, then add three zeros and multiply by thousands, and so on. Add up all the numbers.






