- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-01-23 12:04.
To calculate the area of a triangle, you need to know its height. If this data is unknown in the problem, you can easily calculate it based on the known data. This article will guide you through finding the height of a triangle using three different methods, based on known data.
Step
Method 1 of 3: Using Base and Area to Find Height

Step 1. Recall the formula for the area of a triangle
The formula for the area of a triangle is L=1/2at.
- L = area of triangle
- a = length of the base of the triangle
- t = height of triangle from base
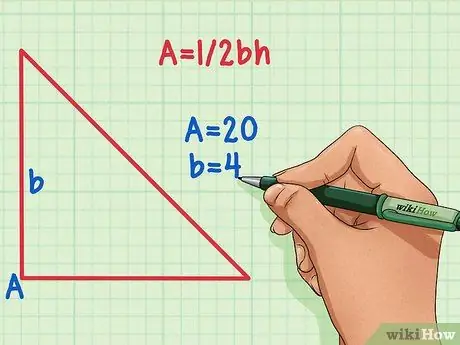
Step 2. Look at the triangle in the problem and determine which variables are known
In the method here, the area of the triangle is known, so enter that value as a variable L. You should also know the length of one of the sides, enter that value as a variable a. If you don't know the area and base of the triangle, you'll have to use another method of calculation.
- Regardless of the depiction of the shape of the triangle, any side can be the base. To understand this, imagine rotating a triangle so that the known side is at the base.
- For example, if you know the area of a triangle is 20, and the length of one side is 4, write: L = 20 and a = 4.

Step 3. Plug the known values into the formula L=1/2at and calculate
First, multiply the base (a) by 1/2, then divide the area (L) by the result. The value obtained is the height of your triangle!
- In the example here: 20 = 1/2(4)t
- 20 = 2t
- 10 = t
Method 2 of 3: Finding the Height of an Equilateral Triangle
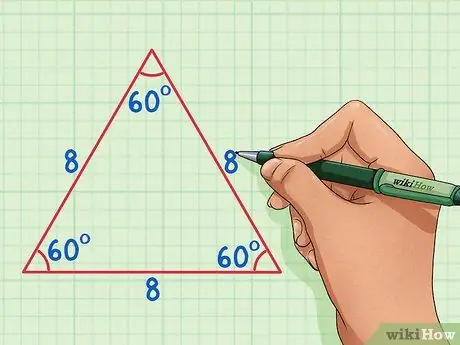
Step 1. Recall the properties of an equilateral triangle
An equilateral triangle has 3 equal sides and three equal angles, each 60 degrees. If an equilateral triangle is divided into two equal parts, you will get two congruent right triangles.
In the example here, we will use an equilateral triangle with each side length of 8
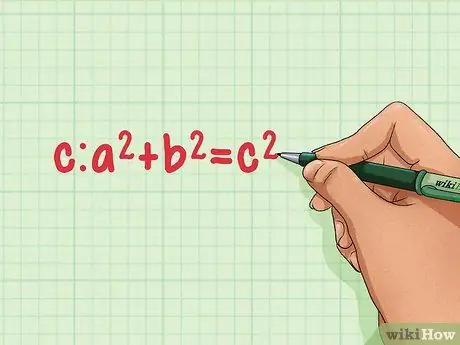
Step 2. Recall the Pythagorean Theorem
The Pythagorean theorem states that for all right triangles with side length a and b, as well as the hypotenuse c apply: a2 + b2 = c2. We can use this theorem to find the height of an equilateral triangle!
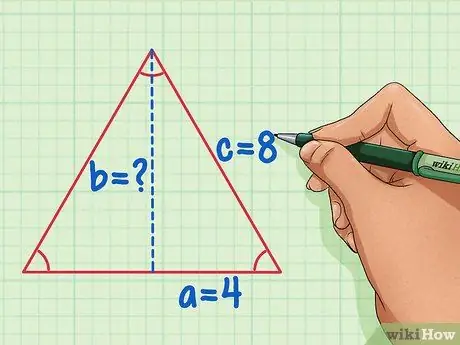
Step 3. Divide the equilateral triangle into two equal parts, and mark the sides as variables a, b, and c.
Length of hypotenuse c will be equal to the length of the side of an equilateral triangle. Side a will be equal to 1/2 the length of the previous side, and side b is the height of the triangle to find.
Using the example of an equilateral triangle with side length = 8 c = 8 and a = 4.
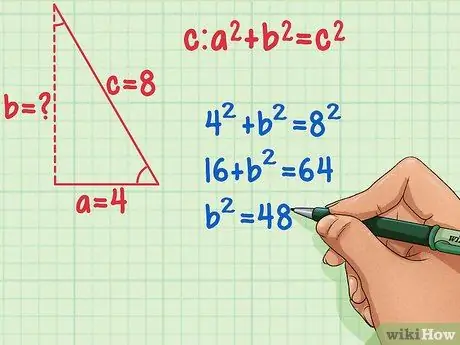
Step 4. Plug this value into the Pythagorean Theorem and find the value of b2.
First square c and a by multiplying each number by the same number. Then, subtract a2 from c2.
- 42 + b2 = 82
- 16 + b2 = 64
- b2 = 48

Step 5. Find the square root of b2 to find out the height of your triangle!
Use the square root function in your calculator to find Sqrt(2). The result of the calculation is the height of your equilateral triangle!
b = Sqrt(48) = 6, 93
Method 3 of 3: Finding Height with Angles and Side Length
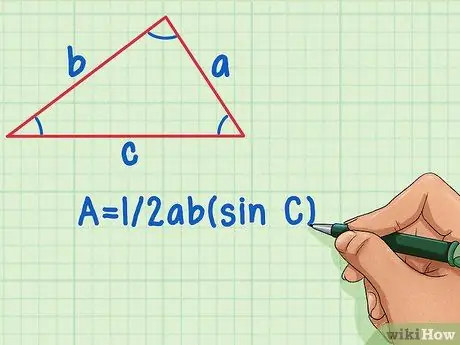
Step 1. Determine the known variables
You can find the height of a triangle if you know the angles and side lengths, if the angle lies between the base and a known side, or all sides of the triangle. We call the sides of the triangle a, b, and c, while the angles are called A, B, and C.
- If you know the lengths of the three sides, you can use Heron's formula, and the formula for the area of a triangle.
- If you know the lengths of two sides of a triangle and an angle, you can use the formula for the area of a triangle based on that data. L = 1/2ab(sin C).

Step 2. Use Heron's formula if you know the lengths of the three angles of the triangle
Heron's formula consists of two parts. First, you have to find the variable s, which is equal to half the perimeter of the triangle. You can calculate it using the formula: s = (a+b+c)/2.
- So for a triangle with sides a = 4, b = 3, and c = 5, s = (4+3+5)/2. So s = (12)/2, s = 6.
- Then, you can continue the calculation using the second part of Heron's formula, Area = sqr(s(s-a)(s-b)(s-c)). Replace the area value in the formula with its equivalent in the triangle area formula: 1/2bt (or 1/2at or 1/2ct).
- Perform calculations to find the value of t. In the example here, the calculation is 1/2(3)t = sqr(6(6-4)(6-3)(6-5)). So 3/2t = sqr(6(2)(3)(1)), which results in 3/2t = sqr(36). Use a calculator to calculate the square root, so you get 3/2t = 6. Thus, the height of the triangle here is 4, with b as the base.

Step 3. Use the formula for the area of a triangle with two sides and one angle, if you know one side and one angle of the triangle
Replace the area of the triangle with the equivalent formula: 1/2at. That way, you'll get a formula like the following: 1/2bt = 1/2ab(sin C). This formula can be simplified to t = a(sin C), by removing the opposite side of the variable.






