- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
Finding the perimeter of a triangle means finding the distance around the triangle. The simplest way to find the perimeter of a triangle is to add up all the side lengths, but if you don't know all the side lengths, you'll need to calculate them first. This article will first teach you to find the perimeter of a triangle when you know all the side lengths; This method is the easiest and most widely used method. Then, this article will explain how to find the perimeter of a right triangle when you only know two sides. Finally, this article will explain how to find the perimeter of any triangle for which you know the two side lengths and the measure of the angle between them using the Law of Cosine.
Step
Method 1 of 3: Finding the Perimeter of a Triangle When You Know All Three Sides

Step 1. Recall the formula for finding the perimeter
The formula is: K= a + b + c. a, b, and c are the lengths of the sides of the triangle and K is the perimeter of the triangle.
The meaning of this formula is simply that to find the perimeter of a triangle, you only need to add up the lengths of all three sides
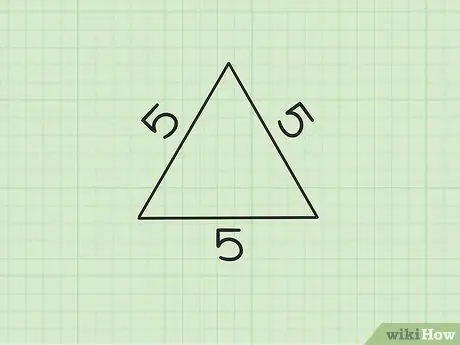
Step 2. Look at your triangle and determine the lengths of its three sides
In this example, the side length a =
Step 5., side length b
Step 5., and side length c
Step 5
This particular example is called an equilateral triangle, because all of its sides are the same length. However, keep in mind that the formula for the perimeter of a triangle is the same for any triangle

Step 3. Add up the lengths of the three sides to find the perimeter of the triangle
In this example, 5 + 5 + 5 = 15. Therefore, K = 15.
-
In another example, where a = 4, b = 3, and c=5, the perimeter of the triangle is: K = 3 + 4 + 5, or
Step 12..
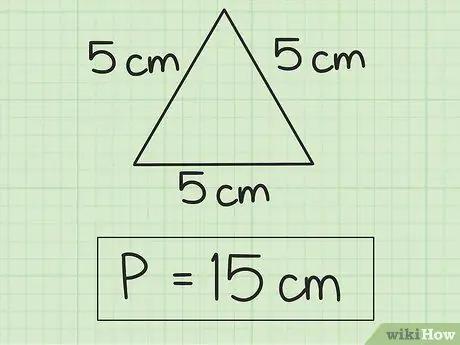
Step 4. Always add units to the final answer
In this example, the sides are measured in centimeters, so the final answer must be in centimeters. The final answer is: K = 15 cm.
Method 2 of 3: Finding the Perimeter of a Triangle from a Right-angled Triangle That Knows Two Sides
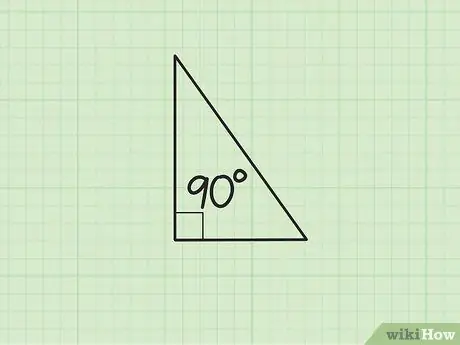
Step 1. Remember what a right triangle is
A right triangle is a triangle that has one right angle (90 degrees). The side of the triangle opposite the right angle is the longest side, and is called the hypotenuse. Right triangles show up frequently on math exams, and luckily there's a very easy formula for finding the length of an unknown side.
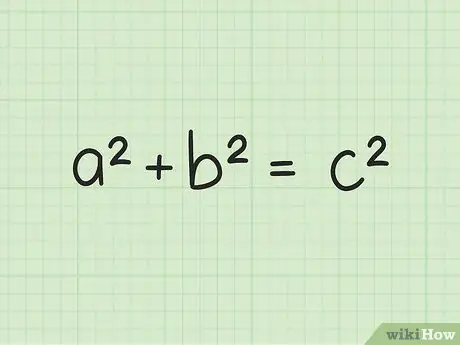
Step 2. Recall the Pythagorean Theorem
The Pythagorean theorem states that for any right triangle with side lengths a and b, and the hypotenuse c holds, a2 + b2 = c2.
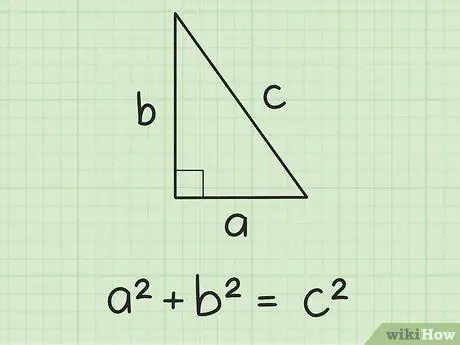
Step 3. Look at your triangle, and mark the sides with "a," "b," and "c"
Remember that the longest side of a triangle is called the hypotenuse. This side will be opposite to the right angle and must be marked as c. Mark the two shorter sides as a and b. It doesn't matter which side you will mark as a and b, the calculation result will be the same!
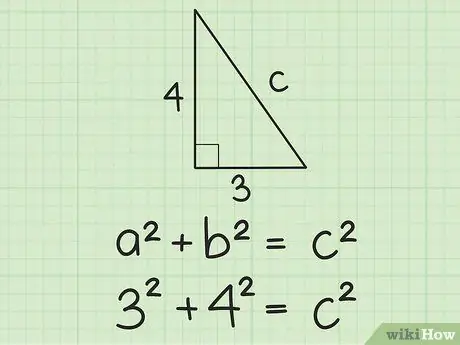
Step 4. Plug the known side lengths into the Pythagorean Theorem
Remember that a2 + b2 = c2. Change the side length according to the letter variable in the formula.
- If, for example, you know that the side length a = 3 and side b = 4, then, plug that value into the formula as follows: 32 + 42 = c2.
- If you know that the side length a = 6, and the hypotenuse c = 10, then you have to enter it into the formula as follows: 62 + b2 = 102.

Step 5. Solve the above equation to find the length of the unknown side
First of all, you need to know the square of the known side lengths. This means you have to multiply the side length by its own value (for example 32 = 3 * 3 = 9). If you're looking for the length of the hypotenuse, simply add up the squares of the two sides of the triangle and find the square root of the result. If the unknown is the other side, then you have to do a simple subtraction, and then take the square root of the result to get the side you're looking for.
- In the first example, add up the squares of 32 + 42 = c2 and obtained 25= c2. Then calculate the square root of 25 to find the side length c = 5.
- In the second example, square the side lengths in the equation 62 + b2 = 102 and obtained 36 + b2 = 100. Subtract 36 from the square of the hypotenuse, to get b2 = 64, then, take the square root of 64 to get b = 8.
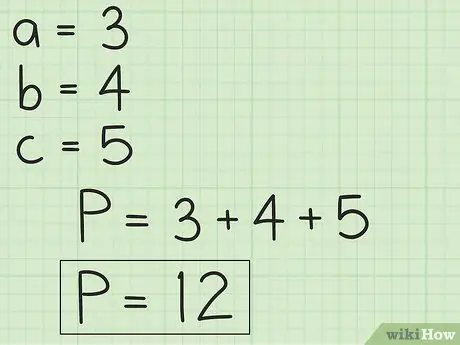
Step 6. Add up all the side lengths of the triangle to find the perimeter
Remember that the perimeter of the triangle K = a + b + c. Now that you know all the side lengths of the triangle a, b and c, you just need to add all three to find the perimeter.
- In our first example, K = 3 + 4 + 5, or 12.
- In our second example, K = 6 + 8 + 10, or 24.
Method 3 of 3: Finding the Perimeter of an Irregular Triangle Using the Law of Cosine
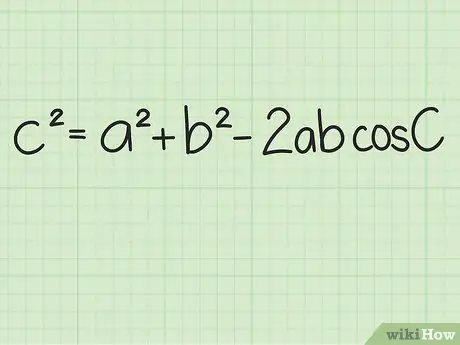
Step 1. Study the Law of Cosines
The law of cosines allows you to solve any triangle problem when you only know the two side lengths and the measure of the angle between the two sides. This law can be used for all triangles, and is a very useful formula. The law of cosines states that for any triangle with side a, b, and c, with opposite angle A, B, and C: c2 = a2 + b2 - 2ab cos(C).

Step 2. Take a look at your triangle and place the variable letters into the triangle section
The first side you know should be marked as a, and the angle opposite the side as A. The second side that you know should be marked as b; and the angle opposite the side as B. The angle you know should be marked as C, and the third side, the side you need to calculate to find the perimeter of the triangle, as c.
-
For example, imagine a triangle with sides 10 and 12, and the angle between them is 97°. We will enter the variables as follows: a = 10, b = 12, C = 97°.

Step 3. Plug the values you know into the formula and solve to get the value of c
First you need to find the square of a and b, and add them together. Then, find the cosine value of C using the "cos" function on your calculator, or an online cosine calculator. Multiply value cos(C) with value 2ab and subtract the result from the sum of a2 + b2. the result is value c2. Find the square root of this value and you will get the side length c. Using our triangle example:
- c2 = 102 + 122 - 2×10×12×cos(97).
- c2 = 100 + 144 - (240 × -0, 12187) (Round the cosine value to a number with 5 decimal places.)
- c2 = 244 - (-29, 25)
- c2 = 244 + 29, 25 (Keep carrying the minus symbol if the result of cos(C) is negative!)
- c2 = 273, 25
- c = 16, 53
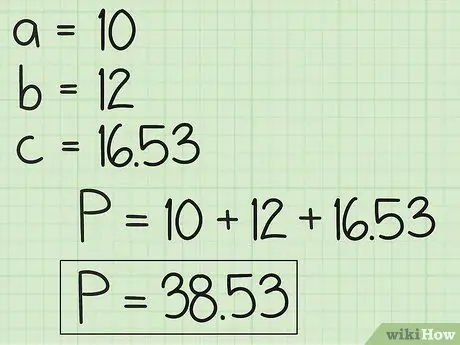
Step 4. Use side c to find the perimeter of the triangle
Recall that the perimeter of a triangle is K = a + b + c, so all you need to do is add up the length you just got, which is the side c with a known side length, i.e a and b. So easy!






