- Author Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
The P value is a statistical measurement that helps scientists determine if their hypothesis is correct. The P value is used to determine if the results of their experiment are within the range of values that are normal for the things being studied. Usually, if the P value of a data set falls below a certain predetermined value (for example, 0.05), scientists will reject the null hypothesis of their experiment - in other words, they will rule out a hypothesis where the experimental variable has no significant effect. on the result. Nowadays, p values are usually found in reference tables by calculating the chi squared value.
Step

Step 1. Determine the expected results of your experiment
Usually, when scientists conduct an experiment and examine the results, they already have an idea of the normal or ordinary results beforehand. This can be based on the results of previous experiments, reliable observational data sets, scientific literature, and/or other sources. For your experiment, determine your expected result and write it down as a number.
Example: Suppose a previous study showed that, at the national level, speeding tickets were issued more often to red cars than to blue cars. Suppose the average result at the national level shows a ratio of 2:1 with the ratio of red cars being more. We want to find out if the police in our city also get the same tendency by analyzing the speeding ticket issued by the police in our city. If we took a random sample of 150 speeding tickets given to both red and blue cars in our city, we would expect 100 for red car and 50 for blue cars if the police unit in our city gives a ticket according to the comparison at the national level.

Step 2. Determine your experimental observations
Now that you've determined your expected value, you can run your experiment and find the true value (or observation). Again, write down the result as a number. If we manipulate some experimental conditions and the observed results differ from the expected results, two possibilities exist: either this happened by chance, or it was our manipulation of the experimental variables that caused this difference. The purpose of finding the p-value is basically to determine if the observed results differ from the expected results to a point where the null hypothesis - the hypothesis that there is no relationship between the experimental variable and the observed results - cannot be rejected.
Example: Suppose, in our city, we randomly select 150 speeding tickets that are awarded to both red and blue cars. We get 90 a ticket for a red car and 60 for the blue car. This is different from the result we expected which is 100 and 50. Did our experimental manipulation (in this case, changing the data source from national to local) cause any change in the results, or did our city police have the same tendencies as the national level, and we just observed coincidence? The p value will help us determine it.

Step 3. Determine the degrees of freedom for your experiment
The degrees of freedom are a measure of the amount of variability in the study, which is determined by the number of categories you examine. The equation for the degrees of freedom is Degrees of freedom = n-1, where n is the number of categories or variables analyzed in your experiment.
-
Example: Our experiment has two categories of results: one for the red car and one for the blue car. Thus, in our experiment, we have 2-1 = 1 degree of freedom.
If we compare red, blue, and green cars, we will have
Step 2. degrees of freedom and so on.

Step 4. Compare the expected results with the observed results using chi squared
Chi squared (written x2) is a numerical value that measures the difference between the expected and observed values from the experiment. The equation for chi squared is: x2 = ((o-e)2/e), where o is the observed value and e is the expected value. Add up the results of this equation for all possible outcomes (see below).
- Note that this equation uses the (sigma) operator. In other words, you have to calculate ((|o-e|-.05)2/e) for each possible outcome, then add up the results to get the chi squared value. In our example, we have two results - a car that gets a red or a blue ticket. Thus, we can calculate ((o-e)2/e) twice - once for the red car and once for the blue car.
-
Example: Let's plug our expected values and observations into the equation x2 = ((o-e)2/e). Remember that, because of the sigma operator, we have to compute ((o-e)2/e) twice - once for the red car and once for the blue car. The processing steps are as follows:
- x2 = ((90-100)2/100) + (60-50)2/50)
- x2 = ((-10)2/100) + (10)2/50)
- x2 = (100/100) + (100/50) = 1 + 2 = 3.

Step 5. Choose a level of significance
Now that we know our experimental kit's degrees of freedom and the chi squared value, there's only one last thing we need to do before we can find our p-value - we need to determine the level of significance. Basically, significance level is a measurement of how sure we are of our results - a low level of significance corresponds to a low probability that the outcome of an experiment was due to chance and vice versa. The level of significance is written as a decimal (eg 0.01), which corresponds to the percent chance that the outcome of the experiment was due to chance (in this case, 1%).
- By convention, scientists usually set a significance value for their experiments at 0.05 or 5 percent. This means that experimental results that correspond to this level of significance have, at most, a 5% chance of coincidence. In other words, there is a 95% chance that the results are due to the scientist's manipulation of the experimental variables, and not chance. For most experiments, 95% confidence about the relationship between the two variables, is considered to have been successful in demonstrating the relationship between the two.
- Example: For our red and blue car example, let's follow the scientific agreement and determine our significance level of 0, 05.
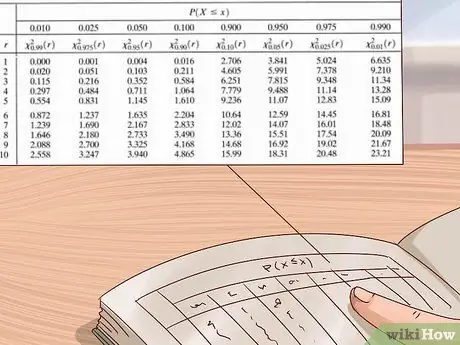
Step 6. Use the chi square distribution table to estimate your p-value
Scientists and statisticians use large tables of values to calculate p values for their experiments. This table is usually written with the vertical axis on the left showing the degrees of freedom and the horizontal axis on the top showing the p-values. Use this table by first finding your degrees of freedom, then reading the rows from left to right until you find the first value that is greater than your chi squared value. Look at the p-value at the top of the column - your p-value is between this value and the next largest value (the right value is to the left of it).
- Chi square distribution tables are available from a variety of sources - they can easily be found online or in science or statistics textbooks. If you don't have one, use the table shown in the photo above or a free online table, such as the one provided by medcalc.org here.
-
Example: Our chi squared is 3. So let's use the chi square distribution table in the photo above to find an approximate p-value. Since we know that our experiment only has
Step 1. degrees of freedom, we'll start from the top table. We go from left to right in this row until we find a value higher than
Step 3. - our chi squared value. The first value we find is 3.84. Looking up this column, we see that the corresponding p-value is 0.05. This means that our p-value is between 0.05 and 0.1 (next largest p-value in the table).

Step 7. Decide whether to reject or defend your null hypothesis
Since you have found an approximate p-value for your experiment, you can decide whether or not to reject your experiment's null hypothesis (as a reminder, this is the hypothesis that the experimental variable you manipulated had no effect on the results you observed). If your p-value is lower than your significance value, congratulations - you have proven that there is a high probability that there is a relationship between the variables you manipulated and your observations. If your p-value is greater than your significance value, you cannot say with certainty that the results you are observing are the result of mere coincidence or manipulation of your experiment.
- Example: Our p-value is between 0.05 and 0.1. That is, it is by no means less than 0.05, so, unfortunately, we cannot reject our null hypothesis. This means that we do not reach the minimum 95% confidence limit that we have set so that it can be said that the police in our city give ticketing tickets to red and blue cars in a ratio that is quite different from the national average.
- In other words, there is a 5-10% chance that our observations are not the result of a change in location (analyzing our city, and not the whole part), but are coincidences. Since we are looking for a probability of less than 5%, we can't say that we convinced that the police in our city tend to ticket red cars - there is a slight but statistically very different possibility that they do not have this tendency.
Tips
- A scientific calculator will make the calculations much easier. You can also search for calculators online.
- You can calculate p-values using several computer programs, including commonly used spreadsheet software and more specialized statistical software.






