5 Ways to Find the Value of X

2024 Author: Jason Gerald | [email protected]. Last modified: 2024-01-15 08:07

There are several ways to find the value of x, whether you're working with squares and roots or if you're just dividing or multiplying. No matter which process you use, you can always find a way to move x to one side of the equation so you can find its value. Here's how to do it:

Step

Method 1 of 5: Using Basic Linear Equations

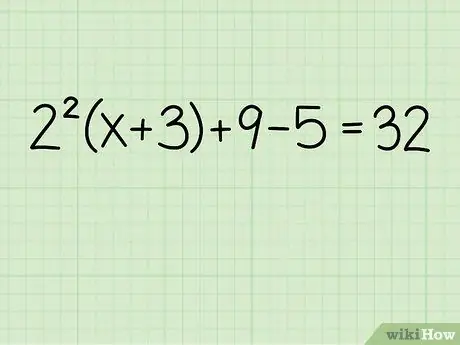
Step 1. Write down the problem, like this:

2²(x+3) + 9 - 5 = 32

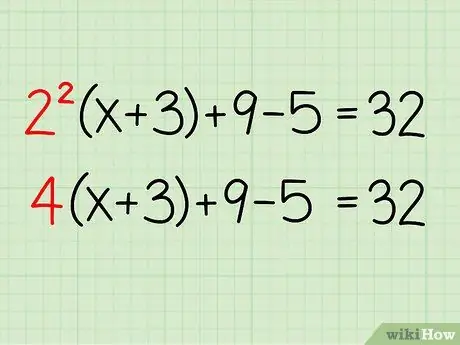
Step 2. Solve the square

Remember the order of number operations starting from parentheses, squares, multiplication/division, and add/subtract. You can't finish the brackets first because x is in brackets, so you have to start with the square, 2². 2² = 4

4(x+3) + 9 - 5 = 32

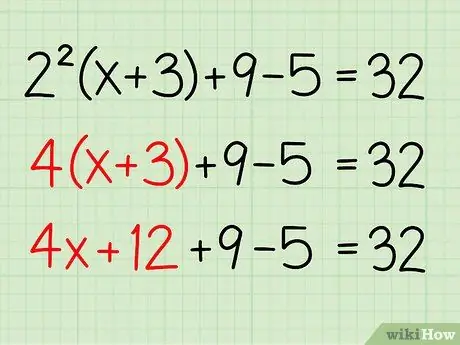
Step 3. Multiply

Multiply the number 4 by (x + 3). Here's how:

4x + 12 + 9 - 5 = 32

Step 4. Add and subtract

Just add or subtract the remaining numbers, like this:

• 4x+21-5 = 32
• 4x+16 = 32
• 4x + 16 - 16 = 32 - 16
• 4x = 16

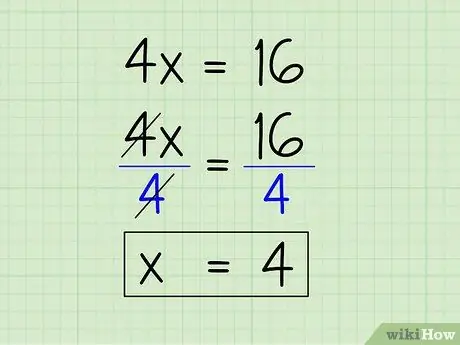
Step 5. Find the value of the variable

To do this, divide both sides of the equation by 4 to find x. 4x/4 = x and 16/4 = 4, so x = 4.

• 4x/4 = 16/4
• x = 4

Step 6. Check your calculations

Plug x = 4 into the original equation to make sure the result is correct, like this:

• 2²(x+3)+ 9 - 5 = 32
• 2²(4+3)+ 9 - 5 = 32
• 2²(7) + 9 - 5 = 32
• 4(7) + 9 - 5 = 32
• 28 + 9 - 5 = 32
• 37 - 5 = 32
• 32 = 32

Method 2 of 5: By Square

Step 1. Write down the problem

For example, suppose you are trying to solve a problem with the variable x squared:

2x² + 12 = 44

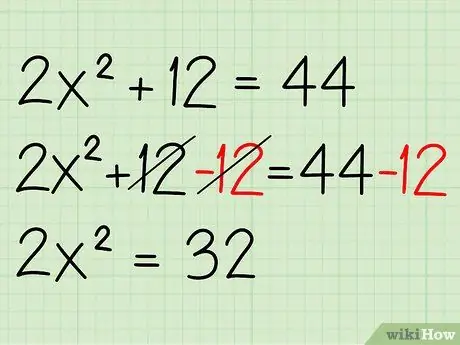
Step 2. Separate the squared variables

The first thing you have to do is combine the variables so that all the equal variables are on the right side of the equation while the squared variables are on the left. Subtract both sides by 12, like this:

• 2x²+12-12 = 44-12
• 2x² = 32

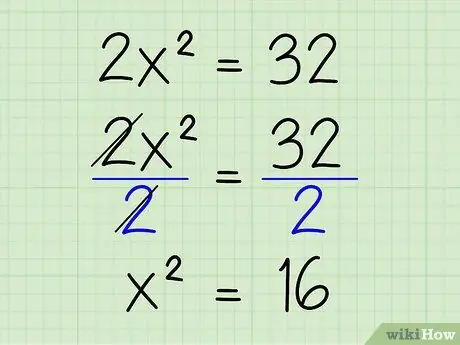
Step 3. Separate the squared variables by dividing both sides by the coefficient of the variable x

In this case 2 is the coefficient of x, so divide both sides of the equation by 2 to eliminate it, like this:

• (2x²)/2 = 32/2
• x² = 16

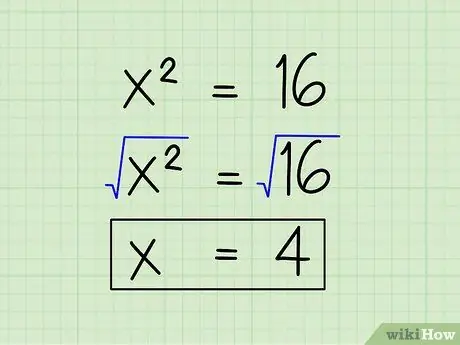
Step 4. Find the square root of both sides of the equation

Don't just find the square root of x², but find the square root of both sides. You'll get the x on the left and the square root of 16, which is 4 on the right. So, x = 4.

Step 5. Check your calculations

Plug x = 4 back into your original equation to make sure the result is correct. Here's how:

• 2x² + 12 = 44
• 2 x (4)² + 12 = 44
• 2 x 16 + 12 = 44
• 32 + 12 = 44
• 44 = 44

Method 3 of 5: Using Fractions

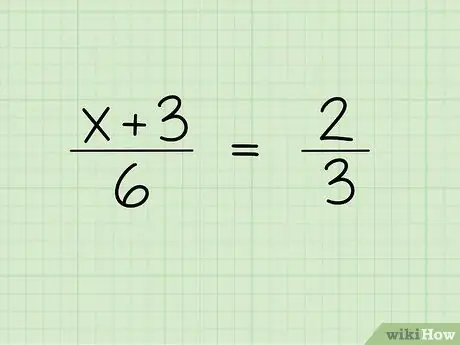
Step 1. Write down the problem

For example, you want to solve the following questions:

(x + 3)/6 = 2/3

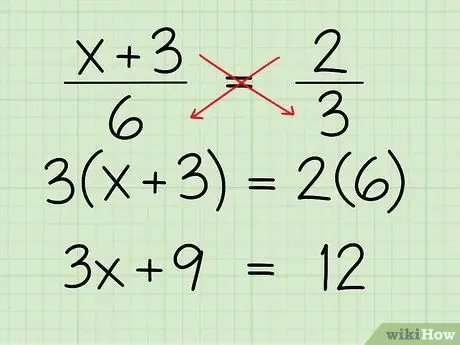
Step 2. Cross multiply

To cross multiply, multiply the denominator of each fraction by the numerator of the other fraction. In short, you multiply it diagonally. So, multiply the first denominator, 6, by the second, 2, so you get 12 on the right side of the equation. Multiply the second denominator, 3, by the first, x + 3, so you get 3 x + 9 on the left side of the equation. Here's how:

• (x + 3)/6 = 2/3
• 6 x 2 = 12
• (x + 3) x 3 = 3x + 9
• 3x + 9 = 12

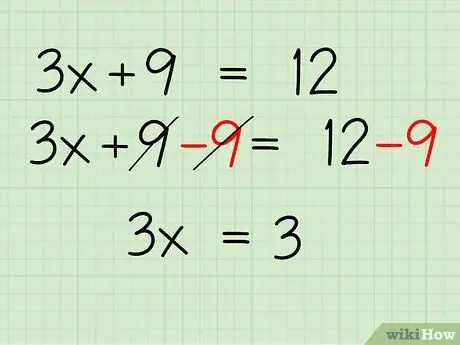
Step 3. Combine the same variables

Combine the constants in the equation by subtracting both sides of the equation by 9, like this:

• 3x + 9 - 9 = 12 - 9
• 3x = 3

Step 4. Separate x by dividing each side by the coefficient of x

Divide 3x and 9 by 3, the coefficient of x, to get the value of x. 3x/3 = x and 3/3 = 1, so x = 1.

Step 5. Check your calculations

To check, plug x back into the original equation to make sure that the result is correct, like this:

• (x + 3)/6 = 2/3
• (1 + 3)/6 = 2/3
• 4/6 = 2/3
• 2/3 = 2/3

Method 4 of 5: Using Square Roots

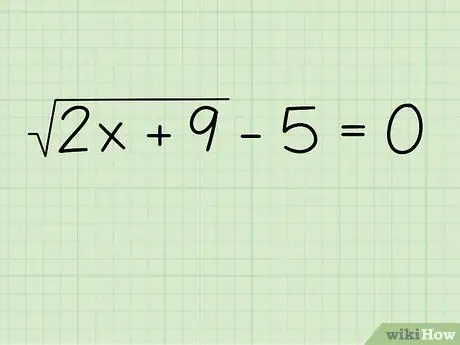
Step 1. Write down the problem

For example, you would find the value of x in the following equation:

(2x+9) - 5 = 0

Step 2. Split the square root

You must move the square root to the other side of the equation before you can continue. So, you have to add up both sides of the equation by 5, like this:

• (2x+9) - 5 + 5 = 0 + 5
• (2x+9) = 5

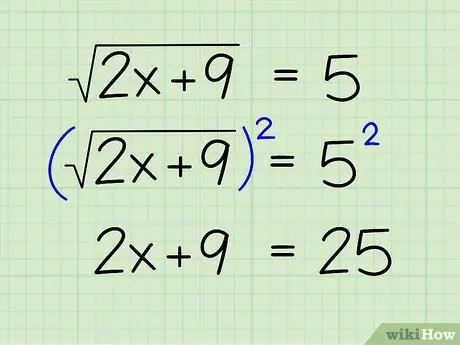
Step 3. Square both sides

Just as you divide both sides of the equation by the coefficient x, you must square both sides if x appears in the square root. This will remove the sign (√) from the equation. Here's how:

• (√(2x+9))² = 5²
• 2x + 9 = 25

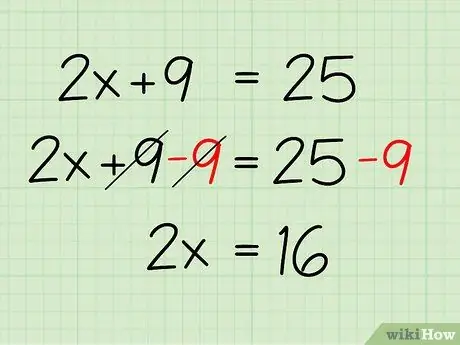
Step 4. Combine the same variables

Combine the same variables by subtracting both sides by 9 so that all the constants are on the right side of the equation and x is on the left, like this:

• 2x + 9 - 9 = 25 - 9
• 2x = 16

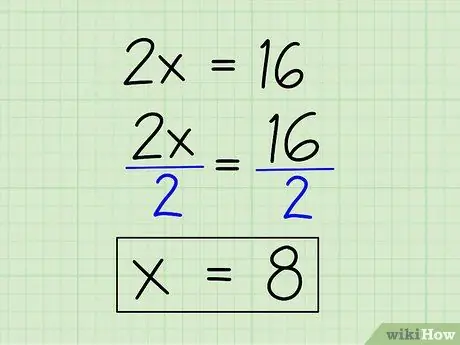
Step 5. Separate the variables

The last thing you have to do to find the value of x is to separate the variable by dividing both sides of the equation by 2, the coefficient of the variable x. 2x/2 = x and 16/2 = 8, so x = 8.

Step 6. Check your calculations

Re-enter the number 8 in the equation to see if your answer is correct:

• (2x+9) - 5 = 0
• √(2(8)+9) - 5 = 0
• √(16+9) - 5 = 0
• √(25) - 5 = 0
• 5 - 5 = 0

Method 5 of 5: Using Absolute Signs

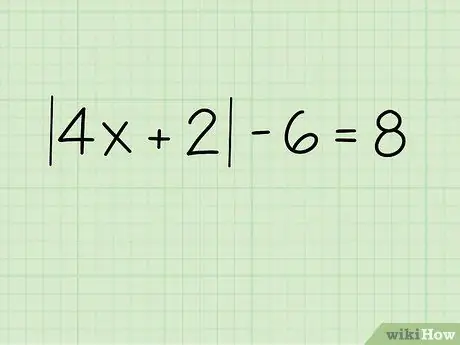
Step 1. Write down the problem

For example, suppose you are trying to find the value of x from the following equation:

|4x +2| - 6 = 8

Step 2. Separate the absolute sign

The first thing you have to do is combine the same variables and move the variable in absolute sign to the other side. In this case, you have to add both sides by 6, like this:

• |4x +2| - 6 = 8
• |4x +2| - 6 + 6 = 8 + 6
• |4x +2| = 14

Step 3. Remove the absolute sign and solve the equation This is the first and easiest way

You must find the value of x twice when calculating the absolute value. Here's the first method:

• 4x + 2 = 14
• 4x + 2 - 2 = 14 -2
• 4x = 12
• x = 3

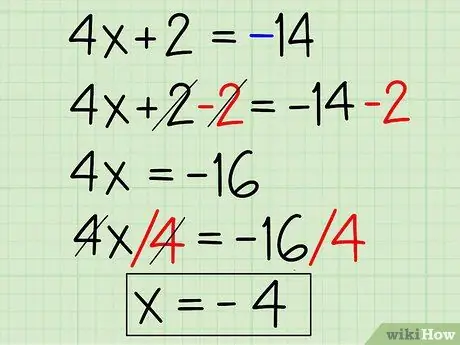
Step 4. Remove the absolute sign and change the sign of the variable on the other side before finishing

Now, do it again, except let the sides of the equation be -14 instead of 14, like this:

• 4x + 2 = -14
• 4x + 2 - 2 = -14 - 2
• 4x = -16
• 4x/4 = -16/4
• x = -4

Step 5. Check your calculations

If you already know that x = (3, -4), plug the two numbers back into the equation to see if the result is correct, like this:

• (For x = 3):

  • |4x +2| - 6 = 8
  • |4(3) +2| - 6 = 8
  • |12 +2| - 6 = 8
  • |14| - 6 = 8
  • 14 - 6 = 8
  • 8 = 8

• (For x = -4):

  • |4x +2| - 6 = 8
  • |4(-4) +2| - 6 = 8
  • |-16 +2| - 6 = 8
  • |-14| - 6 = 8
  • 14 - 6 = 8
  • 8 = 8

Tips

• The square root is another way of describing the square. The square root of x = x^1/2.
• To check your calculations, plug the value of x back into the original equation and solve.