- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
Squaring fractions is one of the simplest operations on fractions. The method is similar to squaring all numbers in that you simply multiply the numerator and divisor by the number itself. There are also cases where simplifying a fraction makes squaring easier. If you don't know it already, this article will provide an easy review that will make your understanding easier.
Step
Part 1 of 3: Squaring Fractions
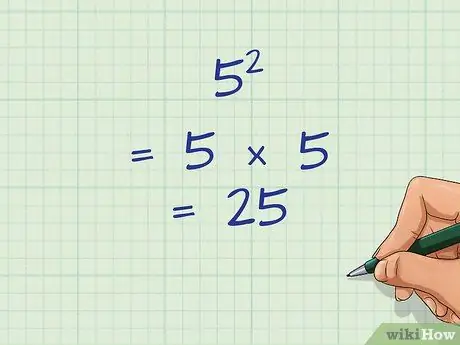
Step 1. Understand how to square all numbers
When you see a power of two, it means that the number needs to be squared. To do this, multiply the number by the number itself. As an example:
52 = 5 × 5 = 25
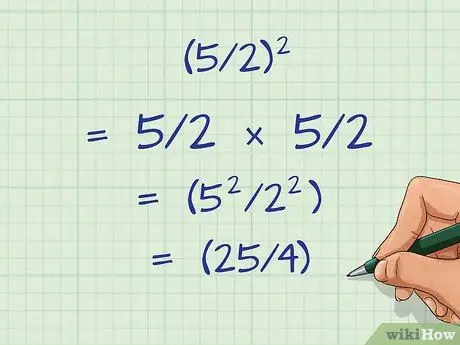
Step 2. Know that squaring fractions works the same way
To square a fraction, you multiply the fraction by the fraction itself. You can do this by multiplying the numerator and divisor by the number itself. As an example:
- (5/2)2 = 5/2 × 5/2 or (52/22).
- Squaring each number yields (25/4).
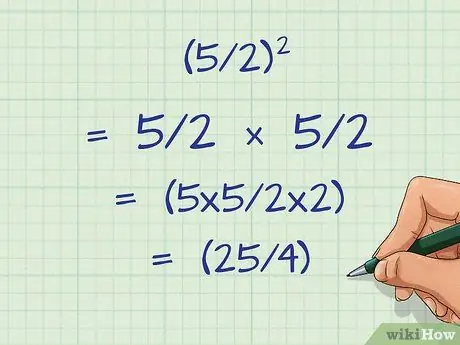
Step 3. Multiply the numerator by itself, and the divisor by itself
The order doesn't matter as long as you square the two numbers. To simplify things, start with the numerator: multiply the number by the number itself. Then, multiply the divisor by the number itself.
- In fractions, the numerator is the number on top and the divisor is the number on the bottom.
- As an example: (5/2)2 = (5 x 5/2 x 2) = (25/4).
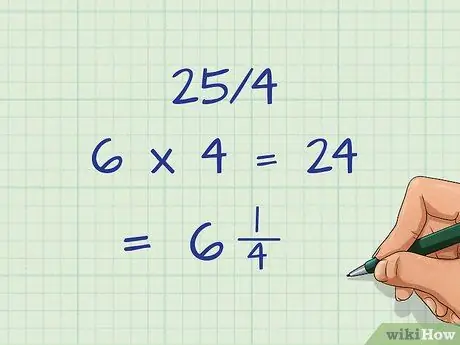
Step 4. Simplify the fraction
When working with fractions, the final step is always to reduce the fraction to its simplest form, or to convert an inappropriate fraction to a mixed number. From our example, 25/4 is an incorrect fraction because the numerator is greater than the divisor.
To convert a fraction to a mixed number, for example 25 divided by 4. Multiply it 6 times (6 x 4 = 24) with a remainder of 1. Therefore, the mixed number is 6 1/4.
Part 2 of 3: Squaring Fractions with Negative Numbers
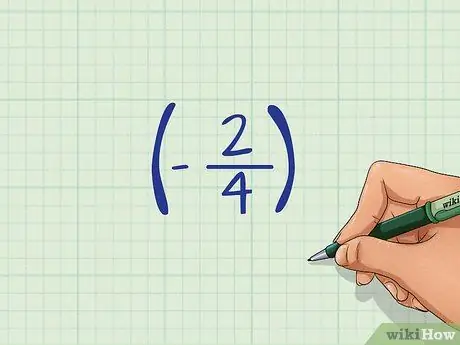
Step 1. Know the negative sign in front of the fraction
If you're working with a negative fraction, a minus sign will be in front of it. It's a good practice to put negative numbers in parentheses so you know the "-" sign refers to a number and not to subtract two numbers.
As an example: (-2/4)

Step 2. Multiply the fraction by the number itself
Square fractions as normal by multiplying the numerator and divisor by their own number. Alternatively, you can multiply the fraction by the number of the fraction itself.
As an example: (-2/4)2 = (-2/4) x (-2/4)
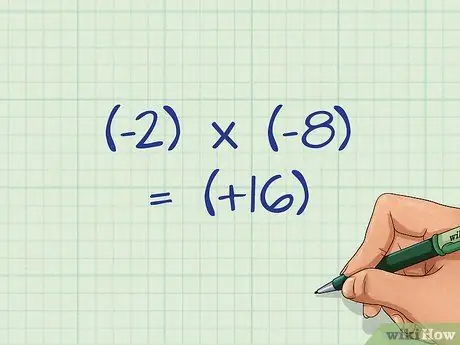
Step 3. Understand that multiplying two negative numbers results in a positive number
When there is a minus sign, all fractions are negative. When you square a fraction, you multiply two negative numbers, the result is a positive number.
For example: (-2) x (-8) = (+16)
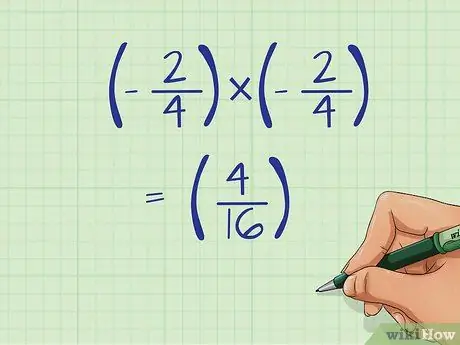
Step 4. Remove the negative sign after the number is squared
By squaring a fraction, you are multiplying two negative numbers. That is, squaring the fraction will result in a positive number. Make sure you write down the answer without the negative sign.
- Continuing the example above, the result of squaring the fraction is a positive number.
- (-2/4) x (-2/4) = (+4/16)
- Usually, you don't need to write a "+" sign to indicate a positive number.
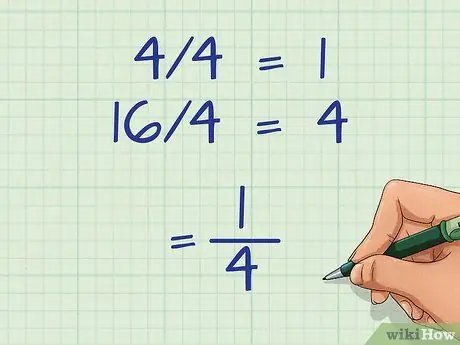
Step 5. Reduce the fraction to its simplest form
The final step in all calculations involving fractions is always simplification. Fractions that do not match must be simplified to mixed numbers and then reduced.
- As an example: (4/16) has a common factor of 4.
- Divide the fraction by 4: 4/4 = 1, 16/4= 4
- Convert to simple fraction:(1/4)
Part 3 of 3: Using Simplifications and Shortcuts
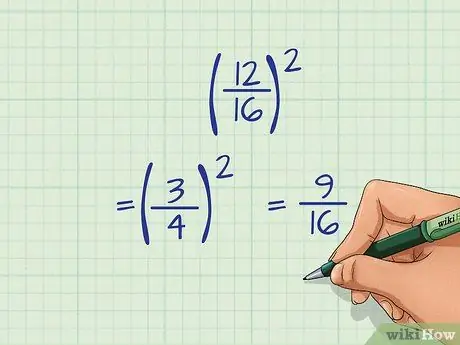
Step 1. Check if you can Simplify the Fraction before squaring
Usually, fractions are easier to square if they were previously simplified. Remember, subtracting a fraction means dividing by its common factor until only one can divide both the numerator and the divisor. Subtracting the fraction first means that there is no need for simplification at the end of the calculation.
- As an example: (12/16)2
- 12 and 16 are divisible by 4. 12/4 = 3 and 16/4 = 4. Therefore, 12/16 reduced to 3/4.
- Now, you will square the fraction 3/4.
- (3/4)2 = 9/16, which cannot be simplified any further.
-
To prove it, let's square the fraction without simplification:
- (12/16)2 = (12 x 12/16 x 16) = (144/256)
- (144/256) has a common factor of 16. Dividing the numerator and divisor by 16 reduces the fraction to (9/16). We can see, the simplification at the beginning and the end produces the same fraction.

Step 2. Learn to know when to defer fraction simplification
When solving more complex equations, you can delay one of the factors. In this case, it's actually easier to do the calculations if you delay the fraction simplification. We will factor in additional from the above example.
- For example: 16 × (12/16)2
- Break down the square and cross out the common factor of 16: 16 * 12/16 * 12/16
Since there is one 16 in the integer and two 16 in the divisor, you can cross ONE of them
- Rewrite the simplified equation: 12 × 12/16
- Subtract 12/16 by dividing by 4: 3/4
- Multiply: 12 × 3/4 = 36/4
- Divide: 36/4 = 9
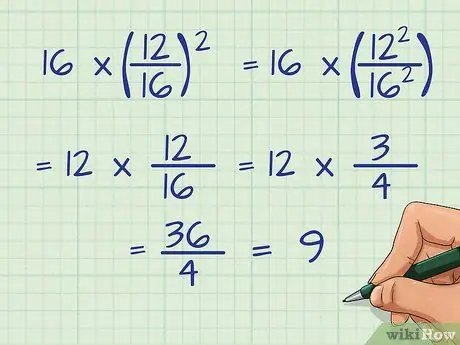
Step 3. Understand how to use exponential shortcuts
Another way to solve the same example is to simplify the exponent. The end result is the same, only the solution is different.
- For example: 16 * (12/16)2
- Rewrite with squared numerator and divisor: 16 * (122/162)
- Remove the exponent in the divisor: 16 * 122/162
Imagine the first 16 has an exponent of 1:161. Using the rules for dividing exponential numbers, subtract the exponents. 161/162, the result is 161-2 = 16-1 or 1/16.
- Now, you do: 122/16
- Rewrite and simplify the fraction: 12*12/16 = 12 * 3/4.
- Multiply: 12 × 3/4 = 36/4
- Divide: 36/4 = 9






