- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
Counting fractions is one of the most useful math skills to develop. Before doing fractional calculations, learn how to identify parts and types of fractions. After that, you can add or subtract them. For more complex calculations, learn how to multiply and divide fractions. Usually, you'll also need to simplify or reduce fractions.
Step
Method 1 of 4: Recognizing Fractions

Step 1. Find the fraction
Fractions are written as one number above the dividing line, and another number below the line.

Step 2. Identify the numerator
The number above the line is called the numerator and shows how many parts there are in the fraction.
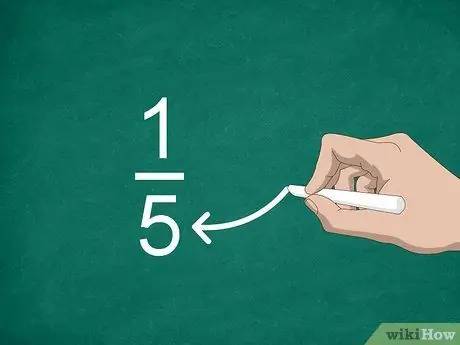
For example, in the fraction 1/5, “1” is the numerator
Step 3. Find the denominator
The number placed below the line is called the denominator. This value indicates the number of parts that "construct" an integer.
For example, in the fraction 1/5, "5" is the denominator so there are five parts to the fraction

Step 4. Determine whether the fractions are reasonable fractions or improper fractions
If the numerator is smaller than the denominator, the fraction is a natural fraction. In improper fractions, the value of the numerator is greater than the value of the denominator.
- For example, 3/4 is a reasonable fraction and 5/3 is an improper fraction.
- If you have an integer that includes a fraction, the number is known as a mixed number. For example, 1 1/2 is a mixed number.
Method 2 of 4: Add or Subtract Fractions

Step 1. Identify fractions with the same denominator
If you need to add or subtract fractions, each fraction must have the same denominator before you perform the calculation. Observe the denominator of each fraction to make sure that they are all equal (similar).
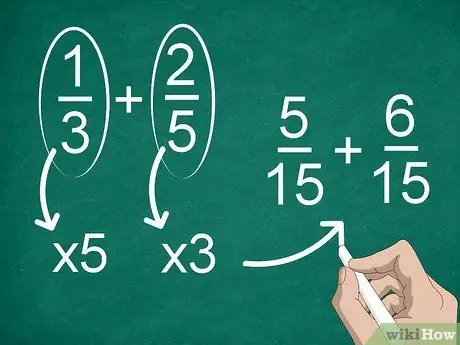
Step 2. Find a common denominator if each fraction has a different denominator
If the denominators are not the same, you will need to change the fractions to have the same denominator. To find a common denominator, multiply each fraction by the denominator of the other.
For example, to find a common denominator in 1/3 + 2/5, multiply “1” and “3” by “5”, then multiply “2” and “5” by “3”. Now, you have the addition of 5/15 + 6/15. After that, you can calculate the fractions
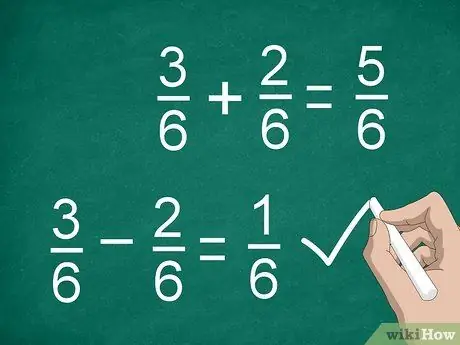
Step 3. Add or subtract the numerators to calculate fractions
Once you've found a common denominator and multiplied the numerators (if necessary), you're ready to add or subtract. Add or subtract the numerators and place the result above the dividing line. Write the common denominator below the line.
- For example, 3/6 - 2/6 = 1/6.
- Don't add or subtract the denominators.
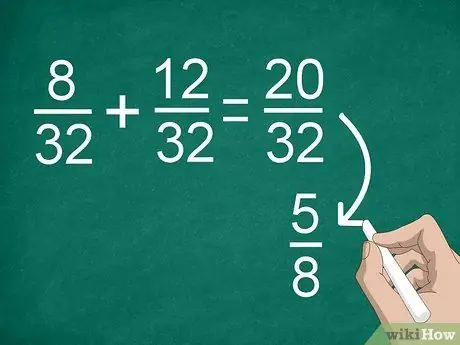
Step 4. Simplify the results if necessary
If you previously needed to find a common denominator, you might get a large fraction that you can simplify. For example, if you add 8/32 +12/32, you will get “20/32” as the result. This fraction can be simplified to “5/8”.
Method 3 of 4: Multiplying and Simplifying Fractions

Step 1. Convert mixed fractions or integers to improper fractions
To make multiplication easier, you need to convert each number to a reasonable or improper fraction. If you have whole numbers or mixed numbers that need to be multiplied, first convert them to a common fraction (natural or improper).
- For example, to multiply 2/5 by 7, convert "7" to a fraction. After that, you can multiply 2/5 by 7/1.
- If you have a mixed number like 1 1/3, convert it to an improper fraction (“4/3”) before multiplying.
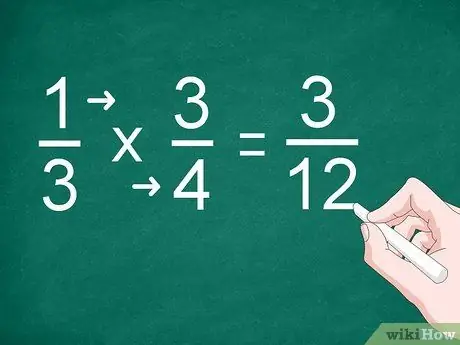
Step 2. Multiply each numerator and denominator
Instead of doing addition, multiply the numerator and write the result above the dividing line. You also need to multiply the denominators and write the result below the line.
For example, to multiply 1/3 by 3/4, multiply “1” by “3” to get the numerator. Multiply “3” by “4” to get the denominator. The answer to the multiplication is "3/12"

Step 3. Simplify the results
Usually, you will need to reduce the result to a simpler form, especially if you initially have unnatural fractions. Find the greatest common factor and use that factor to simplify the numerator and denominator.
For example, for the fraction 3/12, the greatest common factor between “3” and “12” is “3”. Divide each element of the fraction by “3” until you get the fraction “1/4”
Method 4 of 4: Divide Fractions
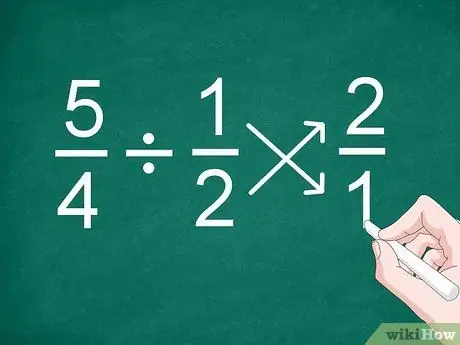
Step 1. Reverse the position of the second fraction
The easiest way to divide fractions, even fractions with different denominators, is to reverse the position of the second fraction before you calculate the result.
For example, for the problem 5/4 1/2, reverse the position of the fraction “1/2” to become “2/1”
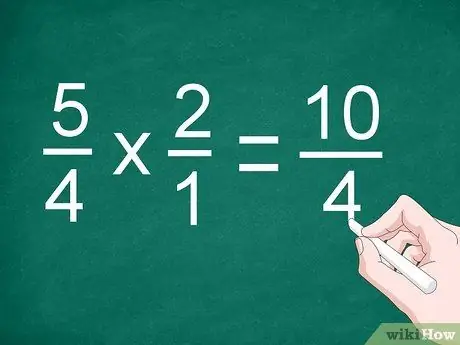
Step 2. Multiply the numerator and denominator
Multiply fractions directly to multiply the numerators. Write the result above the dividing line, then multiply the denominator. Record the product of the denominators below the line.
For the previous example, multiply 5/4 by 2/1 to get “10/4”
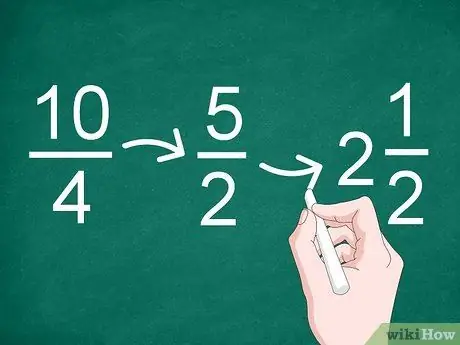
Step 3. Simplify the results if necessary
If the result of the division is an improper fraction or can be reduced, simplify the fraction. Use the greatest common factor to reduce the fraction.
- For example, the greatest common factor in the fraction 10/4 is “2” so the result of the simplification becomes “5/2” (10 divided by 2, and 4 divided by 2).
- Since the result of the simplification is an improper fraction, you can convert it to an integer and a fraction (a mixed number). Therefore, 5/2 can be changed to “2”.
Tips
- If you're working with complex fractions, you'll need to take a few additional steps to simplify the fraction. However, this simplification itself is a mandatory part of the calculation process.
- Always write fractions neatly to reduce the risk of miscalculations.






