- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
For most people, fractions are the first complicated calculations to come across. The concept of fractions is quite difficult and requires you to learn special conditions to do it. Because fractions have special rules for addition, subtraction, multiplication and division, many people are confused about it. However, with a lot of practice, anyone can learn and complete calculations related to fractions.
Step
Method 1 of 5: Understanding Fractions
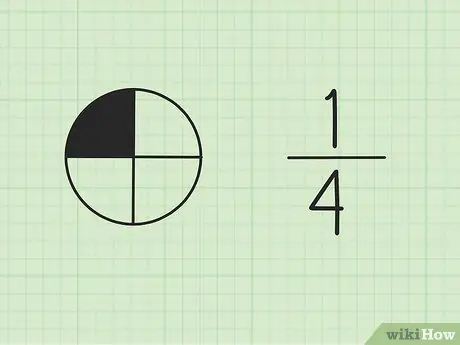
Step 1. Understand that fractions are part of a whole
The number at the top is called the numerator, and represents the number of parts of the total. The number at the bottom is called the denominator, which represents the total number of parts.
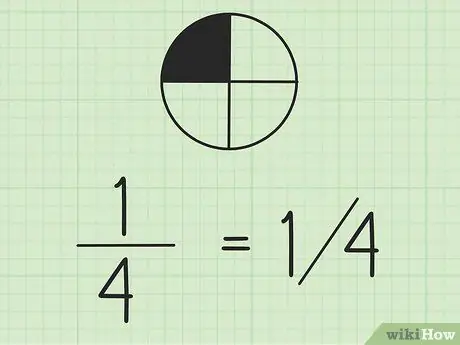
Step 2. Keep in mind that you can write fractions using slashes
The number on the left is the numerator and the number on the right is the denominator. If you're working with fractions on the same line, it's a good idea to write the numerator above the denominator.
For example, if you take one of four pizza slices, you have pizza. If you have 7/3 pizzas, that means you have two whole pizzas plus 1 of 3 pizza slices
Method 2 of 5: Difference between Mixed and Simple Fractions

Step 1. Understand that mixed numbers consist of whole numbers and fractions, for example 2 1/3 or 45 1/2
Usually, you have to convert mixed numbers to a simpler form to add, subtract, multiply, or divide.

Step 2. Change the mixed number by multiplying the whole number by the denominator in the fraction, then adding it by the numerator
Write the result as the numerator, while the denominator does not change.
For example, to convert 2 1/3 to a simple fraction, multiply 2 by 3, then add 1 and get 7/3

Step 3. Convert simple fractions to mixed numbers by dividing the numerator by the denominator
The whole result of the division is written as an integer, and the remainder of the division is written as the numerator of the fraction. The denominator does not change.
For example, to convert 7/3 to a mixed number, divide 7 by 3 to get 2 with a remainder of 1. So the mixed number is 2 1/3. Simple fractions can only be converted to mixed numbers if the numerator is greater than the denominator
Method 3 of 5: Adding and Subtracting Fractions

Step 1. Find a common denominator to add and subtract fractions
The trick, multiply the numbers in the denominator, then multiply each numerator by the number used to find the denominator. Sometimes, you can find the LCM (least common multiple) for the denominator by multiplying the denominators by each other.
For example, to add and 1/3, first find the LCM (least common multiple) of the two denominators by multiplying each other. Thus, you multiply 2 and 3 to get LCM 6. Multiply 1 by 3 to get 3 as the new numerator of the first fraction. Multiply 1 by 2 to get 2 as the new numerator of the second fraction. Your new fractions are 3/6 and 2/6
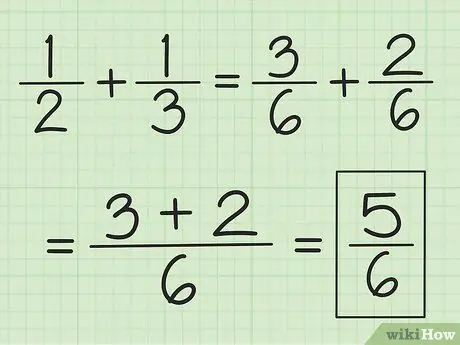
Step 2. Add the two numerators together and don't change the denominator
For example, 3/6 plus 2/6 is 5/6, and 2/6 plus 1/6 is 3/6
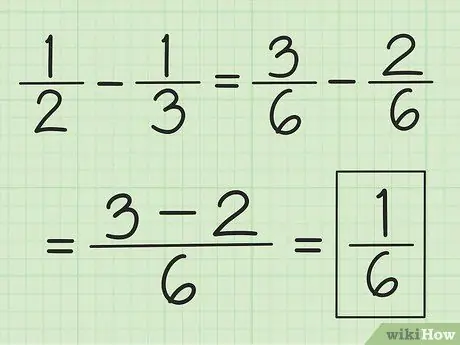
Step 3. Use a similar technique for subtraction
Find the LCM of the denominators first, but instead of adding them up, subtract the number of the first numerator by the number of the second.
For example, to subtract 1/3 from 1/2, first change the fractions to 3/6 and 2/6, then subtract 3 by 2 to get 1. This results in 1/6
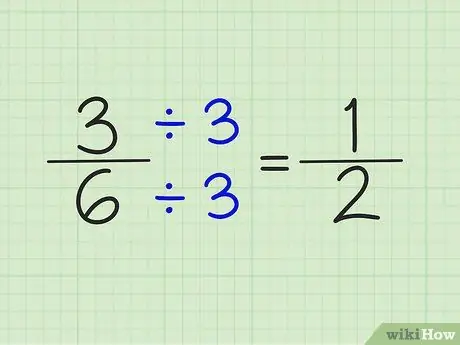
Step 4. Simplify fractions by dividing the numerator and denominator by the same number
For example, the number 5/6 cannot be simplified. However, 3/6 can be simplified by dividing the numerator and denominator by the number 3. The result is a fraction of 1/2

Step 5. Convert the fraction to a mixed number if the numerator is greater than the denominator
Method 4 of 5: Multiply and Divide Fractions
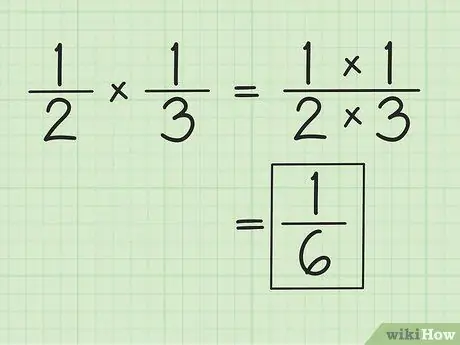
Step 1. Multiply the numerator and denominator separately to multiply fractions
For example, when multiplying and 1/3, the result is 1/6 (1 times 1, and 2 times 3). You don't need to match the denominators when multiplying fractions. Simplify or modify the results obtained, if necessary
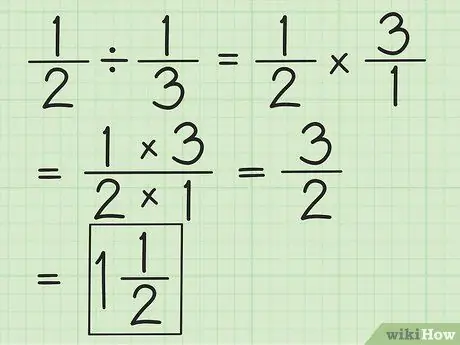
Step 2. Divide two fractions by inverting the second fraction, then multiplying both
For example, if you want to divide 1/2 by 1/3, first reverse the second fraction to 3/1. Multiply by 3/1 and get 3/2. Simplify fractions or convert them to mixed numbers, if possible
Method 5 of 5: Working with Complex Fractions
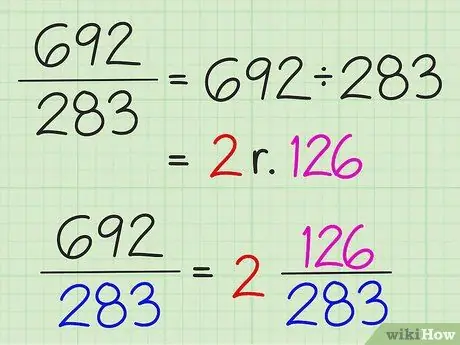
Step 1. Work all the fractions the same way, even if the problem seems very complicated
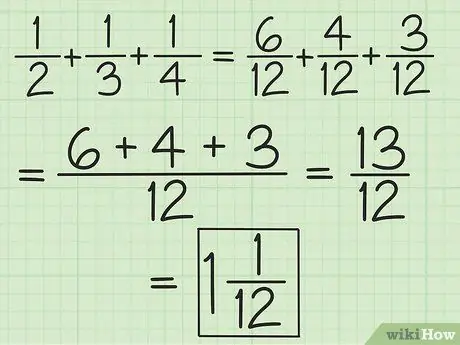
Step 2. Match the denominators for all fractions or work in pairs starting from left to right to add and subtract more than two fractions
For example, to add up 1/2, 1/3 and 1/4, you can change them to 6/12, 4/12, and 3/12 to get 13/12, or you can add 3/6 and 2/6 so you get 5/6, then add 5/6 and 1/4 (equalize the denominators so the second fraction becomes 3/12) to get 13/12 (10/12 plus 3/12). Convert it to a mixed number, which is 1 1/12
Tips
- Remember that you have learned quite a lot of math. Mathematics is like a language that you can pronounce fluently, and now you are trying to learn to read and write it.
- Remember to always simplify the final result of your calculations, whether your problem is in the form of an ordinary fraction, a mixed number, or a complex fraction.






