- Author Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Last modified 2025-01-23 12:04.
The center of gravity (CG) is the center of the weight distribution of an object when the center of gravity can be considered as a force. This is the point at which the object is in perfect balance, regardless of how the object is rotated or flipped at that point. If you want to find the value of the center of gravity of an object, you first need to know the value of the weight of the object, and the objects on it, the location of the datum, and plug the values into the equation to calculate the center of gravity. Read this article to learn more about it
Step
Method 1 of 4: Determining the Weight of the Object
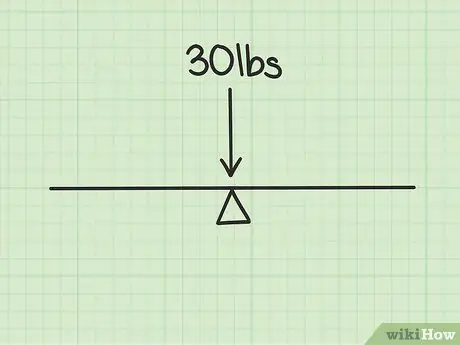
Step 1. Calculate the weight of an object
When you calculate the center of gravity, the first thing you need to do is find the weight of the object. Say you calculated the weight of a seesaw with a weight of 30 kg. Since this object is symmetrical and no one is climbing on it, the object's center of gravity will be exactly in the middle. However, if the seesaw was climbed by people at both ends, the matter would become a little more complicated.

Step 2. Calculate the additional weight
To find the center of gravity of the seesaw that two children are riding, you need the weight of each child. For example, the first child weighs 40 kg and the second child weighs 60 kg.
Method 2 of 4: Determining the Datum
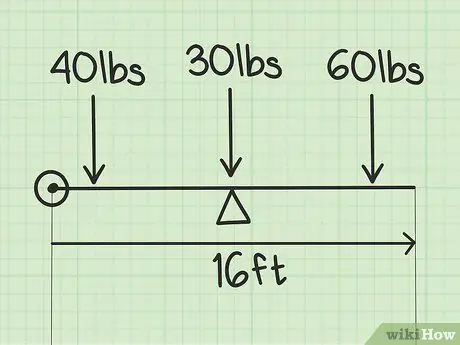
Step 1. Choose a datum
A datum is an arbitrary starting point placed at one end of the seesaw. Let's say the seesaw is 16 meters long. Place the datum on the left side of the seesaw, close to the first child.
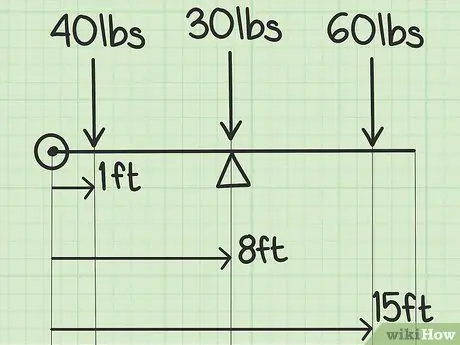
Step 2. Measure the datum distance from the center of the main object as well as from the two additional weights
Say each child sits 1 meter from the tip of the seesaw. The center of gravity is in the middle of the seesaw, which is 8 meters because 16 meters divided by 2 is 8. Here are the distances from the main object and the two additional objects that make up the datum:
- The center of the seesaw = 8 meters from the datum.
- Child 1 = 1 meter away from datum.
- Child 2 = 15 meters from the datum
Method 3 of 4: Finding the Center of Gravity

Step 1. Multiply each object's distance from the datum by its weight to find the moment value
Thus, you get the moment of each object. Here's how to multiply an object's weight by each object's distance from its datum:
- Seesaw: 30 kg x 8 meters = 240 kg x m.
- Child 1 = 40 kg x 1 meter = 40 kg x m
- Child 2 = 60 kg x 15 m = 900 kg x m

Step 2. Add up the three moments
Just calculate 240 kg x m + 40 kg x m + 900 kg x m = 1,180 kg x m. The total moment is 1,180 kg x m.

Step 3. Add the weight of all objects
Find the total weight of the seesaw, first child, and second child. Thus: 30 kg + 40 kg + 60 kg = 130 kg.
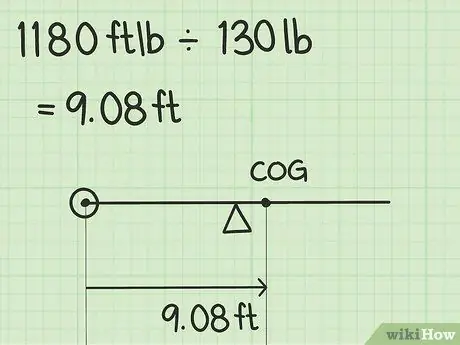
Step 4. Divide the total moment by the total weight
Thus, you obtain the distance from the datum to the object's center of gravity. To do this, divide 1,180 kg x m by 130 kg.
- 1,180 kg x m 130 kg = 9.08 meters
- The seesaw's center of gravity is 9.08 from the datum location, i.e. from the left end of the seesaw.
Method 4 of 4: Checking Answers
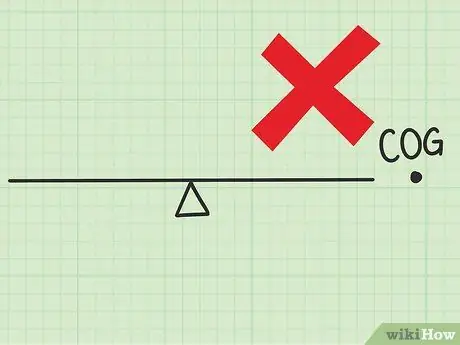
Step 1. Find the center of gravity in the diagram
If the center of gravity found is outside the object system, your answer is likely wrong. Perhaps you have measured the distance to more than one point. Try again with one datum.
- For example, for a person on a seesaw, the center of gravity should be on the seesaw, not on the left or right of the seesaw. It doesn't have to be exactly on someone.
- This applies to two-dimensional problems. Draw a square large enough to hold all the objects in the problem. The center of gravity must be inside this square.

Step 2. Check your calculations if the answer value is too small
If you select one end of the system as the datum, the small answer places the center of gravity exactly at one end. This answer may be correct, but is often a sign of the wrong answer. When calculating moments, do you “multiply” the weight and distance? This is the correct way to find the moment value. If you "add them up" instead, the answer is usually smaller.
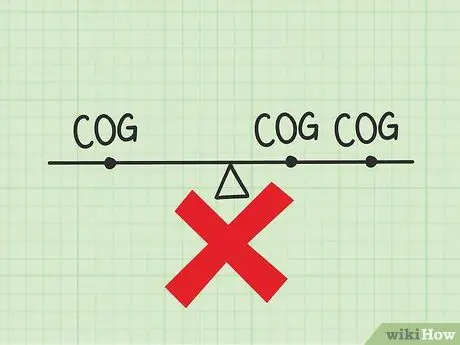
Step 3. Solve the problem if you have more than one center of gravity
Each system has only one center of gravity. If you get more than one answer, chances are you missed the step to add up all the moments in the object. The center of gravity is the “total” moment divided by the “total” weight. You don't need to divide “every” moment by “every” weight, which simply shows the position of each object.

Step 4. Check the datum if your answer misses some whole numbers
Say the correct answer is 9.08 meters, and the answer you get is 1.08 m, 7.08 m, or any number ending in “, 08”. This often happens because we select the left side as the datum, while you choose the right edge of the seesaw. Your answer is actually “correct”, no matter what datum is chosen! You just need to remember datum is always at x = 0. Here's an example:
- According to the method in this article, the datum is on the left side of the seesaw. Our answer is 9.08 meters so the center of gravity is 9.08 from the datum at the left end of the seesaw.
- If you select a datum at 1 meter from the left end of the seesaw, the answer obtained is 8.08 meters. The center of gravity is 8.08 meters from the new datum, which is 1 meter from the left end of the seesaw. The center of gravity is 8.08 + 1 = 9.08 meters from the far left, and is the same answer from before.
- (Note: When measuring distance, do not forget that the distance next to left' datum is negative, and the distance next to right datum is positive.)
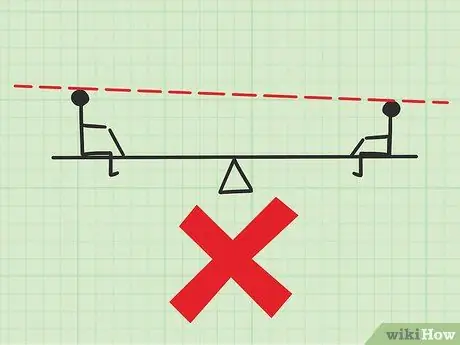
Step 5. Make sure all your sizing information is in a straight line
Say you saw another example of "children playing on a seesaw," but one of the children is taller than the other, or is hanging under the seesaw instead of sitting on it. Ignore this difference and take all the sizing information along the straight line of the seesaw. Measuring distance using angles will yield an answer that is almost right but slightly off.
For the seesaw problem, all you need to pay attention to is whether the center of gravity is on the left or right side of the seesaw. Later, you will learn more sophisticated ways to calculate the center of gravity in two dimensions
Tips
- To find the distance it takes a person to move to balance at the fulcrum of the seesaw, use the formula: (weight transferred) / (total weight) = (distance to center of gravity) / (distance to weight transfer). This formula can be rewritten to show the distance the weight (person) has moved is equal to the distance between the center of gravity and the fulcrum times the weight of the person divided by the total weight. So, the first child needs to move -1.08 meters * 40 kg / 130 kg = -0.33 meters (towards the edge of the seesaw). Alternatively, the second child must move -1.08 meters * 130 kg / 60 kg = -2.33 meters (towards the center of the seesaw).
- To find the center of gravity of a two-dimensional object, use the formula Xcg = xW/∑W to find the center of gravity along the X axis, and Ycg = yW/∑W to find the center of gravity along the Y axis. The point of intersection of the two is the center of gravity. object.
- The definition of the center of gravity of the general mass distribution is (∫ r dW/∫ dW) where dW is the weight difference, r is the position vector and the integral is called the Stieltjes integral over the body. However, you can express it as a more conventional Riemann or Lebesgue volume integral for distributions that admit the density function. Starting from this definition, all properties of the center of gravity, including those used in this article, can be derived from the Stieltjes integral property.






