- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-01-23 12:04.
Gravity is one of the fundamental forces in physics. The most important aspect of gravity is that it is universal: all objects have a gravitational force that attracts other objects. The magnitude of the gravitational force depends on the mass and the distance between the two objects.
Step
Part 1 of 2: Calculating the Force of Gravity Between Two Objects

Step 1. Define the equation for the gravitational force pulling on an object, Fgrav = (Gm1m2)/d2.
To be able to calculate the gravitational force of an object, this equation also takes into account the masses of the two objects and their distance from each other. The equation variables are described below.
- Fgrav is the gravitational force
- G is the universal gravitation constant 6.673 x 10-11 Nm2/kg2
- m1 is the mass of the first object
- m2 is the mass of the second object
- d is the distance between the centers of the two objects
- Sometimes you find the letter r instead of d. These two symbols represent the distance between the two objects.

Step 2. Use the appropriate metric units
For this equation, you must use metric units. The mass of the object must be in kilograms (kg) and the distance between the objects must be in meters (m). You must convert these units to metric units before proceeding

Step 3. Determine the mass of the object in question
For small objects, you can weigh them to find out their weight in kilograms. For large objects, you can look up the approximate mass on a table or on the internet. In physics problems, usually the mass of the object will be told.

Step 4. Measure the distance between the two objects
If you are trying to calculate the gravitational force between an object and the earth, you need to know how far this object is from the center of the earth.
- The distance from the earth's surface to the center of the earth is about 6.38 x 106 m.
- You can look up tables or other sources on the internet that tell you the approximate distance from the center of the earth to objects at various heights on the earth's surface.

Step 5. Complete the calculation
If you have defined the variables in the equation, feel free to enter them to solve. Make sure all variables are in metric units and are properly scaled. Mass must be in kilograms and distance must be in meters. Solve equations in the correct order of calculations.
- For example, determine the gravitational force of a person whose mass is 68 kg above the earth's surface. Earth's mass is 5.98 x 1024 kg.
- Make sure all variables are in correct units. m1 = 5, 98 x 1024 kg, m2 = 68 kg, G = 6.673 x 10-11 Nm2/kg2, and d = 6, 38 x 106 m
- Write your equation: Fgrav = (Gm1m2)/d2 = [(6, 67 x 10-11) x 68 x (5, 98 x 1024)]/(6, 38 x 106)2
- Multiply the masses of the two objects that are taken into account. 68 x (5, 98 x 1024) = 4.06 x 1026
- Multiply the result m1 and m2 with the gravitational constant G. (4.06 x 1026) x (6.67 x 10-11) = 2,708 x 1016
- Square the distance between the two objects. (6, 38 x 106)2 = 4.07 x 1013
- Share result G x m1 x m2 by the distance squared to obtain the gravitational force in Newtons (N). 2, 708 x 1016/4, 07 x 1013 = 665 N
- Its gravitational force is 665 N.
Part 2 of 2: Calculating the Force of Gravity on Earth

Step 1. Understand Newton's Second Law, F = ma
Newton's second law states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. In other words, if a force acting on an object is greater than the force acting in the opposite direction, the object will move with the stronger force.
- This law can be summed up by the equation F = ma, where F is the force, m is the mass of the object, and a is the acceleration.
- Thanks to this law, we can calculate the gravitational force of all objects on the earth's surface, using the known acceleration due to gravity.
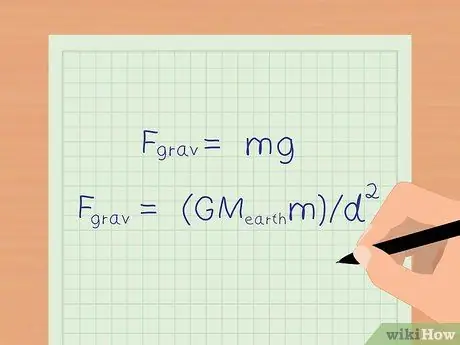
Step 2. Find the acceleration due to Earth's gravity
On earth, the force of gravity causes all objects to accelerate by 9.8 m/s2. At the earth's surface, we can use a simplified equation: Fgrav = mg to calculate the gravitational force.
If you want to know a more precise number of gravitational forces, you can still use the formula in the previous step, Fgrav = (GMEarthm)/d2 to determine the gravitational force.

Step 3. Use the appropriate metric units
For this equation, you must use metric units. The mass of the object must be in kilograms (kg) and the distance between the objects must be in meters (m). You must convert these units to metric units before proceeding.

Step 4. Determine the mass of the object in question
For small objects, you can weigh them to find out their weight in kilograms. For large objects, you can look up the approximate mass on a table or on the internet. In physics problems, usually the mass of the object will be told.

Step 5. Complete the calculation
If you have defined the variables in the equation, feel free to enter them to solve. Make sure all variables are in metric units and are properly scaled. Mass must be in kilograms and distance must be in meters. Solve equations in the correct order of calculations.
- Let's try using the equation in the previous step and see how close the results are. Determine the gravitational force of a person with a mass of 68 kg on the earth's surface.
- Make sure all variables are in correct units: m = 68 kg, g = 9.8 m/s2.
- Write down the formula. Fgrav = mg = 68*9, 8 = 666 N.
- Using the formula F = mg the gravitational force is 666 N, while the result from the formula in the previous step is 665 N. As you can see, the two results are almost the same.
Tips
- These two formulas should give the same answer, but the shorter and simpler formula is easier to use when discussing objects on the surface of a planet.
- Use the first formula if you don't know the acceleration due to gravity on a planet, or you're calculating the gravitational force between two very large objects, such as the moon or planets.






