- Author Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Last modified 2025-06-01 06:05.
Hypothesis testing is done by statistical analysis. Statistical significance was calculated using the p-value, which indicates the magnitude of the probability of the research results, provided that certain statements (zero hypothesis) are true. If the p value is less than the predetermined significance level (generally 0.05), the researcher can conclude that the null hypothesis is not true and accept the alternative hypothesis. Using a simple t-test, you can calculate a p-value and determine the significance between two different sets of data.
Step
Part 1 of 3: Setting Up Experiments

Step 1. Establish a hypothesis
The first step in analyzing statistical significance is to determine the research question you wish to answer and formulate your hypothesis. A hypothesis is a statement about your experimental data and explains possible differences in the study population. For each experiment, a null hypothesis and an alternative hypothesis must be established. Generally, you will compare two groups to see if they are the same or different.
- The null hypothesis (H0) generally states that there is no difference between the two data sets. Example: the group of students who read the material before class started did not get better grades than the group who did not read the material.
- Alternative hypothesis (Ha) is a statement that contradicts the null hypothesis and one that you are trying to support with experimental data. Example: the group of students who read the material before class got better grades than the group that did not read the material.

Step 2. Limit the level of significance to determine how unique your data must be for it to be considered significant
The level of significance (alpha) is the threshold used to determine the significance. If the p value is less than or equal to the level of significance, the data is considered statistically significant.
- As a general rule, the significance level (alpha) is set at 0.05, meaning that the probability of both groups of data being equal is only 5%.
- By using a higher level of confidence (lower p value) means that the experimental results will be considered more significant.
- If you want to increase the confidence level of your data, lower the p-value more to 0.01. Lower p-values are commonly used in manufacturing when detecting product defects. A high level of confidence is essential to ensure that every manufactured part performs its function.
- For hypothesis testing experiments, a significance level of 0.05 is acceptable.
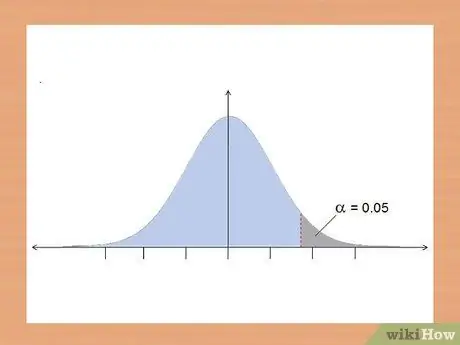
Step 3. Decide to use a one-tailed test or a two-tailed test
One of the assumptions used when you perform a t-test is that your data is normally distributed. Data that is normally distributed will form a bell curve with most of the data being in the middle of the curve. The t-test is a mathematical test used to see if your data is outside the normal distribution, below or above the "tail" of the curve.
- If you are not sure your data is below or above the control group, use a two-tailed test. This test will check the significance of both directions.
- If you know the direction of the trend of your data, use a one-sided test. Using the previous example, you expected that a student's grade would increase. Therefore, you should use a one-tailed test.
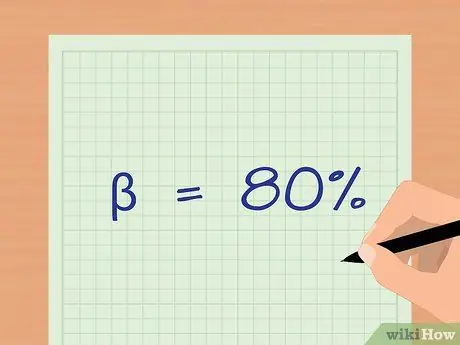
Step 4. Determine the sample size by test-statistical power analysis
The power of test-statistics is the probability that a certain statistical test can give the correct result, with a certain sample size. The test power threshold (or) is 80%. Analysis of the strength of a statistical test can be complicated without preliminary data because you will need information about the estimated mean of each data set and its standard deviation. Use the online statistical test power analysis calculator to determine the optimal sample size for your data.
- Researchers generally conduct pilot studies as a material for statistical-test strength analysis and as a basis for determining the sample size needed for larger and more comprehensive studies.
- If you do not have the resources to conduct a pilot study, estimate the mean based on the literature and other research that has been done. This method will provide information to determine the sample size.
Part 2 of 3: Calculating the Standard Deviation
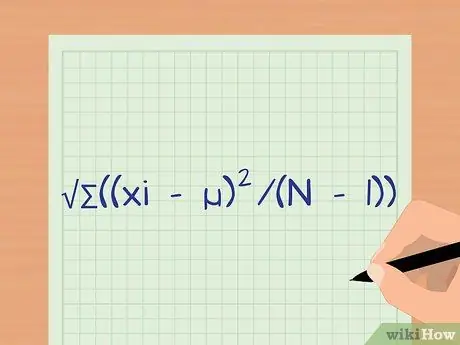
Step 1. Use the standard deviation formula
The standard deviation (also known as the standard deviation) is a measure of the distribution of your data. The standard deviation provides information about the similarity of each data point in your sample. At first, the standard deviation equation may seem complicated, but the steps below will help with your calculation process. The standard deviation formula is s = ((xi -)2/(N - 1)).
- s is the standard deviation.
- means that you have to add up all the sample values that you have collected.
- xi represents all the individual values of your data points.
- is the average of the data for each group.
- N is the number of your samples.

Step 2. Calculate the sample mean in each group
To calculate the standard deviation, you must first calculate the sample mean in each data set. The average is denoted by the Greek letter mu or. To do this, add up all the sample data point values and divide by the number of your samples.
- For example, to get the average score of the group of students who read the material before class, let's look at the sample data. For simplicity, we will use 5 data points: 90, 91, 85, 83, and 94.
- Add up all sample values: 90 + 91 + 85 + 83 + 94 = 443.
- Divide by the number of samples, N = 5:443/5 = 88, 6.
- The average score for this group was 88. 6.

Step 3. Subtract each sample data point value by the average value
The second step is to complete the part (xi -) equation. Subtract each sample data point value from the pre-calculated mean. Continuing the previous example, you have to do five subtractions.
- (90 - 88, 6), (91- 88, 6), (85 - 88, 6), (83 - 88, 6), and (94 - 88, 6).
- The values obtained are 1, 4, 2, 4, -3, 6, -5, 6, and 5, 4.

Step 4. Square each value that has been obtained and add up all of them
Square each value you just calculated. This step will remove the negative numbers. If there is a negative value after this step is performed or the time after all calculations have been performed, you may have forgotten this step.
- Using the previous example, we get the values 1, 96, 5, 76, 12, 96, 31, 36, and 29.16.
- Add up all the values: 1, 96 + 5, 76 + 12, 96 + 31, 36 + 29, 16 = 81, 2.
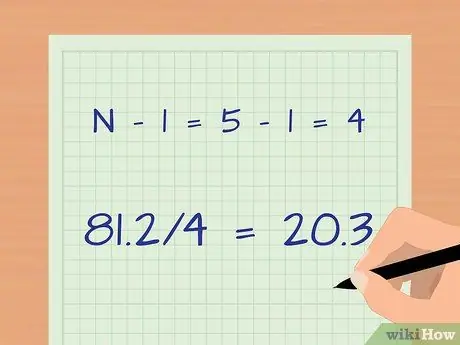
Step 5. Divide by the number of samples minus 1
The formula expresses N - 1 as an adjustment because you are not counting the entire population; You only take a sample of the population to make an estimate.
- Subtract: N - 1 = 5 - 1 = 4
- Divide: 81, 2/4 = 20, 3
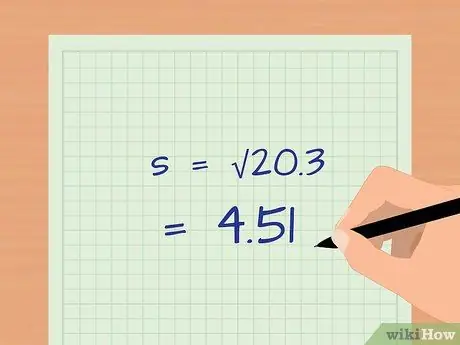
Step 6. Calculate the square root
After you divide by the number of samples minus one, calculate the square root of the final value. This is the final step to calculate the standard deviation. There are several statistical programs that can calculate the standard deviation after you've entered the raw data.
For example, the standard deviation of the scores for the group of students who read the material before class starts is: s =√20, 3 = 4, 51
Part 3 of 3: Determining Significance

Step 1. Calculate the variance between the two sample groups
In the previous example, we only calculated the standard deviation of one group. If you want to compare two groups, you should have data from the two groups. Calculate the standard deviation of the second group and use the results to calculate the variance between the two groups in the experiment. The formula for variance is sd = ((s1/N1) + (s2/N2)).
- sd is the intergroup variance.
- s1 is the standard deviation of group 1 and N1 is the number of samples in group 1.
- s2 is the standard deviation of group 2 and N2 is the number of samples in group 2.
-
For example, data from group 2 (students who do not read the material before class starts) has a sample size of 5 with a standard deviation of 5.81. Then the variant:
- sd = ((s1)2/N1) + ((s2)2/N2))
- sd = √(((4.51)2/5) + ((5.81)2/5)) = √((20.34/5) + (33, 76/5)) = √(4, 07 + 6, 75) = √10, 82 = 3, 29.

Step 2. Calculate the t-test value of your data
The t-test value will allow you to compare one group of data with another group of data. The t-value allows you to perform a t-test to determine how much the probability that the two groups of data being compared are significantly different. The formula for the value of t is: t = (µ1 -2)/sd.
- ️1 is the mean of the first group.
- ️2 is the average value of the second group.
- sd is the variance between the two samples.
- Use the larger mean as1 so you don't get negative values.
- For example, the mean score of group 2 (students who do not read) is 80. The t-value is: t = (µ1 -2)/sd = (88, 6 - 80)/3, 29 = 2, 61.
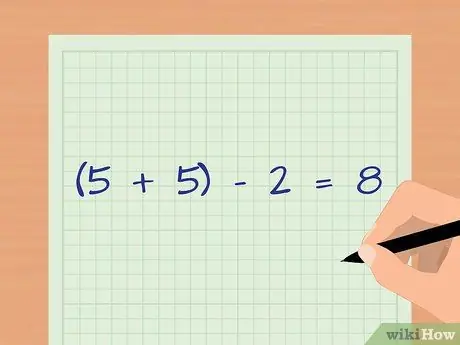
Step 3. Determine the degrees of freedom of the sample
When using the t-value, the degrees of freedom are determined by the size of the sample. Add the number of samples from each group then subtract two. For example, the degrees of freedom (d.f.) are 8 because there are five samples in the first group and five samples in the second group ((5 + 5) - 2 = 8).

Step 4. Use Table t to determine significance
Tables of t-values and degrees of freedom can be found in standard statistics books or online. Look at the row showing the degrees of freedom you selected for your data and find the appropriate p-value for the t-value derived from your calculations.
With degrees of freedom of 8 d.f. and the t-value of 2.61, the p-value for the one-tailed test is between 0.01 and 0.025. Since we used a significance level of less than or equal to 0.05, the data we use prove that the two data groups are significantly different. significant. With this data, we can reject the null hypothesis and accept the alternative hypothesis: the group of students who read the material before class started scored better than the group of students who did not read the material

Step 5. Consider doing a follow-up study
Many researchers conduct small pilot studies to help them understand how to design larger studies. Doing further research with more measurements will increase your confidence in your conclusions.






