- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-01-23 12:04.
Velocity is defined as the speed of an object in a certain direction. In many situations, to find velocity, we can use the equation v = s/t, where v equals velocity, s equals the total distance the object has moved from its initial position, and t equals time. However, this method only gives the "average" velocity value of the object over its displacement. Using calculus, you can calculate the velocity of an object at any point along its displacement. This value is called the "instant velocity" and can be calculated by the equation v = (ds)/(dt), or, in other words, is the derivative of the equation for the average velocity of the object.
Step
Method 1 of 3: Calculating Instantaneous Speed

Step 1. Start with the equation for the velocity of the object's displacement
To get the value of the instantaneous velocity of an object, we must first have an equation that describes its position (in terms of its displacement) at a given point in time. This means that the equation must have a variable s (which stands alone) on one side, and t on the other hand (but not necessarily standalone), like this:
s = -1.5t2+10t+4
-
In the equation, the variables are:
-
-
Displacement = s. That is the distance traveled by the object from its starting point. For example, if an object travels 10 meters forward and 7 meters back, then the total distance traveled is 10 - 7 = 3 meters (not 10 + 7 = 17 meters).
-
Time = t. This variable is self-explanatory. Usually expressed in seconds. # Take the derivative of the equation. The derivative of an equation is another equation that can give the slope value from a certain point. To find the derivative of the formula for the displacement of an object, derive the function using the following general rule: If y = a*x , Derivative = a*n*xn-1. This rule applies to any component that is on the "t" side of the equation.

Calculate Instantaneous Velocity Step 2
-
-
- In other words, start by descending the "t" side of the equation from left to right. Each time you reach the "t" value, subtract 1 from the exponent value and multiply the whole by the original exponent. Any constants (variables that do not contain "t") will be lost because they are multiplied by 0. This process is not as difficult as one might think, let's derive the equation in the step above as an example:
s = -1.5t2+10t+4
(2)-1.5t(2-1)+ (1)10t1 - 1 + (0)4t0
-3t1 + 10t0
-3t + 10

Step 2. Replace the variable "s" with "ds/dt
"To show that your new equation is the derivative of the previous equation, replace "s" with "ds/dt". Technically, this notation means "derivative of s with respect to t." A simpler way to understand this is that ds/dt is the value of the slope (slope) at any point in the first equation, for example, to determine the slope of a line drawn from the equation s = -1.5t2 + 10t + 4 at t = 5, we can plug the value "5" into the derivative equation.
- In the example used, the first derivative equation would now look like this:
ds/sec = -3t + 10

Step 3. Plug the value of t into the new equation to get the instantaneous velocity value
Now that you have the derivative equation, it's easy to find the instantaneous velocity at any point. All you need to do is pick a value for t and plug it into your derivative equation. For example, if you want to find the instantaneous velocity at t = 5, you can replace the value of t with "5" in the derivative equation ds/dt = -3 + 10. Then solve the equation like this:
ds/sec = -3t + 10
ds/sec = -3(5) + 10
ds/sec = -15 + 10 = -5 meters/second
Note that the unit used above is "meter/second". Because what we calculate is displacement in meters and time in seconds (seconds) and velocity in general is displacement in a certain time, this unit is appropriate to use
Method 2 of 3: Graphically Estimating Instantaneous Speed
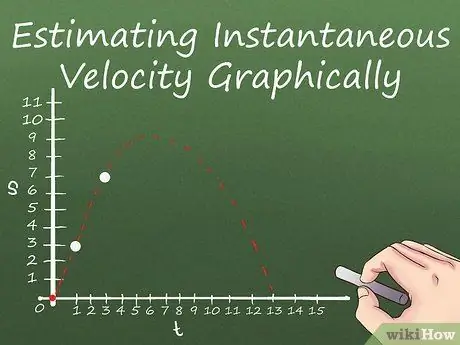
Step 1. Draw a graph of the object's displacement over time
In the above section, the derivative is mentioned as the formula for finding the slope at a given point for the equation you are deriving. In fact, if you represent an object's displacement as a line on a graph, "the slope of the line at all points is equal to the value of its instantaneous velocity at that point."
- To describe the displacement of an object, use x to represent time and y to represent displacement. Then draw the points, plugging the value of t into your equation, thus getting the value of s for your graph, mark t, s in the graph as (x, y).
- Note that your graph can span below the x-axis. If the line representing the movement of your object reaches the bottom of the x-axis, then this means that the object has moved backwards from its initial position. In general, your graph won't reach the back of the y-axis - because we're not measuring the speed of an object moving past!
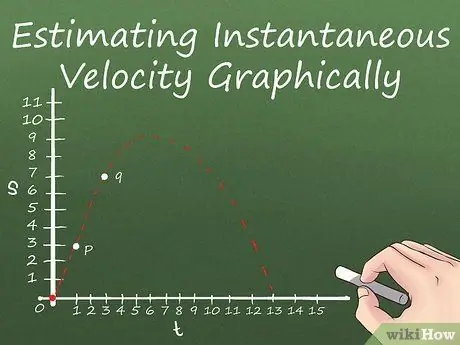
Step 2. Select an adjacent point P and Q in the line
To get the slope of the line at a point P, we can use a trick called "taking the limit." Taking the limit involves two points (P and Q, a point nearby) on the curved line and finding the slope of the line by connecting them many times until the distances P and Q get closer.
Let's say the object's displacement line contains the values (1, 3) and (4, 7). In this case, if we want to find the slope at the point (1, 3), we can determine (1, 3) = P and (4, 7) = Q.

Step 3. Find the slope between P and Q
The slope between P and Q is the difference in y values for P and Q along the x-axis value difference for P and Q. In other words, H = (yQ - yP)/(xQ - xP), where H is the slope between the two points. In our example, the value of the slope between P and Q is
H = (yQ- yP)/(xQ- xP)
H = (7 - 3)/(4 - 1)
H = (4)/(3) = 1.33
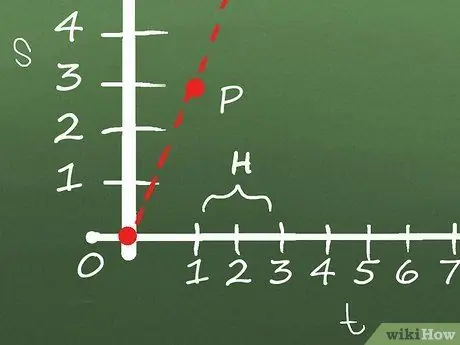
Step 4. Repeat several times, moving Q closer to P
Your goal is to reduce the distance between P and Q to resemble a dot. The closer the distance between P and Q, the closer the slope of the line at point P. Do this several times with the equation used as an example, using points (2, 4.8), (1.5, 3.95), and (1.25, 3.49) as Q and the starting point (1, 3) as P:
Q = (2, 4.8):
H = (4.8 - 3)/(2 - 1)
H = (1.8)/(1) = 1.8
Q = (1.5, 3.95):
H = (3.95 - 3)/(1.5 - 1)
H = (.95)/(.5) = 1.9
Q = (1.25, 3.49):
H = (3.49 - 3)/(1.25 - 1)
H = (.49)/(.25) = 1.96

Step 5. Estimate the slope of the line for a very small distance
As Q gets closer to P, H gets closer and closer to the value of the slope of the point P. Eventually, when it reaches a very small value, H equals the slope of P. Since we cannot measure or calculate very small distances, we can only estimate the slope on P after clear from the point we are trying.
- In the example, as we move Q closer to P, we get values of 1.8, 1.9, and 1.96 for H. Since these numbers are close to 2, we can say that 2 is the approximate slope of P.
- Remember that the slope at a given point on the line is equal to the derivative of the equation of the line. Since the line used shows the displacement of an object over time, and because as we saw in the previous section, the instantaneous velocity of an object is the derivative of its displacement at a given point, we can also state that "2 meters/second" is the approximate value of the instantaneous velocity at t = 1.
Method 3 of 3: Sample Questions

Step 1. Find the value of the instantaneous velocity at t = 4, from the displacement equation s = 5t3 - 3t2 +2t+9.
This problem is the same as the example in the first part, except that this equation is a cube equation, not a power equation, so we can solve this problem in the same way.
- First, we take the derivative of the equation:
- Then, enter the value of t(4):
s = 5t3- 3t2+2t+9
s = (3)5t(3 - 1) - (2)3t(2 - 1) + (1)2t(1 - 1) + (0)9t0 - 1
15t(2) - 6t(1) + 2t(0)
15t(2) - 6t + 2
s = 15t(2)- 6t + 2
15(4)(2)- 6(4) + 2
15(16) - 6(4) + 2
240 - 24 + 2 = 22 meters/second

Step 2. Use a graphical estimate to find the instantaneous velocity at (1, 3) for the displacement equation s = 4t2 - t.
For this problem, we will use (1, 3) as point P, but we must define another point adjacent to that point as point Q. Then we just need to determine the value of H and make an estimate.
- First, find the value of Q first at t = 2, 1.5, 1.1 and 1.01.
- Then, determine the value of H:
- Since the value of H is very close to 7, we can state that 7 meters/secondis the approximate instantaneous velocity at (1, 3).
s = 4t2- t
t = 2:
s = 4(2)2- (2)
4(4) - 2 = 16 - 2 = 14, so Q = (2, 14)
t = 1.5:
s = 4(1.5)2 - (1.5)
4(2.25) - 1.5 = 9 - 1.5 = 7.5, so Q = (1.5, 7.5)
t = 1.1:
s = 4(1.1)2 - (1.1)
4(1.21) - 1.1 = 4.84 - 1.1 = 3.74, so Q = (1.1, 3.74)
t = 1.01:
s = 4(1.01)2 - (1.01)
4(1.0201) - 1.01 = 4.0804 - 1.01 = 3.0704, so Q = (1.01, 3.0704)
Q = (2, 14):
H = (14 - 3)/(2 - 1)
H = (11)/(1) =
Step 11.
Q = (1.5, 7.5):
H = (7.5 - 3)/(1.5 - 1)
H = (4.5)/(.5) =
Step 9.
Q = (1.1, 3.74):
H = (3.74 - 3)/(1.1 - 1)
H = (.74)/(.1) = 7.3
Q = (1.01, 3.0704):
H = (3.0704 - 3)/(1.01 - 1)
H = (.0704)/(.01) = 7.04
Tips
- To find the value of acceleration (change in velocity over time), use the method in the first section to obtain the derivative equation of the displacement function. Then create the derived equation again, this time from your derived equation. This will give you the equation to find the acceleration at any given time, all you have to do is enter your time value.
- The equation relating the value of Y (displacement) to X (time) may be very simple, for example Y= 6x + 3. In this case, the slope value is constant, and there is no need to find the derivative to calculate it, where according to the equation of a straight line, Y = mx + b will equal 6.
- Displacement is similar to distance, but has a direction, so displacement is a vector quantity, while distance is a scalar quantity. The displacement value can be negative, but the distance will always be positive.






