- Author Jason Gerald [email protected].
- Public 2024-01-16 19:04.
- Last modified 2025-01-23 12:04.
Speed is a calculation of how fast something is moving at one time. If you've ever looked at the speedometer of a moving car, you'll see the speed count - the farther the needle travels, the higher the speed of the vehicle. There are several ways to calculate speed, depending on the type of information you have. In general, the formula speed = distance/time (or k = j/w) is the easiest way to calculate speed.
Step
Method 1 of 3: Using Standard Speed Calculation Formulas

Step 1. Find the distance an object has traveled
The basic formula that most people use to find the speed of something is very easy to use. First of all, you need to know “how much distance has the measured object traveled”. In other words, what is the distance between the starting point and the end point of the object?
This formula is easier to understand through an example. Let's say that we travel by car to a playground for "161 kilometers". In a few steps, we can use this information to complete the calculation of the above formula

Step 2. Find the time it takes the object to travel that distance
The next information you need is how long it takes the object to reach a certain distance. In other words, how long does it take for the object to move from the start point to the end point?
In this example, let's say the object takes approx. two hours to get to the destination.

Step 3. Divide the distance by the time taken to find the object's velocity
You only need these two pieces of information to know the speed of the object. The distance to time is equal to the object's velocity.
In this example, 161 kilometers/2 hours = 80.5 kilometers/hour.

Step 4. Don't forget the unit used
It is very important to use the correct units in your answer (such as kilometers per hour, etc.) Without these units, it is very difficult for people to understand the meaning of your answer. You can also lose points if you use the wrong unit when doing assignments from school.
The unit of speed is unit of distance to unit of time. For example, since we measure distance in kilometers and time in hours, the units used are kilometers/hour (or kilometers per hour).
Method 2 of 3: Solving More Difficult Calculations

Step 1. Find several different variables to solve the problem of distance and time
Once you understand the basic formula for speed, you can use it to perform calculations other than speed. For example, if at first you only know the velocity of the object and one other variable, you can rearrange the formula above to find the unknown information.
-
For example, let's say that we know that a train travels at 20 kilometers per hour for four hours, but we don't know how far it has traveled. To find out, we can rearrange the formula in the following way:
-
- speed = distance/time
- speed × time = (distance/time) × time
- speed × time = distance
- 20 km/hour × 4 hours = distance = 80 kilometers
-

Step 2. Convert the units you use as needed
Sometimes, you may calculate speed using a certain unit, but need to convert it to another unit. In this case, you need to use a conversion factor to get the answer according to the correct units. To do this, simply write the relationship between the units in the form of a fraction and multiply. When multiplying, reverse the fraction as needed to remove unwanted units. This method is much easier than it sounds!
-
For example, let's say that in the example problem above, we need the answer in miles instead of kilometers. One mile equals about 1.6 kilometers. So, we can do the conversion as follows:
-
- 80 kilometers × 1 mile/1.6 kilometers = 50 miles
-
- Remember, because kilometers appear at the bottom of the fraction, it removes kilometers from the previous answer, so the final result uses miles.
- This website provides conversion features for most of the commonly used units.

Step 3. Replace the "distance" variable with the distance formula as needed
Objects do not always move in a straight and smooth path. If this is true, you may not be able to simply enter a numeric value as a unit of distance into the standard velocity formula. However, you may need to replace the letter j in the formula k = j/w with a formula that resembles the distance traveled by the object.
-
For example, let's say that an airplane rotates through the air a distance of 20 miles 5 times. The plane completed the round in half an hour. In this example, we still need to find the total distance traveled by the plane before we can determine its speed. We can use the formula for calculating the distance around a circle (distance around it) instead of j in this formula. This formula is circumference = 2πr where r = radius of circle. Here's how to solve it:
-
- k = (2 × × r)/w
- k = (2 × × 10)/0.5
- k = 62.83/0.5 = 125.66 miles/hour
-

Step 4. Understand that k = j/w gives the average velocity
The easy and simple formula we use to find velocity has one drawback. The resulting value is technically the average speed. This means that the formula assumes that the object you are measuring uses the same velocity as it moves. As we will see below, finding the velocity of an object in a single moment will be much more difficult.
To illustrate this difference, imagine the last time you traveled by car. It's unlikely that you'll be traveling at the same speed as you're traveling. However, you will usually start your journey at a low speed and gradually increase your speed along the way, stopping due to red lights, traffic jams, etc. If you use the standard speed formula to find speed during travel, changes to that speed cannot be detected. However, you will get an answer that shows the average speed of all the speed differences you travel
Method 3 of 3: Calculating Instant Speed
Note:
This section uses techniques that are less familiar to people who have never studied calculus. Read our articles on calculus for help.
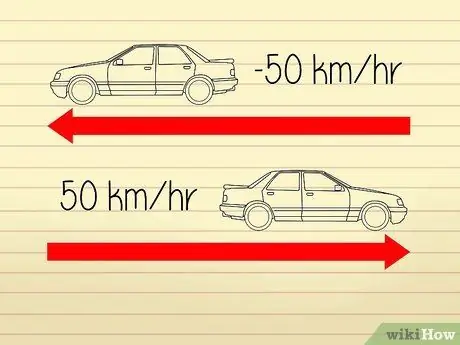
Step 1. Understand that velocity is defined as the rate of acceleration
High-level velocity calculations are quite confusing because mathematicians and scientists use different definitions to describe "speed" and "acceleration". Acceleration has two components: a "rate" and a "direction". The rate is equal to the object's speed. A change in direction will cause a change in acceleration, but not a change in velocity.
- For example, let's say that two cars are moving in opposite directions. The speedometers on both cars display a figure of 50 km/h so they are both traveling at the same speed. However, since the cars are moving away from each other, we can say that one of the cars has an “acceleration” of -50 km/h while the other has an “acceleration” of 50 km/h.
- Just like instantaneous velocity calculations, you can also perform instantaneous acceleration calculations.

Step 2. Use absolute values to measure negative acceleration
An object can have a negative rate of acceleration (if it is moving in a negative direction relative to another object). However, there is no negative speed. So, in this case, the absolute value of the rate indicates the object's velocity.
For this reason, in the example problem above, both cars have a speed of 50km/h.
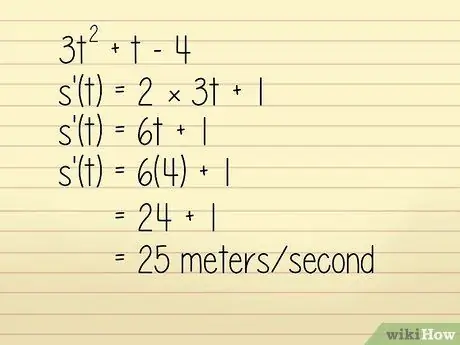
Step 3. Take the derivative of the position of the function
If you have a function k(w) that shows the position of an object without needing to calculate the time, the derivative of k(w) will show the acceleration without the need for timing. Just plug the time value into this formula so that the variable w (or whatever time value is used) gets accelerated according to that time. From here, you can easily find the object's velocity.
-
For example, let's say that the position of an object in one meter is described in the equation 3q2 + w - 4 where w = time in seconds. We want to know the object's velocity at w = 4 seconds. In this case, you can solve it by:
-
- 3w2 +w - 4
- k'(w) = 2 × 3w + 1
- k'(w) = 6w + 1
-
-
Now, we enter w = 4:
-
- k'(w) = 6(4) + 1 = 24 + 1 = 25 meters/second. Technically this is an acceleration calculation, but since it is positive and the direction is not mentioned in the question, we can use it to find the velocity.
-

Step 4. Take the integral acceleration function
Acceleration is a way of measuring the change in the acceleration of an object over time. This topic is too complex to be fully explained in this article. However, it's useful to note that when you have a function a(w) that represents acceleration with respect to time, the integral of a(w) will return the result of acceleration based on that time. Remember, it is very useful to know the initial acceleration of an object so that you can define the constant of that result from an infinite integral.
-
For example, let's say that an object has a constant acceleration (in m/s2 as a result of a(w) = -30. Also say that the object has an initial acceleration of 10 m/s. We need to find the velocity at w = 12 seconds. In this case, we can solve it by:
-
- a(w) = -30
- p(w)= a(w)dw = -30dw = -30w + C
-
-
To find C, we will solve p(w) for w = 0. Remember that the object's initial acceleration is 10 m/s.
-
- p(0) = 10 = -30(0) + C
- 10 = C, so p(w) = -30w + 10
-
-
Now, we can enter w = 12 seconds.
-
- p(12) = -30(12) + 10 = -360 + 10 = -350. Since velocity is an absolute value of acceleration, the object's velocity is 350 meters/second.
-
Tips
- Practice makes great! Try to create your own question by replacing the numbers in the example problem above.
- If you're looking for a quick way to practice calculus for better calculation speed, use the online derivative calculator here and the online integral calculator here.






