- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-06-01 06:05.
A parallel line is two lines in a plane that will never meet (meaning that the two lines will not intersect each other even if they are extended indefinitely). The key feature of parallel lines is that they have exactly the same slope. The slope of a line is defined as the vertical increase (change in the Y coordinate) to the horizontal increase (change in the coordinates of the X axis) of a line, in other words, the slope is the slope of a line. Parallel lines are often represented by two vertical lines (ll). For example, ABCCD shows that the line AB is parallel to CD.
Step
Method 1 of 3: Comparing the Slope of Each Line

Step 1. Determine the slope formula
The slope of a line is defined as (Y2 - Y1)/(X2 - X1), X and Y are the vertical and horizontal coordinates of the points on the line. You have to define two points to calculate with this formula. The point closer to the bottom of the line is (X1, Y1) and the higher point on the line, above the first point, is (X2, Y2).
- This formula can be restated as the vertical increment versus the horizontal increment. Increment is the change in vertical coordinates to changes in horizontal coordinates, or the slope of a line.
- If a line is sloping to the right, the slope is positive.
- If a line slops to the bottom right, the slope is negative.
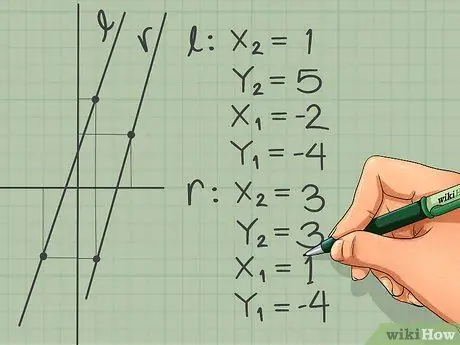
Step 2. Identify the X and Y coordinates of the two points on each line
The point on the line has coordinates (X, Y), X is the position of the point on the horizontal axis and Y is its position on the vertical axis. To calculate slope, you must identify two points on each line whose parallels are identified.
- The points on the line are easy to determine if the line is drawn on graph paper.
- To determine a point, draw a dotted line on the horizontal axis until it intersects the axis of the line. The position where you start to draw a line on the horizontal axis is the X coordinate, while the Y coordinate is where the dotted line intersects the vertical axis.
- For example: line l has points (1, 5) and (-2, 4), while line r has coordinate points (3, 3) and (1, -4).
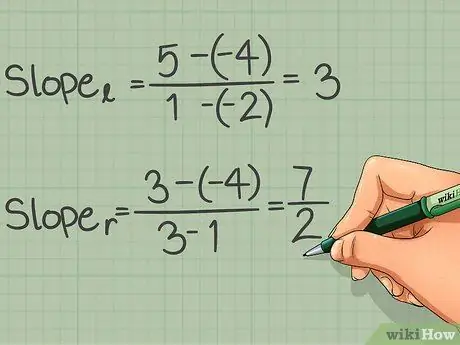
Step 3. Enter the coordinates of each line into the slope formula
To calculate the true slope, simply enter the number, subtract, and then divide. Make sure you enter the appropriate X and Y coordinate values into the formula.
- To calculate the slope of the line l: slope = (5 - (-4))/(1 - (-2))
- Subtract: slope = 9/3
- Divide: slope = 3
- The slope of the line r is: slope = (3 - (-4))/(3 - 1) = 7/2
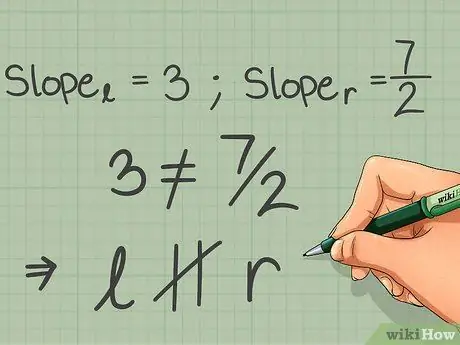
Step 4. Compare the slope of each line
Remember, two lines are only parallel if they have the exact same slope. Lines drawn on paper may appear parallel or very close to parallel, but if the slopes are not exactly the same, the two lines are not parallel.
In this example, 3 is not equal to 7/2, so these two lines are not parallel
Method 2 of 3: Using the Slope Intersection Formula
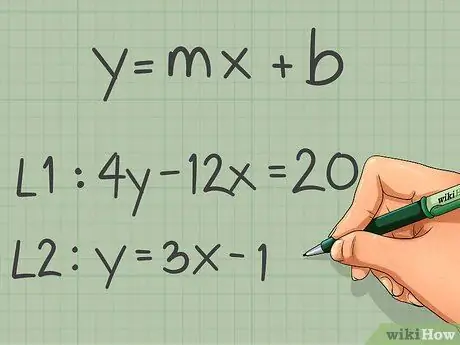
Step 1. Define the formula for the intersection of the slopes of a line
The formula for a line in the form of a slope intersection is y = mx + b, m is the slope, b is the y-intercept, while x and y represent the coordinates of the line. In general, x and y will still be written as x and y in the formula. In this form, you can easily define the slope of the line as the variable "m".
As an example. Rewrite 4y - 12x = 20 and y = 3x -1. The equation 4y - 12x = 20 must be rewritten using algebra, while y = 3x -1 is already in the form of a slope intersection and does not need to be rewritten

Step 2. Rewrite the equation of the line in the form of the intersection of the slopes
Often, you get the equation of a line that doesn't intersect the slope. It only takes a little mathematical knowledge to make the variable fit the shape of the slope intersection.
- For example: Rewrite the line 4y-12x=20 in the form of a slope intersection.
- Add 12x to both sides of the equation: 4y - 12x + 12x = 20 + 12x
- Divide each side by 4 so that y stands alone: 4y/4 = 12x/4 +20/4
- The form of the slope intersection equation: y = 3x + 5.
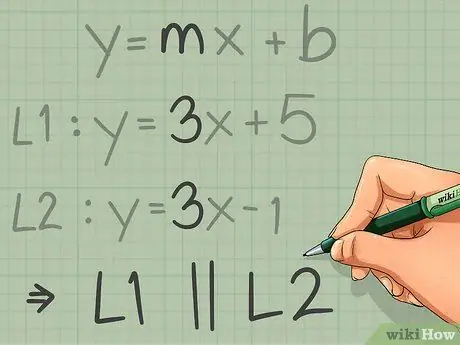
Step 3. Compare the slope of each line
Remember, two parallel lines have exactly the same slope. Using the equation y = mx + b, where m is the slope of the line, you can identify and compare the slopes of the two lines.
- In the example above, the first line has the equation y = 3x + 5, so the slope is 3. The other line has the equation y = 3x - 1, which also has a slope of 3. Since the slopes are identical, the two lines are parallel.
- Notice that both equations have the same y-intercept, they are the same line, not parallel lines.
Method 3 of 3: Defining Parallel Lines with the Equation of Slope of the Point

Step 1. Define the slope equation of the point
The slope form of the point (x, y) allows you to write the equation of a line whose slope is known and has (x, y) coordinates. You will use this formula to define a second parallel to an existing line with a defined slope. The formula is y - y1= m(x - x1), in this case m is the slope of the line, x1 are the coordinates of the point on the line and y1 is the y-coordinate of the point. As in the equation of the slope of the intersection, x and y are variables that indicate the coordinates of the line, in the equation they will still be displayed as x and y.
The following steps can be used with this example: Write the equation of the line parallel to the line y = -4x + 3 through the point (1, -2)

Step 2. Determine the slope of the first line
When writing an equation for a new line, you must first identify the slope of the line that you want to make parallel. Make sure the equation of the starting line is in the form of intersection and slope, meaning that you know the slope (m).
We're going to draw a line parallel to y = -4x + 3. In this equation, -4 represents the variable m, so this is the slope of the line
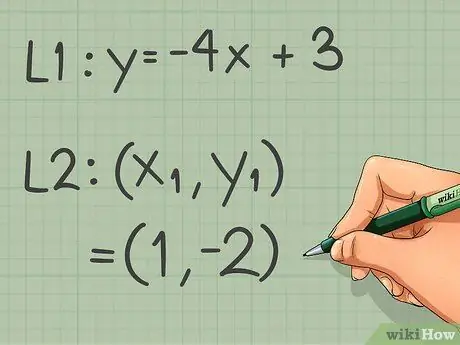
Step 3. Identify a point on the new line
This equation only works if the coordinates passed by the new line are known. Make sure you don't select an existing line coordinate. If the final equations have the same y-intercept, the lines are not parallel, but the same line.
In this example the coordinates of the point are (1, -2)
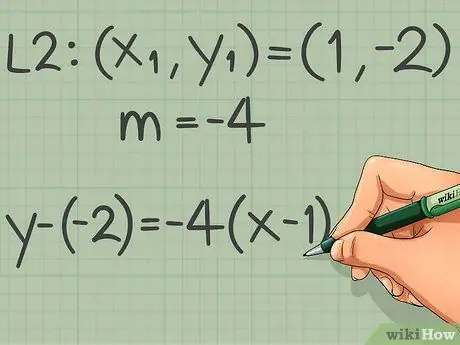
Step 4. Write the equation of the new line in the form of the slope of the point
Remember that the formula is y - y1= m(x - x1). Plug the slope values and point coordinates into the equation of a new line parallel to the first line.
In our example with slope (m) -4 and coordinates (x, y) are (1, -2): y - (-2) = -4(x - 1)
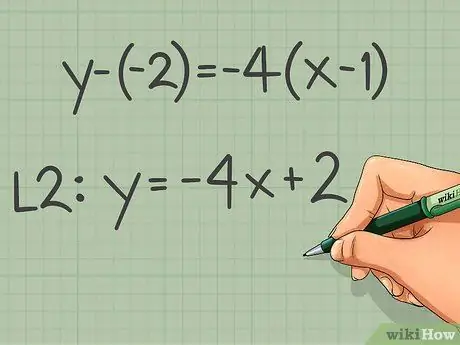
Step 5. Simplify the equation
After plugging in the numbers, the equation can be simplified into the more general form of the slope intersection. If the line of this equation is drawn on the coordinate plane, the line will be parallel to the existing equation.
- For example: y - (-2) = -4(x - 1)
- Two negative signs turn into positive: y + 2 = -4(x -1)
- Distribute -4 to x and -1: y + 2 = -4x + 4.
- Subtract both sides by -2: y + 2 - 2 = -4x + 4 - 2
- Simplified equation: y = -4x + 2






