- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-06-01 06:05.
Simplifying comparisons makes them easier to work with, and the simplification process is quite simple. Find the greatest common factor of both sides of the ratio and divide the entire expression by that quantity.
Step
Method 1 of 3: Method One: Basic Comparison

Step 1. Look at the comparison
Comparison is an expression used to compare two quantities. Simplified comparisons can be done right away, but if the comparison hasn't been simplified, you should simplify it now to make the quantities easier to compare and understand. To simplify the comparison, you must divide both sides by the same number.
-
Example:
15:21
Note that there are no prime numbers in this example. Therefore, you must factor out both numbers to determine if the two terms have the same factor or not, which can be used in the simplification process

Step 2. Factor out the first number
A factor is an integer that divides one term evenly, giving you another whole number. Both terms in the comparison must have at least one factor in common (other than 1). But before you can determine if both terms have the same factors, you'll need to find the factors of each term.
-
Example:
The number 15 has four factors: 1, 3, 5, 15
- 15 / 1 = 15
- 15 / 3 = 5

Step 3. Factor out the second number
In a separate place, list all the factors of the second term of the comparison. For now, don't worry about the factors of the first term and just focus on factoring the second term.
-
Example:
The number 21 has four factors: 1, 3, 7, 21
- 21 / 1 = 21
- 21 / 3 = 7

Step 4. Find the greatest common factor
Look at the factors in the two terms in your comparison. Circle, write a list, or identify all the numbers that appear in both lists. If the equal factor is only 1, then the comparison is in its simplest form and we don't need to do any work. However, if both terms of the comparison have another factor in common, find that factor and identify the largest number. This number is your greatest common factor (GCF).
-
Example:
Both 15 and 21 have two factors in common: 1 and 3
The GCF for both numbers from your initial comparison is 3

Step 5. Divide both sides by their greatest common factor
Since both terms of your original comparison have the same GCF, you can divide the two sides separately and produce a whole number. Both sides must be divided by their GCF; don't just split one side.
-
Example:
Both 15 and 21 must be divided by 3.
- 15 / 3 = 5
- 21 / 3 = 7

Step 6. Write down the final answer
You should have the new terms on both sides of the comparison. Your new ratio is equal to the original ratio, meaning that the quantities of the two forms are in the same proportion. Also note that the quantities on both sides of your new comparison shouldn't have the same factors.
-
Example:
5:7
Method 2 of 3: Method Two: Simple Algebra Comparison

Step 1. Look at the comparison
This type of comparison still compares two quantities, but there is a variable on one or both sides. You must simplify both numeric and variable terms when looking for the simplest form of this comparison.
-
Example:
18x2:72x

Step 2. Factor out both terms
Remember that factors are whole numbers that can evenly divide a given quantity. Look at the numerical values on both sides of the comparison. Write down all the factors of the two terms in a separate list.
-
Example:
To solve this problem, you have to find the factors of 18 and 72.
- The factors of 18 are: 1, 2, 3, 6, 9, 18
- The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72

Step 3. Find the greatest common factor
Look at both lists of factors and circle, underline, or identify all the factors that both lists have in common. From this new selection of numbers, identify the largest number. This value is your greatest common factor (GCF) of the terms. However, note that this value represents only a fraction of your actual GCF in comparison.
-
Example:
Both 18 and 72 have several factors in common: 1, 2, 3, 6, 9, and 18. Of all these factors, 18 is the largest.

Step 4. Divide both sides by their greatest common factor
You should be able to evenly divide both terms in your ratio to the GCF. Do that division now and write down the whole number you came up with. These numbers will be used in your final simplified comparison.
-
Example:
Both 18 and 72 are divisible by a factor of 18.
- 18 / 18 = 1
- 72 / 18 = 4
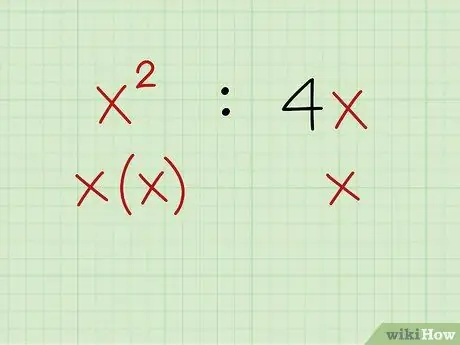
Step 5. Factor out the variables, if possible
Look at the variables on both sides of the comparison. If the same variable appears on both sides of the comparison, then that variable can be factored out.
- Look at the exponents of the variables on both sides. The lower power must be subtracted from the larger power. Understand that by subtracting one power from another, you are essentially dividing the larger variable by the smaller variable.
-
Example:
When examined separately, the variable of the comparison is: x2:x
- You can factor out x from both sides. The power of the first x is 2, and the power of the second x is 1. Thus, one x can be factored out from both sides. The first term will be left with one x and the second term will be left without x.
- x * (x:1)
- x:1
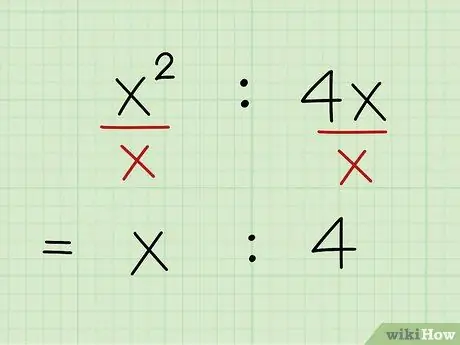
Step 6. Record your true greatest common factor
Combine the GCF of your numeric values with the GCF of your variables to find your true GCF. The GCF is actually the term that must be factored out of all your comparisons.
-
Example:
Your greatest common factor for this problem is 18x.
18x * (x:4)

Step 7. Write down your final answer
After you eliminate your GCF, the remaining comparisons are the simplified form of your original problem. This new comparison should be equal to the original ratio and the terms on both sides of the comparison must not have the same factors.
-
Example:
x:4
Method 3 of 3: Method Three: Polynomial Comparison
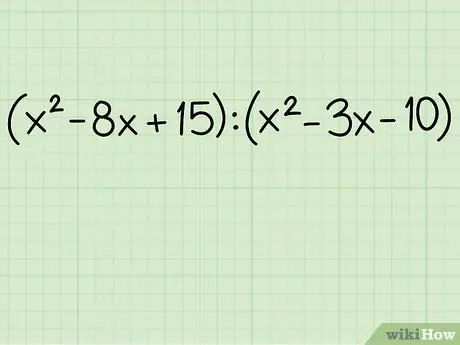
Step 1. Look at the comparison
Polynomial comparisons are more complicated than other types of comparisons. There are still two quantities being compared, but the factors of those quantities are not very visible and the problem may take longer to complete. However, the basic principles and steps remain the same.
-
Example:
(9x2 - 8x + 15): (x2 + 5x - 10)
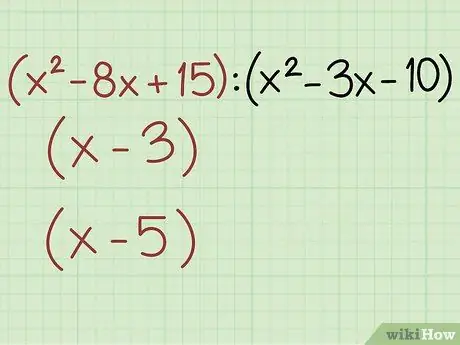
Step 2. Split the first quantity into its factors
You need to factor out the polynomial from the first quantity. There are several ways you can complete this step, so you will need to use your knowledge of quadratic equations and other complex polynomials to determine the best way to use them.
-
Example:
For this problem, you can use the factorization decomposition method.
- x2 - 8x + 15
- Multiply the terms a and c: 1 * 15 = 15
- Find two numbers that are equal to c when multiplied and equal to the value of the term b when added: -5, -3 [-5 * -3 = 15; -5 + -3 = -8]
- Substitute these two numbers into the original equation: x2 - 5x - 3x + 15
- Factor by grouping: (x - 3) * (x - 5)
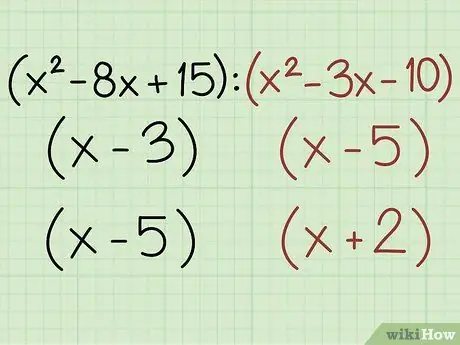
Step 3. Break down the second quantity into its factors
The second quantity of comparison must also be translated into its factors.
-
Example:
Use whatever method you want to break down the second expression into its factors:
-
x2 + 5x - 10
(x - 5) * (x + 2)
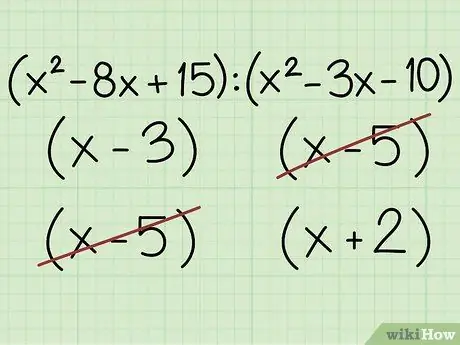
Step 4. Cross out the same factors
Compare the two forms of your initial factored expression. Note that the factor in this implementation is any set of expressions in parentheses. If any of the factors in parentheses on both sides of your comparison are equal, then those factors can be crossed out.
-
Example:
The form of factored comparison is written as: [(x-3)(x-5)]: [(x-5)(x+2)]
- The factors that are common between the numerator and denominator are: (x-5)
- When the same factor is omitted, the ratio can be written as: (x-5)*[(x-3): (x+2)]

Step 5. Write down your final answer
The final comparison must not have additional terms such as factors and must be equal to the initial comparison.
-
Example:
(x - 3): (x + 2)






