How to Find a Line Gradient: 9 Steps (with Pictures)

2024 Author: Jason Gerald | [email protected]. Last modified: 2024-01-19 22:11

Lines can be found anywhere in math, whether you're taking Algebra 1, Geometry, or Algebra 2. If you know how to find the gradient of a line, many things will become clear, for example if the two lines are parallel or perpendicular, intersect, and many other concepts. Finding the gradient of a line is actually very easy. Continue reading for some easy steps you can use to learn how to find line gradients.

Step

Method 1 of 2: Gradient Formula

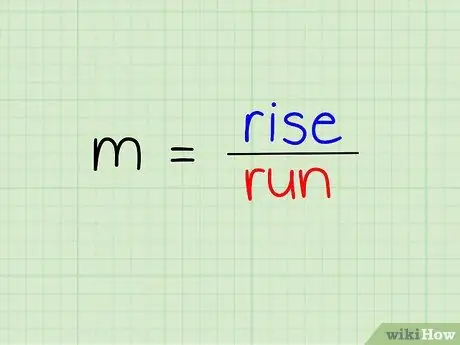
Step 1. Understand the gradient formula

The gradient is defined as vertical divided by horizontal.

Method 2 of 2: Finding the Gradient

Step 1. Find the line you want to find the gradient for

Make sure the line is straight. You can't find the gradient of a line that isn't straight.

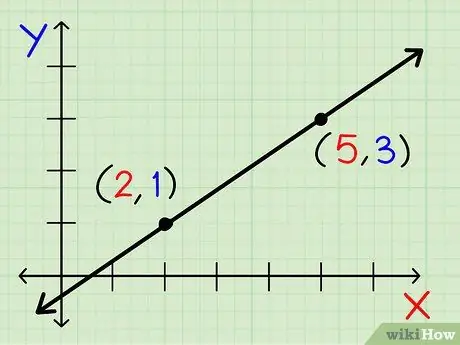
Step 2. Choose any two coordinates that the line passes through

The coordinates are the written x and y points (x, y). It doesn't matter which point you choose, as long as the points are different and lie on the same line.

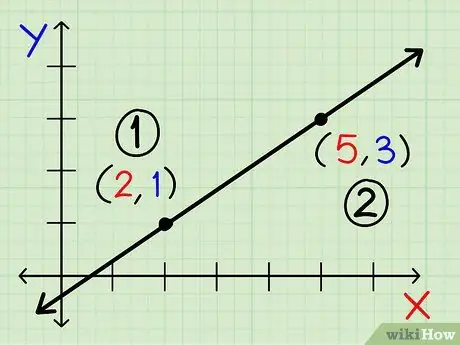
Step 3. Choose the dominant coordinate point in your equation

It doesn't matter which point you choose, as long as the value is always the same during the calculation. The dominant coordinate is x ₁ and y ₁. The other coordinate is x ₂ and y ₂.

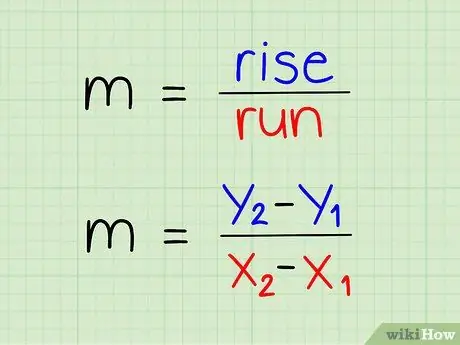
Step 4. Write your equation with the y-coordinate above and the x-coordinate below

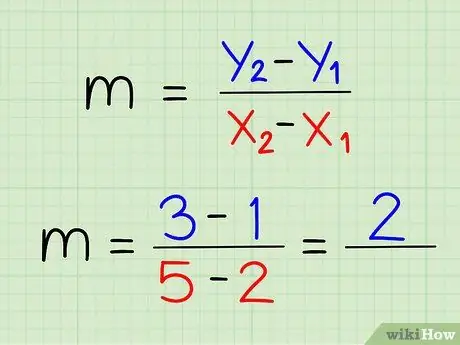
Step 5. Subtract the two y-coordinates from each other

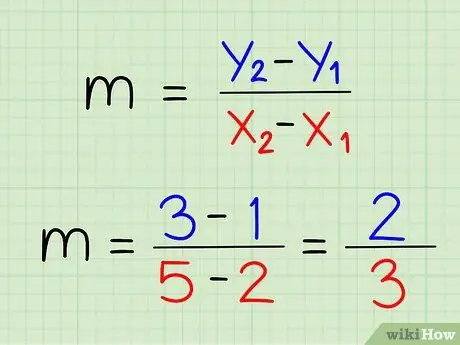
Step 6. Subtract the two x coordinates from each other

Step 7. Divide the result of subtracting the y-coordinate by the result of subtracting the x-coordinate

Simplify the number if it can be simplified.

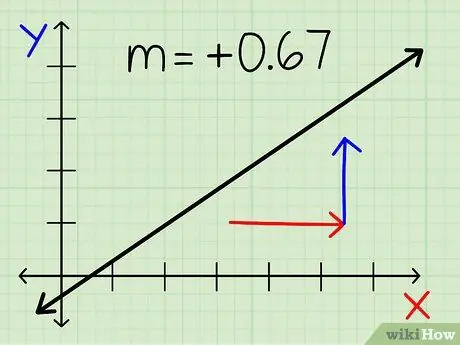
Step 8. Double-check to check if your answer makes sense

• A line that goes from left to right is always positive, even if it is a fraction.
• The line that goes down from left to right is always negative, even if it's a fraction.

Example

1. Known: Line AB.
2. Coordinates: A - (-2, 0) B - (0, -2)
3. (y₂-y₁): -2-0=-2; Vertical = -2
4. (x₂-x₁): 0-(-2)=2; Horizontal = 2

5. Gradient of Line AB = (Vertical/Horizontal) = -1.

   Tips

   • If you have already selected the coordinates of your dominant point, do not swap them for other coordinates or your answer will be wrong.
   • You will find m in the Line Formula, which is: y=mx+b, where y is the y-coordinate of any point, m is the gradient, x is the x-coordinate corresponding to the y-coordinate of any point, and b is the y-intercept.
   • You can also look in your school textbook or ask your teacher.