- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
Mathematics students are often asked to write down their answers in their simplest form - in other words, to write down the answers as elegantly as possible. Although long, stiff and short, as well as elegant, equations are technically the same thing, often, a math problem is not considered complete if the final answer is not reduced to its simplest form. Also, the answer in its simplest form is almost always the easiest equation to work with. For this reason, learning how to simplify equations is an important skill for mathematicians.
Step
Method 1 of 2: Using Operation Sequence

Step 1. Know the order of operations
When simplifying mathematical expressions, you can't just work from left to right, multiplying, adding, subtracting, and so on in order from left to right. Some mathematical operations must take precedence over others and be done first. In fact, using the wrong order of operations can give the wrong answer. The order of operations is: the part in parentheses, the exponent, the multiplication, the division, the addition, and finally, the subtraction. An acronym you can use to remember is Because Mother Is Not Good, Evil, and Poor.
Note that, while a basic knowledge of the order of operations can simplify the most basic equations, special techniques are required to simplify many variable equations, including nearly all polynomials. See the following second method for more information
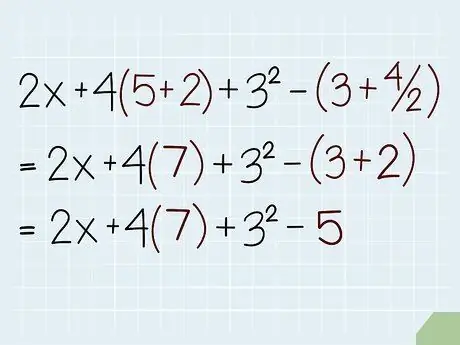
Step 2. Start by completing all the sections in parentheses
In mathematics, parentheses indicate that the inner part must be calculated separately from the expression that is outside the parentheses. Regardless of any operations in parentheses, be sure to complete the part in parentheses first when you're trying to simplify an equation. For example, in parentheses, you must multiply before adding, subtracting, and so on.
-
For example, let's try to simplify the equation 2x + 4(5 + 2) + 32 - (3 + 4/2). In this equation, we have to solve the part inside the brackets, namely 5 + 2 and 3 + 4/2, first. 5 + 2 =
Step 7.. 3 + 4/2 = 3 + 2
Step 5
The part in the second bracket is simplified to 5 because according to the order of operations, we divide 4/2 first in the brackets. If we just work from left to right, we add 3 and 4 first, then divide by 2, giving the wrong answer 7/2
- Note - if there are multiple parentheses in parentheses, complete the section in the innermost bracket, then the second innermost, and so on.
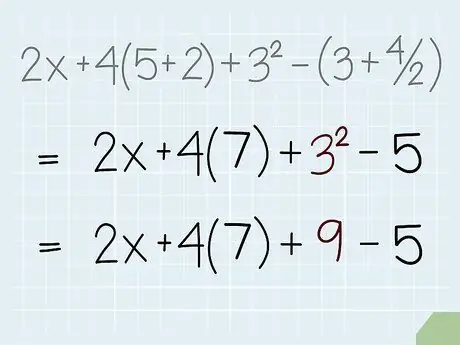
Step 3. Solve the exponent
After completing the brackets, next, solve the exponent of your equation. This is easy to remember because in exponents, the base number and the power to the power are next to each other. Find the answer to each part of the exponent, then plug your answer into the equation to replace the exponent part.
After completing the part in parentheses, our example equation now becomes 2x + 4(7) + 32 - 5. The only exponential in our example is 32, which is equal to 9. Add this result to your equation to replace 32 resulting in 2x + 4(7) + 9 - 5.
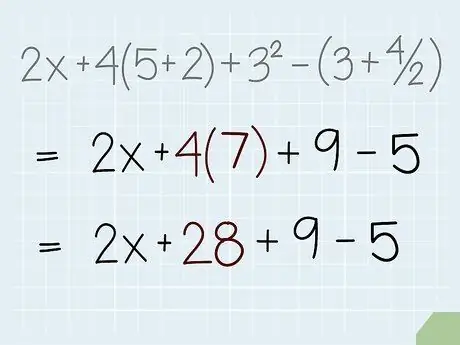
Step 4. Solve the multiplication problem in your equation
Next, do whatever multiplication is needed in your equation. Remember that multiplication can be written in several ways. The × dot, or asterisk symbol is a way of showing multiplication. However, a number next to parentheses or a variable (such as 4(x)) also represents a multiplication.
-
There are two parts to multiplication in our problem: 2x (2x is 2 × x) and 4(7). We don't know the value of x, so we just leave it at 2x. 4(7) = 4 × 7 =
Step 28.. We can rewrite our equation to be 2x + 28 + 9 - 5.
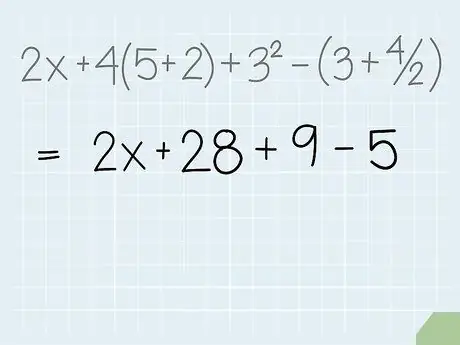
Step 5. Proceed to division
When you're looking for division problems in your equations, keep in mind that, like multiplication, division can be written in a number of ways. One of these is the symbol, but keep in mind that slashes and dashes such as in fractions (eg 3/4) also indicate division.
Because we have already done the division (4/2) when we finished the parts in brackets. Our example doesn't already have a division problem, so we'll skip this step. This shows an important point - you don't have to perform all the operations when simplifying an expression, only the operations contained in your problem
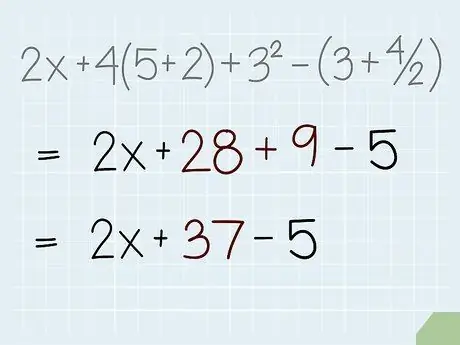
Step 6. Next, add whatever is in your equation
You can work from left to right, but it's easier to add up the easy-to-add numbers first. For example, in the problem 49 + 29 + 51 + 71, it is easier to add 49 + 51 = 100, 29 + 71 = 100, and 100 + 100 = 200, than 49 + 29 = 78, 78 + 51 = 129, and 129 + 71 = 200.
Our example equation has been partially simplified to 2x + 28 + 9 - 5. Now, we have to add up the numbers we can add up - let's look at each addition problem from left to right. We can't add 2x and 28 because we don't know the value of x, so we'll just skip it. 28 + 9 = 37, can be rewritten as 2x + 37 - 5.

Step 7. The last step of the sequence of operations is subtraction
Continue your problem by solving the remaining subtraction problems. You may be able to think of subtraction as adding negative numbers in this step, or using the same steps as for a regular addition problem - your choice will not affect your answer.
-
In our problem, 2x + 37 - 5, there is only one subtraction problem. 37 - 5 =
Step 32.
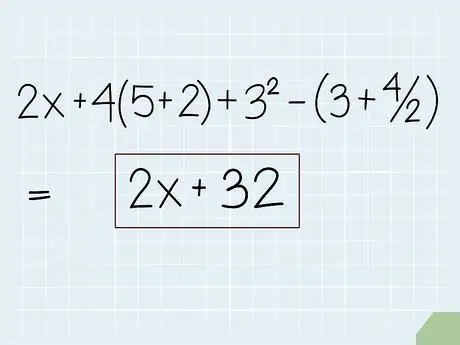
Step 8. Check your equation
After solving using the order of operations, your equation should be simplified to its simplest form. However, if your equation contains one or more variables, understand that your variables do not need to be worked on. To simplify a variable, you must either find the value of your variable or use special techniques to simplify the expression (see step below).
Our final answer is 2x + 32. We can't solve this final addition unless we know the value of x, but if we knew its value, this equation would be much easier to solve than our long original equation
Method 2 of 2: Simplifying Complex Equations
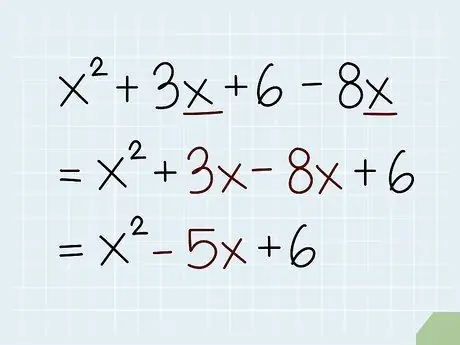
Step 1. Add up the parts that have the same variable
When solving variable equations, keep in mind that parts that have the same variable and exponent (or the same variable) can be added and subtracted like normal numbers. This part must have the same variable and exponent. For example, 7x and 5x can be added, but 7x and 5x2 cannot be added up.
- This rule also applies to some variables. For example, 2xy2 can be summed by -3xy2, but cannot be summed by -3x2y or -3y2.
- See equation x2 + 3x + 6 - 8x. In this equation, we can add 3x and -8x because they have the same variable and exponent. The simple equation becomes x2 - 5x + 6.
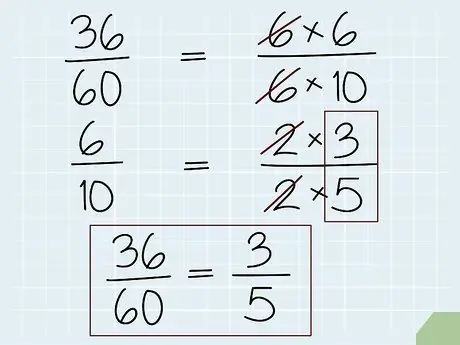
Step 2. Simplify fractional numbers by dividing or crossing out the factors
Fractions that have only numbers (and no variables) in the numerator and denominator can be simplified in several ways. The first, and perhaps the easiest, is to think of the fraction as a division problem and divide the denominator by the numerator. Also, any multiplication factor that appears in the numerator and denominator can be crossed out because dividing the two factors results in the number 1.
For example, look at the fraction 36/60. If we have a calculator, we can divide it to get the answer 0, 6. However, if we don't have a calculator, we can still simplify it by crossing out the same factors. Another way of imagining 36/60 is (6 × 6)/(6 × 10). This fraction can be written as 6/6 × 6/10. 6/6 = 1, so our fraction is actually 1 × 6/10 = 6/10. However, we are not done yet - both 6 and 10 have the same factor, which is 2. Repeating the above method, the result becomes 3/5.
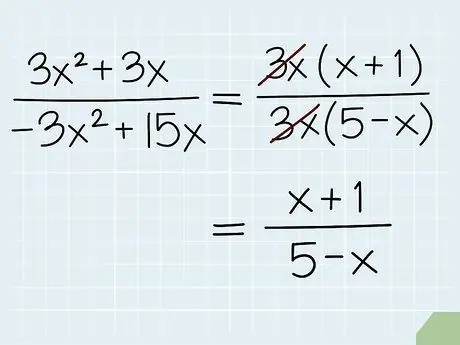
Step 3. On the variable fraction, cross out all the factors of the variable
Variable equations in fraction form have a unique way of simplifying. Like ordinary fractions, variable fractions allow you to eliminate factors that both the numerator and denominator have in common. However, in variable fractions, these factors can be numbers and equations of the actual variable.
- Let the equation (3x2 + 3x)/(-3x2 + 15x). This fraction can be written as (x + 1)(3x)/(3x)(5 - x), 3x appears in both the numerator and denominator. By crossing these factors out of the equation, the result becomes (x + 1)/(5 - x). Same as in expression (2x2 + 4x + 6)/2, since each part is divisible by 2, we can write the equation as (2(x2 + 2x + 3))/2 and then simplify to x2 + 2x + 3.
- Note that you can't cross out all sections - you can only cross out the multiplication factors that appear in the numerator and denominator. For example, in the expression (x(x + 2))/x, x can be crossed out of both the numerator and denominator, so that it becomes (x + 2)/1 = (x + 2). However, (x + 2)/x cannot be crossed out to 2/1 = 2.
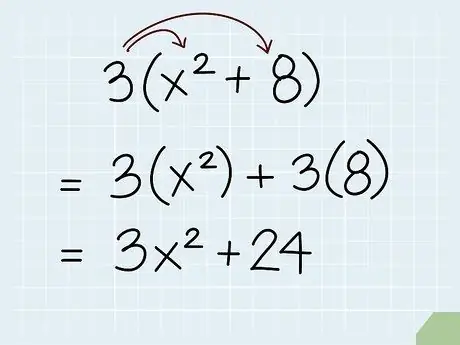
Step 4. Multiply the part in brackets by the constant
When multiplying the part that has the variable in parentheses by a constant, sometimes multiplying each part in the brackets by a constant can result in a simpler equation. This applies to constants that consist only of numbers and constants that have variables.
- For example, equation 3(x2 + 8) can be simplified to 3x2 + 24, whereas 3x(x2 + 8) can be simplified to 3x3 + 24x.
- Note that, in some cases, such as variable fractions, constants around the parentheses can be crossed out so they don't need to be multiplied by the part in the parentheses. In fractions (3(x2 + 8))/3x, for example, the factor 3 appears in both the numerator and denominator, so we can cross it out and simplify the expression to (x2 + 8)/x. This expression is simpler and easier to work with than (3x3 + 24x)/3x, which is the result we will get if we multiply it.
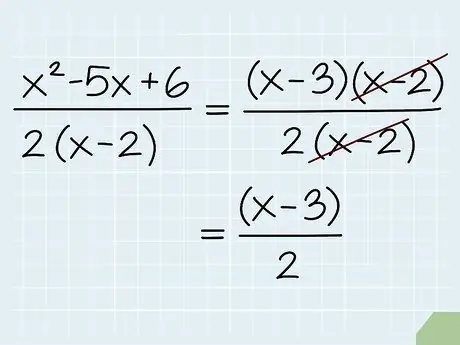
Step 5. Simplify by factoring
Factoring is a technique that can be used to simplify some variable expressions, including polynomials. Think of factoring as the opposite of multiplying by the part in parentheses in the step above - sometimes, an expression can be thought of as two parts being multiplied by each other, rather than a unitary expression. This is especially true if factoring an equation allows you to cross out one of its parts (as in fractions). In certain cases (often with quadratic equations), factoring may even allow you to find the solution to the equation.
- Let us again assume the expression x2 - 5x + 6. This expression can be factored to (x - 3)(x - 2). So, if x2 - 5x + 6 is the numerator of a given equation where the denominator has one of these factors, as in the expression (x2 - 5x + 6)/(2(x - 2)), we might want to write it in factor form so we can cross out the factor with the denominator. In other words, in (x - 3)(x - 2)/(2(x - 2)), the part (x - 2) can be crossed out to be (x - 3)/2.
-
As pointed out above, another reason you might want to factorize your equations is that factoring can give you answers to certain equations, especially if they are written as equals 0. For example, equation x2 - 5x + 6 = 0. Factoring gives (x - 3)(x - 2) = 0. Since any number multiplied by zero equals zero, we know that if any part of the parentheses equals zero, all the equation to the left of the equals sign, is also zero. So that
Step 3. da
Step 2. are the two answers to the equation.






