Determining whether three side lengths can form a triangle is easier than it seems. All you have to do is use the Triangle Inequality Theorem, which states that the sum of the two side lengths of a triangle is always greater than the third side. If this is true for the three combinations of side lengths added together, then you have a triangle.
Step
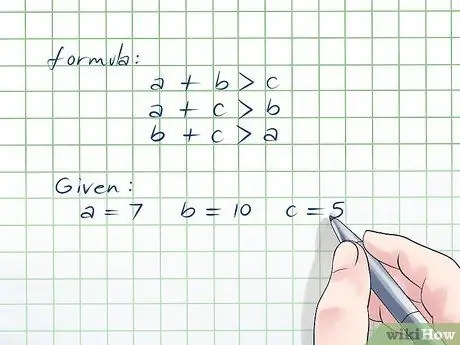
Step 1. Learn the Triangle Inequality Theorem
This theorem simply states that the sum of the two sides of a triangle must be greater than the third side. If this statement is true for all three combinations, then you have a valid triangle. You'll need to calculate these combinations one by one to make sure that the triangle is usable. You can also imagine a triangle having side lengths a, b, and c, and think of the theorem as an inequality, which states: a+b > c, a+c > b, and b+c > a.
For this example, a = 7, b = 10, and c = 5
Step 2. Check to see if the sum of the first two sides is greater than the third side
In this problem, you can add sides a and b, or 7 + 10, to get 17 which is greater than 5. You can also think of it as 17 > 5.
Step 3. Check to see if the sum of the next two-sided combinations is greater than the remaining sides
Now, see if the sum of sides a and c is greater than side b. This means that you have to see if 7 + 5, or 12 is greater than 10. 12 > 10, so it is greater.
Step 4. Check to see if the sum of the last two side combinations is greater than the remaining sides
You need to see if the sum of side b and side c is greater than side a. To do this, you have to see if 10 + 5 is greater than 7. 10 + 5 = 15, and 15 > 7, so these three sides pass the test and can form a triangle.
Step 5. Check your work
Now that you have checked the side combinations one by one, you can double-check if this rule is true for all three combinations. If the sum of any two side lengths is greater than the third in all combinations, as is the case in this triangle, then you have determined that this triangle is valid. If the rules don't match, even for a single combination, then the triangle is invalid. Since the following statements are true, you have found a valid triangle:
- a + b > c = 17 > 5
- a + c > b = 12 > 10
- b + c > a = 15 > 7
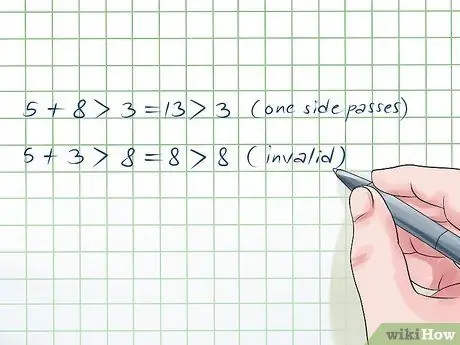
Step 6. Know how to spot invalid triangles
Just for practice, you should make sure that you can figure out the unusable triangles. Suppose you are working with these three side lengths: 5, 8, and 3. Let's see if these sides pass the test:
- 5 + 8 > 3 = 13 > 3, so one side passes the test.
- 5 + 3 > 8 = 8 > 8. Since this calculation is invalid, you can stop here. This shape is not a triangle.
