The asymptote of a polynomial is any straight line that approaches a graph but never touches it. The asymptote can be vertical or horizontal, or it can be an oblique asymptote – an asymptote with a curve. The skewed asymptote of a polynomial is found when the degree of the numerator is higher than the degree of the denominator.
Step
Step 1. Check the numerator and denominator of your polynomial
Make sure that the degree of the numerator (in other words, the highest exponent in the numerator) is greater than the degree of the denominator. If it is greater, then there is an oblique asymptote and the asymptote can be searched.
For example, look at the polynomial x ^2 + 5 x + 2 / x + 3. The degree of the numerator is greater than the degree of the denominator because the numerator has the power of 2 (x ^2) while the denominator only has the power of 1.. The graph of this polynomial is shown in Fig
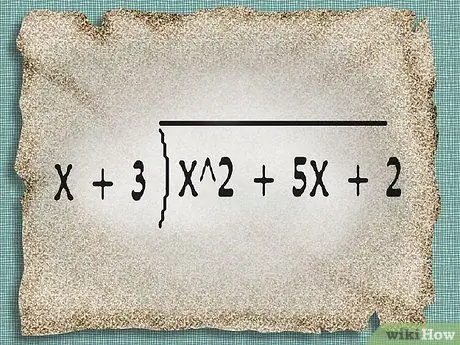
Step 2. Write a long division problem
Put the numerator (which divides) inside the division box, and put the denominator (which divides) outside.
For the example above, set up a long division problem with x ^2 + 5 x + 2 as the dividing expression and x + 3 as the divisor expression
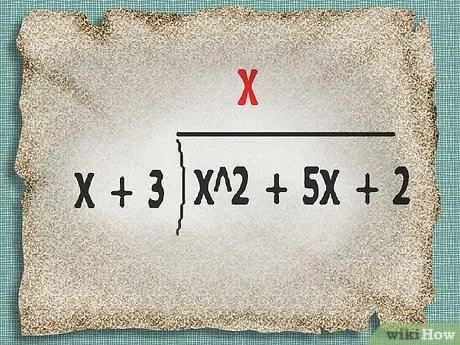
Step 3. Find the first factor
Find a factor that, when multiplied by the term with the highest order in the denominator, will produce the same term as the term with the highest order in the divided expression. Write the factor above the division box.
In the example above, you'll be looking for a factor that, when multiplied by x, will produce the same term as the highest degree x ^2. In this case, the factor is x. Write x above the division box
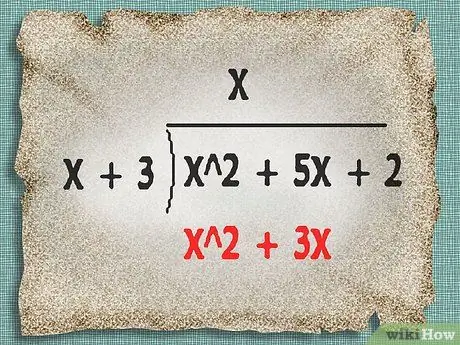
Step 4. Find the product of the factor by all the divisor expressions
Multiply to get your product, and write the result under the divided expression.
In the example above, the product of x and x + 3 is x ^2 + 3 x. Write the result under the divided expression, as shown
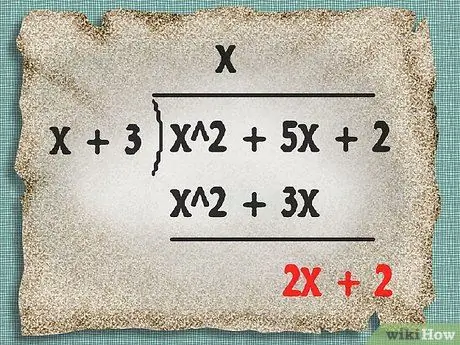
Step 5. Subtract
Take the lower expression below the division box and subtract it from the upper expression. Draw a line and write your subtraction result below it.
In the example above, subtract x ^2 + 3 x from x ^2 + 5 x + 2. Draw a line and write the result, 2 x + 2, below the line, as shown
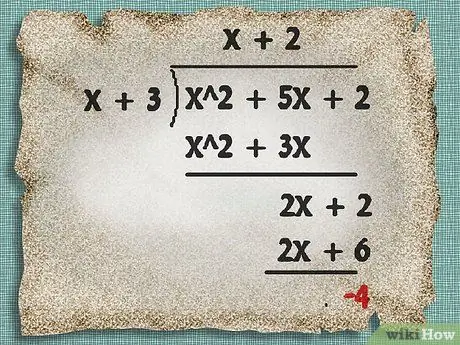
Step 6. Continue dividing
Repeat these steps, using the result of your subtraction problem as the divided expression.
In the example above, note that, if you multiply 2 by the highest term in the divisor (x), you get the term with the highest degree of order in the divided expression, which is now 2 x + 2. Write 2 above the division box by adding it to the factor first, make it x + 2. Write the product of the factor and its divisor under the divided expression, and then subtract it again, as shown
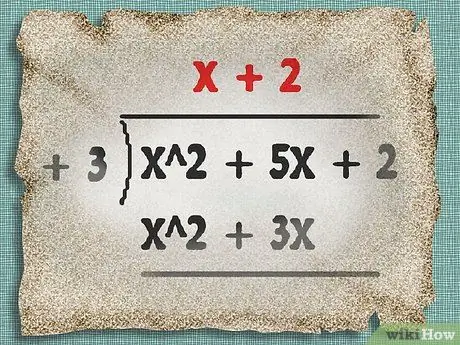
Step 7. Stop when you get the equation of the line
You don't have to do long division until the end. Just continue until you get the equation of the line in the form ax + b, where a and b are any number.
In the example above, you can stop now. The equation of your line is x + 2
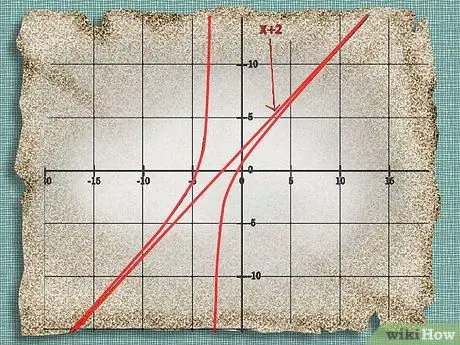
Step 8. Draw a line along the graph of the polynomial
Draw your line graph to make sure that the line is really an asymptote.
In the example above, you would have to draw the graph of x + 2 to see if the line extends along the graph of your polynomial but never touches it, as seen below. So, x + 2 really is an oblique asymptote of your polynomial
Tips
- The lengths of your x-axis should be close together, so you can clearly see that the asymptotes don't touch your polynomial.
- In mechanical engineering, asymptotes are very helpful because asymptotes form estimates of linear behavior that are easy to analyze, for nonlinear behavior.
