- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
While it's easy to sort whole numbers like 1, 3, and 8 by value, at first glance, fractions can be difficult to sort. If each of the bottom numbers, or denominators, are the same, you can sort them like whole numbers, such as 1/5, 3/5, and 8/5. Otherwise, you'll need to change your fractions so they have the same denominator, without changing the value. This gets easier with a lot of practice, and you can also learn some tricks when comparing just two fractions, or when ordering fractions with a larger numerator like 7/3.
Step
Method 1 of 3: Sort All Fractions

Step 1. Find a common denominator for all fractions
Use one of these methods to find the denominator, or number at the bottom of a fraction, that you can use to convert all fractions, so you can easily compare them. This number is called the common denominator, or the least common denominator if it is the smallest possible number:
-
Multiply each different denominator. For example, if you compare 2/3, 5/6, and 1/3, multiply two different denominators: 3 x 6 =
Step 18.. This is a simple method, but often results in larger numbers than the other methods, making it difficult to solve.
-
Or list the multiples of each denominator in a different column, until you find the same number that appears in each column. Use this number. For example, comparing 2/3, 5/6, and 1/3, list the multiples of 3: 3, 6, 9, 12, 15, 18. Then the multiples of 6: 6, 12, 18. Because
Step 18. appears in both lists, use the number. (You can also use 12, but this method will use 18).

Step 2. Change each fraction so that it has the same denominator
Remember, if you multiply the top and bottom of a fraction by the same number, the value of the fraction will remain the same. Use this technique on each fraction individually so that each fraction has the same denominator. Try for 2/3, 5/6, and 1/3, using the same denominator, 18:
- 18 3 = 6, so 2/3 = (2x6)/(3x6)=12/18
- 18 6 = 3, so 5/6 = (5x3)/(6x3)=15/18
- 18 3 = 6, so 1/3 = (1x6)/(3x6)=6/18
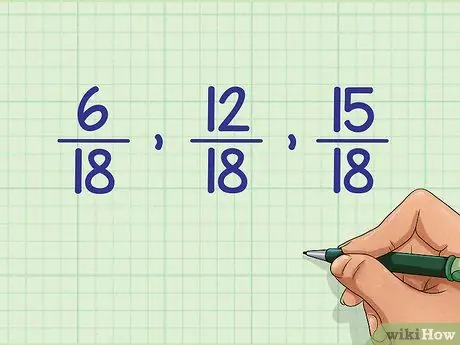
Step 3. Use the top number to sort the fractions
Since all fractions already have the same denominator, it's easy to compare them. Use the top number or the numerator to sort from smallest to largest. Ordering the fractions we found above, we get: 6/18, 12/18, 15/18.

Step 4. Return each fraction to its original shape
Just leave the order of the fractions, but return them to their original form. You can do this by remembering the fraction change, or by dividing the top and bottom of the fraction again:
- 6/18 = (6 ÷ 6)/(18 ÷ 6) = 1/3
- 12/18 = (12 ÷ 6)/(18 ÷ 6) = 2/3
- 15/18 = (15 ÷ 3)/(18 ÷ 3) = 5/6
- The answer is "1/3, 2/3, 5/6"
Method 2 of 3: Sorting Two Fractions Using Cross Product
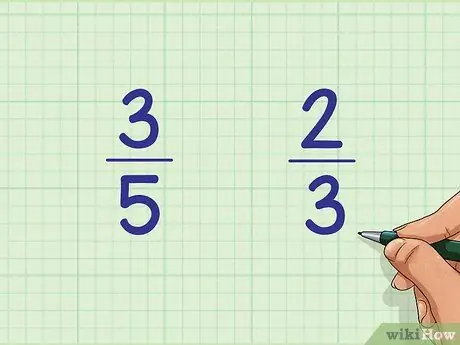
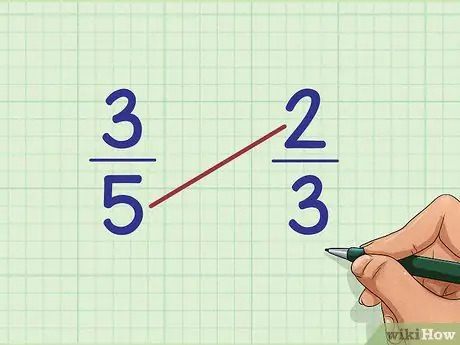
Step 1. Write down the two fractions next to each other
For example, compare the fractions 3/5 and 2/3. Write them next to each other: 3/5 on the left and 2/3 on the right.
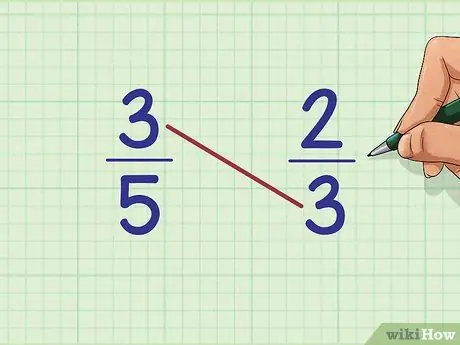
Step 2. Multiply the top number of the first fraction by the bottom number of the second fraction
In our example, the top number or numerator of the first fraction (3/5) is
Step 3.. The bottom number or denominator of the second fraction (2/3) is also
Step 3.. Multiply both: 3 x 3 = ?
This method is called cross product because you are multiplying numbers diagonally with each other
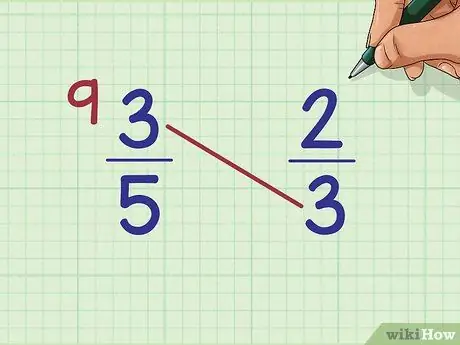
Step 3. Write your answer next to the first fraction
Write your product next to the first fraction on the same page. For example, 3 x 3 = 9, you would write
Step 9. next to the first shard, on the left side of the page.
Step 4. Multiply the top number of the second fraction by the bottom number of the first fraction
To find the larger fraction, we have to compare the answer above with this multiplication answer. Multiply both. For example, for our example (comparing 3/5 and 2/3), multiply 2 x 5.

Step 5. Write the answer next to the second fraction
Write the answer of this second product next to the second fraction. In this example, the result is 10.
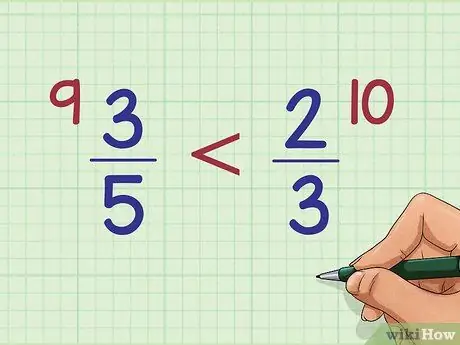
Step 6. Compare the results of the cross product of the two
The answer to this multiplication is called the cross product. If one cross product is greater than the other, then the fraction next to that result is greater than the other fraction. In our example, since 9 is less than 10, it means 3/5 is less than 2/3.
Remember to always write the result of the cross product next to the fraction whose numerator you are using

Step 7. Understand how it works
To compare two fractions, basically, you change the fractions so that they have the same denominator or bottom of the fraction. This is what cross multiplication does! Cross multiplication simply skips the step of writing the denominator. Since both fractions will have the same denominator, you only need to compare the two upper numbers. Here's our example (3/5 vs 2/3), written without the cross multiplication shorthand:
- 3/5=(3x3)/(5x3)=9/15
- 2/3=(2x5)/(3x5)=10/15
- 9/15 is smaller than 10/15
- So, 3/5 is less than 2/3
Method 3 of 3: Sorting Fractions Greater Than One
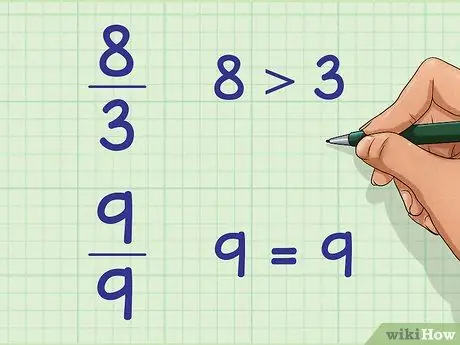
Step 1. Use this method for fractions with a numerator that is equal to or greater than the denominator
If a fraction has an upper number or numerator that is greater than the lower number or denominator, the value is greater than 1. An example of this fraction is 8/3. You can also use this method for fractions with the same numerator and denominator, such as 9/9. These two fractions are examples of unusual fractions.
You can still use other methods for this fraction. This helps fractions look more reasonable, and faster
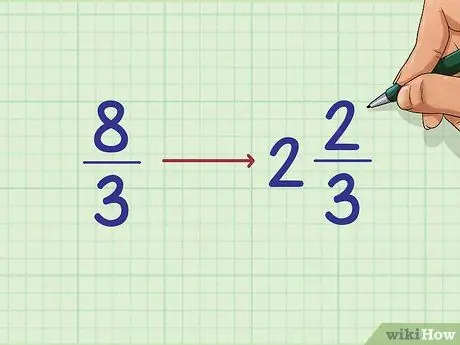
Step 2. Convert every common fraction to a mixed number
Convert it to a mixture of whole numbers and fractions. Sometimes, you can picture it in your head. For example, 9/9 = 1. Other times, use long division to determine how many times the numerator is divisible by the denominator. If there is a remainder from the long division, the number is a fraction remainder. For example:
- 8/3 = 2 + 2/3
- 9/9 = 1
- 19/4 = 4 + 3/4
- 13/6 = 2 + 1/6
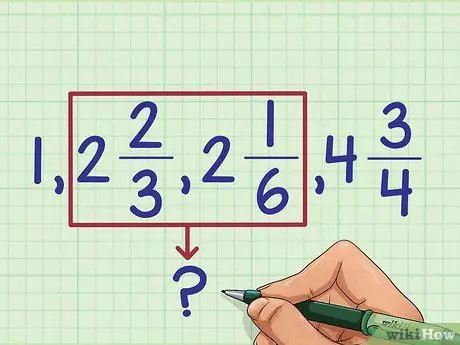
Step 3. Sort the whole numbers
Now that the mixed number has been changed, you can determine the larger number. For now, ignore the fractions, and sort the fractions by the size of the whole number:
- 1 is the smallest
- 2 + 2/3 and 2 + 1/6 (we don't know which fraction is bigger yet)
- 4 + 3/4 is the largest

Step 4. If necessary, compare the fractions from each group
If you have multiple mixed numbers with the same whole number, for example 2 + 2/3 and 2 + 1/6, compare the fractional parts to find the larger fraction. You can use any method in the other sections to do this. Here's an example of comparing 2 + 2/3 and 2 + 1/6, making the denominators of both fractions the same:
- 2/3 = (2x2)/(3x2) = 4/6
- 1/6 = 1/6
- 4/6 is bigger than 1/6
- 2 + 4/6 is greater than 2 + 1/6
- 2 + 2/3 is greater than 2 + 1/6
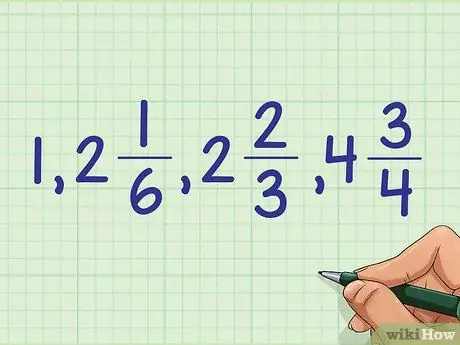
Step 5. Use the result to sort all mixed numbers
Once you've sorted the fractions in each of their mixed number sets, you can sort all your numbers: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.
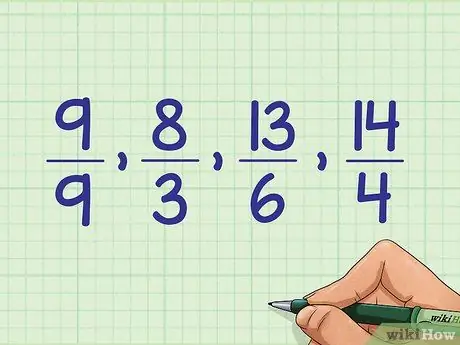
Step 6. Convert the mixed number to its initial fraction form
Leave the sequence the same, but change it to its initial form and write the number as a common fraction: 9/9, 8/3, 13/6, 19/4.
Tips
- If the numerators are all the same, you can order the denominators in reverse order. For example, 1/8 < 1/7 < 1/6 < 1/5. Think of it like pizza: if you initially have 1/2 then it becomes 1/8, you divide the pizza into 8 pieces instead of 2, and every 1 slice you get less.
- When sorting fractions with large numbers, comparing and sorting a small group of numbers consisting of 2, 3, or 4 fractional numbers may be helpful.
- While finding the least common denominator can help you solve problems with smaller numbers, you can actually use any common denominator. Try sorting 2/3, 5/6, and 1/3 using the denominator 36, and see if the answers are the same.






