The area equation for an ellipse will look easy if you've studied circles before. The main point to remember is that an ellipse has two important lengths to measure, namely the major and minor radii.
Step
Part 1 of 2: Calculating Area
Step 1. Find the major radius of the ellipse
This radius is the distance from the center of the ellipse to the farthest end of the ellipse. Think of these radii as the “bulging” radii of the ellipse. Measure the radius or look for the radius indicated on your diagram. We will refer to these fingers as a.
You can call it the semimajor axis
Step 2. Find the minor radius
As you may have guessed, the minor radius measures the distance from the center of the ellipse to the nearest point at the end of the ellipse. Call these fingers b.
- This radius has a right angle of 90 degrees with the major radius. However, you don't need to measure every angle to solve this problem.
- You can call it the semiminor axis.
Step 3. Multiply by pi
The area of the ellipse is a x b x. Since you are multiplying two units of length, your answer is written in units of squares.
- For example, if an ellipse has a major radius of 3 units and a minor radius of 5 units, the area of the ellipse is 3 x 5 x or about 47 squared units.
- If you don't have a calculator or if your calculator doesn't have the symbol, just use 3, 14.
Part 2 of 2: Understanding How It Works
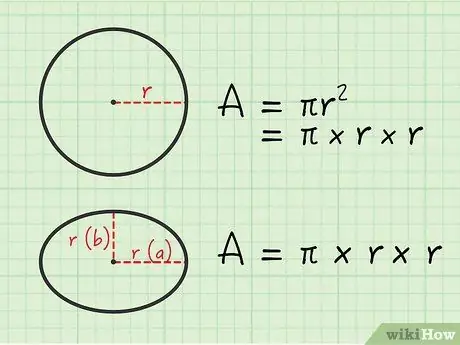
Step 1. Think of the area of a circle
You may remember that the area of a circle is equal to r2, which is equal to x r x r. What if we try to find the area of a circle as if it were an ellipse? We will measure the radius in either direction: r. Measure the radius that is at the right angle: also r. Plug that value into the formula for the ellipse equation: x r x r! As it turns out, circles are just a certain type of ellipse.
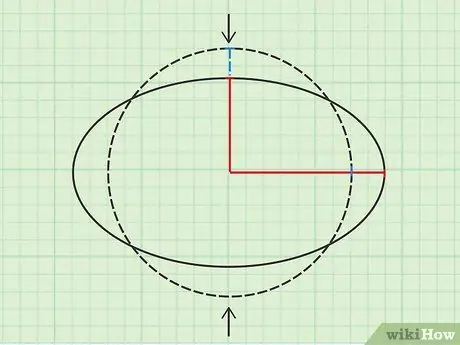
Step 2. Imagine a pressed circle
Imagine a circle pressed so that it forms an ellipse. As the circle is pressed more and more, one of the radii becomes shorter and the other radii become longer. The area remains the same because nothing leaves the circle. As long as we use both radii in our equation, the emphasis and alignment will cancel each other out, and we'll still get the right answer.
