A trapezoid is a four-sided two-dimensional shape with parallel sides and different lengths. The formula for calculating the area of a trapezoid is L = (b1+b2)t, i.e. b1 and b2 is the length of the parallel sides and t is the height. If you only know the side lengths of a regular trapezoid, you can break the trapezoid into simple shapes and find the height and complete the calculation. When you're done, just add units based on the unit length of the sides of the trapezoid!
Step
Method 1 of 2: Finding Area Using Parallel Side Lengths and Height
Step 1. Add up the lengths of the parallel sides
As the name implies, parallel sides are 2 sides of a trapezoid that are parallel to each other. If you don't know the lengths of these two parallel sides, use a ruler to measure them. After that, add up the two.
For example, if you know that the value of the upper parallel side (b1) is 8 cm and the lower parallel side (b2) is 13 cm, the total length of the parallel sides is 8 cm + 13 cm = 21 cm (which reflects the part "b = b1 + b2" in the formula).
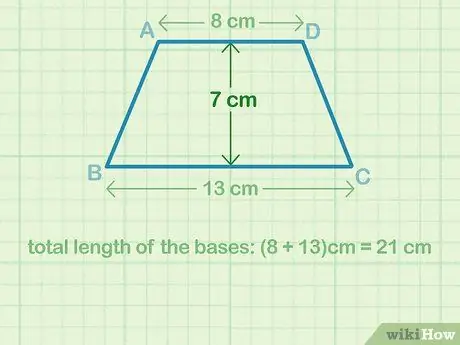
Step 2. Measure the height of the trapezoid
The height of the trapezoid is the distance between the two parallel sides. Draw a line between the two parallel sides and use a ruler or other measuring device to find the length of the line. Take notes so you don't forget or lose them.
The length of the hypotenuse, or the leg of the trapezoid, is not the height of the trapezoid. The height line must be perpendicular to the two parallel sides
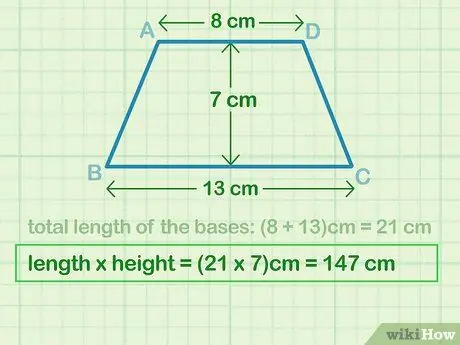
Step 3. Multiply the total of the parallel sides by the height
Next, you need to multiply the number of parallel sides (b) and height (t) of the trapezoid. The answer must have units of square units.
In this example, 21 cm x 7 cm = 147 cm2 which reflects the "(b)t" part of the equation.
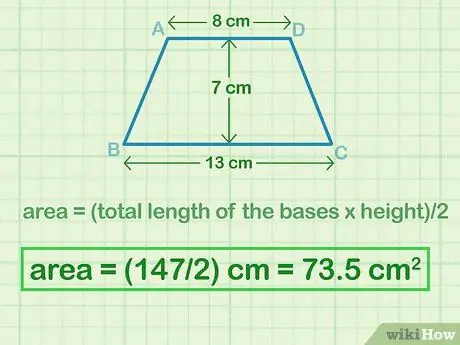
Step 4. Multiply the result by to find the area of the trapezoid
You can multiply the product above by 1/2, or divide by 2 to find the final area of the trapezoid. Make sure the answer unit is in square units.
For this example, the area (L) of the trapezoid is 147 cm2 / 2 = 73.5 cm2.
Method 2 of 2: Calculating the Area of a Trapezoid If You Know the Size of the Sides
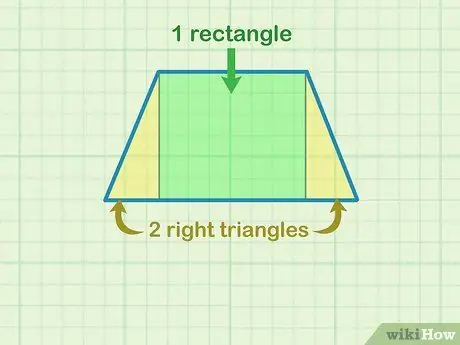
Step 1. Break the trapezoid into 1 rectangle and 2 right triangles
Draw a straight line from each corner of the top side of the trapezoid perpendicular to the bottom side. Now, the trapezoid appears to have 1 rectangle in the middle and 2 right and left triangles. It's a good idea to draw this line so you can see the shape more clearly and calculate the height of the trapezoid.
This method can only be applied to a standard isosceles trapezoid
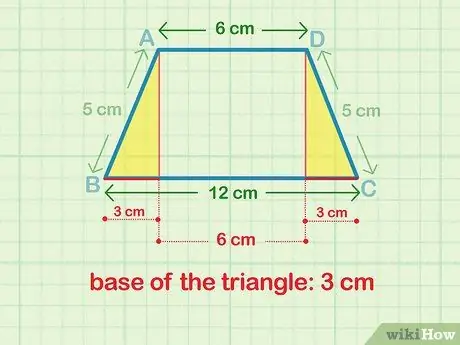
Step 2. Find the length of one of the bases of the triangle
Subtract the bottom side of the trapezoid from the top side. Divide the result by 2 to find the length of the base of the triangle. Now you have the length of the base and hypotenuse of the triangle.
For example, if the upside (b1) is 6 cm long and the bottom side is (b2) 12 cm, meaning that the base of the triangle is 3 cm (because b = (b2 - b1)/2 and (12 cm - 6 cm)/2 = 6 cm which can be simplified to 6 cm/2 = 3 cm).
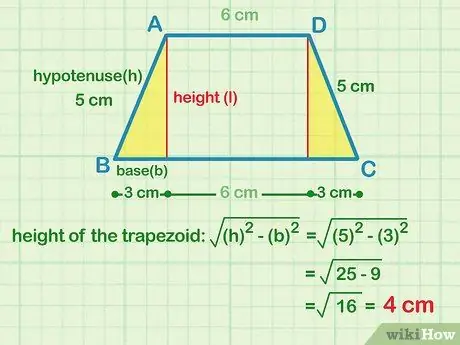
Step 3. Use the Pythagorean theory to find the height of the trapezoid
Plug the lengths of the base and hypotenuse (longest side of the triangle) into the Pythagorean formula A2 + B2 = C2, i.e. A is the base, and C is the hypotenuse. Solve equation B to find the height of the trapezoid. If the length of the side of the base is 3 cm, and the length of the hypotenuse is 5 cm, the following is the calculation:
- Enter variable: (3 cm)2 + B2 = (5 cm)2
- Square the number: 9 cm +B2 = 25 cm
- Subtract each side by 9 cm: B2 = 16 cm
- Find the square root of each side: B = 4 cm
Tips:
If you don't have a perfect square in the equation, simply simplify it as much as possible and leave the remainder as the square root, for example 32 = (16)(2) = 4√2.
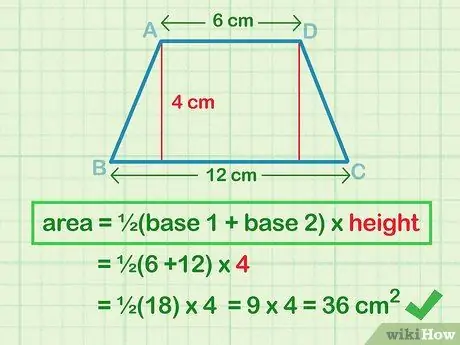
Step 4. Plug the lengths of the parallel sides and the height of the trapezoid into the area formula and solve
Put the base length and height into the formula L = (b1 +b2)t to find the area of the trapezoid. Simplify the numbers as much as possible and give the units squared.
- Write the formula: L = (b1+b2)t
- Enter the variable: L = (6 cm +12 cm)(4 cm)
- Simplify terms: L = (18 cm)(4 cm)
- Multiply the numbers: L = 36 cm2.
