- Author Jason Gerald [email protected].
- Public 2024-01-16 19:04.
- Last modified 2025-06-01 06:05.
So you are given an assignment that requires you to find the area of a quadrilateral… but you don't even know what a quadrilateral is. Don't worry, here's the explanation! A quadrilateral is any shape that has four sides - a square, a rectangle, and a rhombus, for example. To find the area of a rectangle, all you have to do is identify the type of rectangle you're working with and follow a simple formula. Only that!
Step
Method 1 of 4: Squares, Rectangles and Other Parallelograms
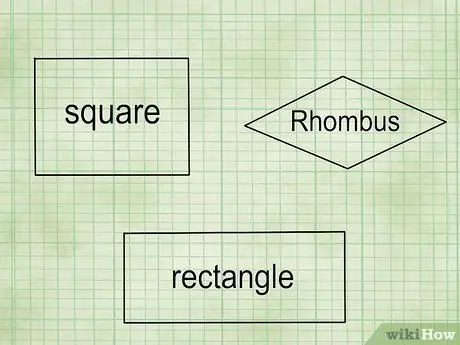
Step 1. Know how to identify a parallelogram
A parallelogram is any quadrilateral with 2 pairs of parallel sides whose opposite or opposite sides are the same length. The parallelogram includes:
-
Rectangle:
Four sides, all the same length. Four angles, all 90 degrees (right angles).
-
Rectangle:
Four sides, the opposite or opposite sides have the same length. Four corners, all 90 degrees.
-
Cut the rice cake:
Four sides, the opposite or opposite sides have the same length. four corners; It doesn't have to be 90 degrees, but opposite angles must have the same angle.
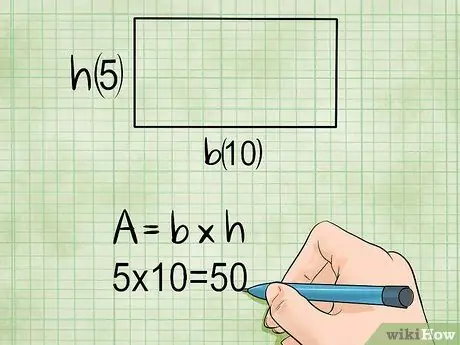
Step 2. Multiply the base by its height to get the area of the rectangle
To find the area of a rectangle, you need two measurements: the length or base (the longer side of the rectangle), and the width or height (the shorter side of the rectangle). Then, just multiply the two to get the area. In other words:
- Area = base × height, or L = a × t in short.
-
Example:
If the base of a rectangle is 10 cm long and 5 cm high, the area of the rectangle is only 10 × 5 (a × h) = 50 cm squared.
- Don't forget that when you find the area of a figure, you will use the units squared (cm squared, m squared, km squared, etc.) for the answer.
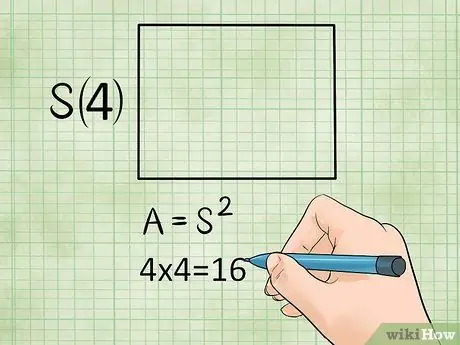
Step 3. Multiply one of the sides by itself to find the area of a square
A square is basically a special rectangle, so you can use the same formula to find its area. However, since the sides of the rectangle are the same length, you can use a quick method of simply multiplying one of the side lengths of the square by itself. This is the same as multiplying the base of a square by its height because the base and height are always the same. Use the following equation:
- Area = side × side or L = s2
-
Example:
If one side of the square has a length of 4 m (s = 4), the area of this square is simply s2, or 4 x 4 = 16 square meters.
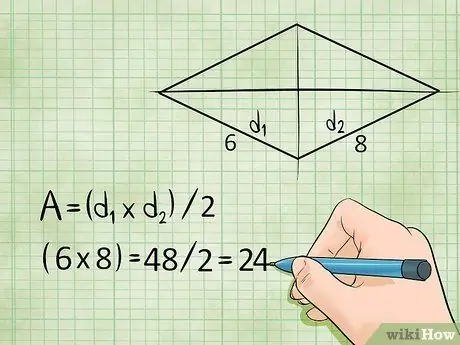
Step 4. Multiply the diagonals and divide by two to find the area of a rhombus
Be careful with rhombuses - when you find the area of a rhombus, you can't just multiply two adjacent sides. Instead, find the diagonals (lines connecting each of the opposite corner points), multiply the diagonals, and divide by two. In other words:
- Area = (Diag. 1 × Diag. 2)/2 or L = (d1 × d2)/2
-
Example:
If a rhombus has diagonals that are 6 meters long and 8 meters long, its area is only (6 × 8)/2 = 48/2 = 24 meters squared.

Step 5. Alternatively, use base × height to find the area of a rhombus
Technically, you can also use the base times height formula to find the area of a rhombus. However, here, "base" and "height" do not mean that you can multiply two adjacent sides. First, select one of the sides to be the base. Then, draw a line from the base to the opposite side. The line hits both sides at a 90 degree angle. This side length is the length you should use as the height.
-
Example:
A rhombus has sides 10 m and 5 m. The straight line distance between the two sides of 10 m is 3 m. If you wanted to find the area of the rhombus, you would multiply 10 × 3 = 30 square meters.
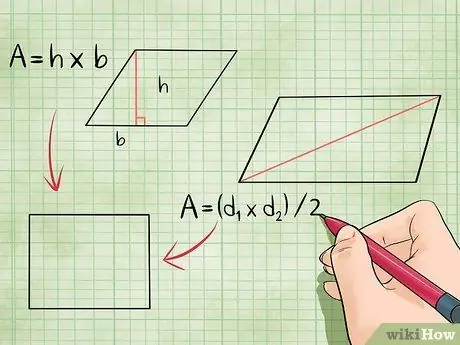
Step 6. Notice that the rhombus and rectangle formulas also apply to squares
The side × side formula given above for a square is by far the easiest way to find the area of this figure. However, since a square is technically a rectangle, a rhombus, and a square, you can use these formulas to find the area of a square and get the correct answer. In other words, for a square:
- Area = base × height or L = a × t
- Area = (Diag. 1 × Diag. 2)/2 or L = (d1 × d2)/2
-
Example:
A figure with four sides, has two adjacent sides with a length of 4 meters. You can find the area of this square by multiplying the base by the height: 4 × 4= 16 square meters.
-
Example:
The two diagonals of a square are 10 cm long. You can find the area of this square with the diagonal formula: (10 × 10)/2 = 100/2 = 50 centimeters squared.
Method 2 of 4: Finding the Area of a Trapezoid
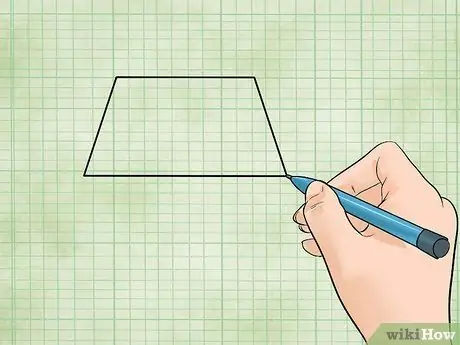
Step 1. Know how to identify a trapezoid
A trapezoid is a quadrilateral with at least 2 sides parallel to each other. The corners can have any angle. The four sides of a trapezoid may have different lengths.
There are two different ways you can find the area of a trapezoid, depending on the information you have. Below, you'll see how to use both
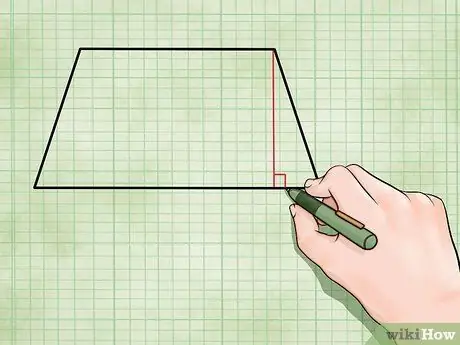
Step 2. Find the height of the trapezoid
The height of a trapezoid is a perpendicular line joining the two parallel sides. The height is usually not the same as the length of one of the sides because usually the sides are slanted. You will need the heights for both area equations. Here's how to find the height of a trapezoid:
- Find the shorter of these two base lines (parallel sides). Place your pencil at the corner point, between the base line and one of the non-parallel sides. Draw a straight line connecting the two base lines with a right angle. Measure this line to find its height.
- Sometimes you can also use trigonometry to determine the height if the height, base, and other sides form a right triangle. See our trigonometry article on right angles for more information.
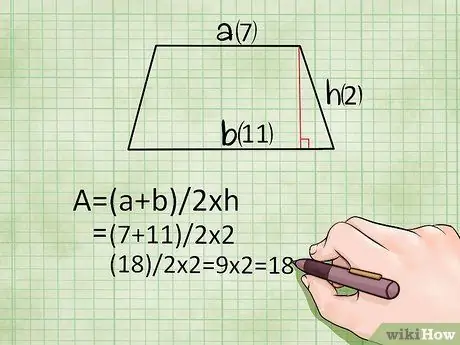
Step 3. Find the area of the trapezoid using the height and length of the base
If you know the height of the trapezoid and the lengths of its two bases, use the following equation:
- Area = (Base 1 + Base 2)/2 × height or L = (a+b)/2 × t
-
Example:
If you have a trapezoid with one base 7 meters long, the other 11 meters long, and the height line connecting the two is 2 meters long, you can find the area like this: (7 + 11)/2 × 2 = (18)/ 2 × 2 = 9 × 2 = 18 square meters.
- If the height is 10 and the base lengths are 7 and 9, you can find the area simply by doing this: (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80

Step 4. Multiply the middle segment by two to find the area of a trapezoid
The middle segment is an imaginary line parallel to the bottom and top lines of the trapezoid, and the lengths are equal to each other. Since the middle segment is always equal to (Base 1 + Base 2)/2, if you know that, you can use a quick method for the trapezoid formula:
- Area = rt × t or L = rt × t
- Basically, this is the same as using the original formula, but you use rt instead of (a + b)/2.
- ' Example:' The length of the middle segment of the trapezoid in the example above is 9 meters. This means that we can find the area of the trapezoid simply by multiplying 9 × 2 = 18 square meters, same answer as before.
Method 3 of 4: Finding the Area of a Kite

Step 1. Know how to identify a kite
A kite is a four-sided shape that has two pairs of equal sides that are adjacent to each other, not opposite each other. As the name suggests, kites resemble real kites.
There are two different ways to find the area of a kite, depending on the information you have. Below, you'll find out how to use both
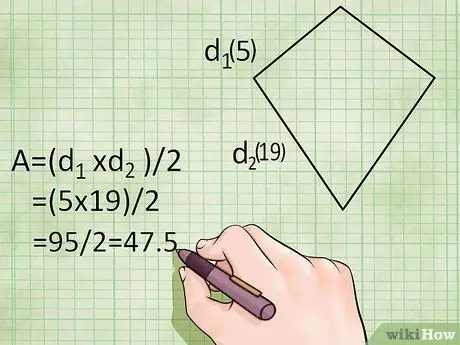
Step 2. Use the diagonal formula of a rhombus to find the area of a kite
Since a rhombus is just a special type of kite with equal sides, you can use the formula for the diagonal area of a rhombus to find the area of a kite. As a reminder, a diagonal is a straight line between two opposite corners of a kite. Just like a rhombus, the formula for the area of a kite is:
- Area = (Diag. 1 × Diag 2.)/2 or L = (d1 × d2)/2
-
Example:
If a kite has a diagonal of 19 meters and 5 meters, its area is only (19 × 5)/2 = 95/2 = 47.5 meters squared.
- If you don't know the lengths of the diagonals and can't measure them, you can use trigonometry to calculate them. Check out our kite article for more information.
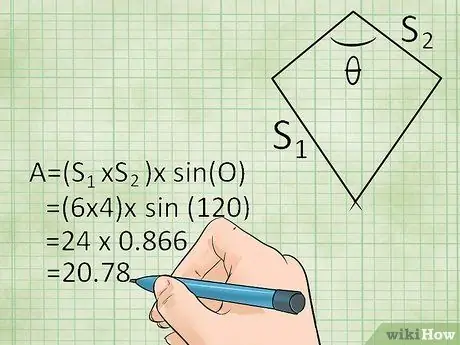
Step 3. Use the side lengths and the angle between the sides to find the area
If you know the value of the two different side lengths and the angle between the two sides, you can find the area of the kite using trigonometric principles. This method requires you to know how to do the sine function (or at least have a calculator with the sine function). Check out our trigonometry article for more information or use the formulas below:
- Area = (Side 1 × Side 2) × sin (angle) or L = (s1 × s2) × sin(θ) (where is the angle between sides 1 and 2).
-
Example:
You have a kite with two sides 6 meters long and two sides 4 meters long. The angle between the sides is 120 degrees. In this problem, you can find the area like this: (6 × 4) × sin(120) = 24 × 0.866 = 20, 78 square meters
- Note that you must use two different sides and the angle between them here - using a pair of sides of the same length will not give the correct answer.
Method 4 of 4: Solving Any Quadrant
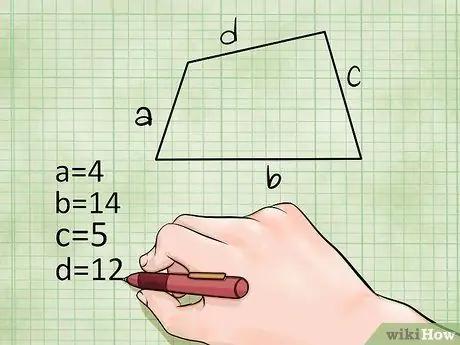
Step 1. Find the lengths of the four sides
Does your quadrilateral not fall into the categories of regular quadrilaterals above (for example, does the quadrilateral have four different lengths and have no pairs of parallel sides?) Believe it or not, there are formulas you can use to find out the area of any quadrilateral, regardless of its shape. In this section, you'll find out how to use the most common formulas. Note that this formula requires knowledge of trigonometry (again, the wikiHow article on how to use right-angled trigonometry is our guide to basic trigonometry).
- First, you have to find the lengths of the four sides of the rectangle. For the purposes of this article, we will name the sides a, b, c, and d. Sides a and c are opposite to each other and sides b and d are opposite to each other.
-
Example:
If you have a quadrilateral with odd or irregular sides that doesn't fall into any of the categories above, first, measure all four sides. Suppose the rectangle has lengths of 12, 9, 5, and 14 cm. In the steps below, you will use this information to find the area of the shape.

Step 2. Find the angles between a and d and b and c
When you're working with an irregular quadrilateral, you can't find the area just from the sides. Continue by finding the two opposite corners. For the purposes of this section, we will use angle A for the angle between sides a and d, and angle C for the angle between sides b and c. However, you can also do this with the other two opposite corners.
-
Example:
Suppose in your quadrilateral, A equals 80 degrees and C equals 110 degrees. In the next step, you will use these values to find the total area.
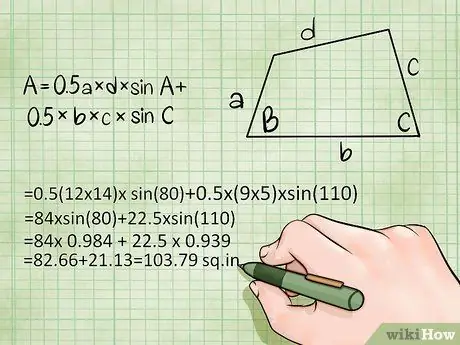
Step 3. Use the formula for the area of a triangle to find the area of a rectangle
Imagine that there is a straight line between the vertex between a and b to the vertex between c and d. This line will divide the rectangle into two triangles. Since the area of a triangle is ab sin C, where C is the angle between sides a and b, you can use this formula twice (once for each of your imaginary triangles) to get the total area of the quadrilateral. In other words, for any rectangle:
- Area = 0.5 Side 1 × Side 4 × sin(Side angle 1&4) + 0.5 × Side 2 × Side 3 × sin (Side angle 2&3) or
- Area = 0.5 a × d × sin A + 0.5 × b × c × sin C
-
Example:
You already have the sides and angles you need, so let's get this done:
-
- = 0.5 (12 × 14) × sin (80) + 0.5 × (9 × 5) × sin (110)
- = 84 × sin(80) + 22.5 × sin(110)
- = 84 × 0.984 + 22, 5 × 0, 939
- = 82, 66 + 21, 13 = 103, 79 cm squared
-
- Note that if you try to find the area of a parallelogram whose opposite angles are equal, the equation simplifies to Area = 0.5*(ad + bc) * sin A.
Tips
- This triangle calculator can easily be used to perform calculations in the "Any Quadrilateral" method above.
- For more information, check out our building-specific articles: How to Find the Area of a Square, How to Calculate the Area of a Rectangle, How to Calculate the Area of a Rhombus, How to Calculate the Area of a Trapezoid, and How to Find the Area of a Kite.






