- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
Area is a measure of an area bounded by a two-dimensional shape. Sometimes the area can be found simply by multiplying two numbers, however, it often requires more complicated calculations. Read this article for a brief explanation of the areas of quadrilaterals, triangles, circles, pyramidal and cylindrical surfaces, and the area under curved lines.
Step
Method 1 of 10: Rectangle
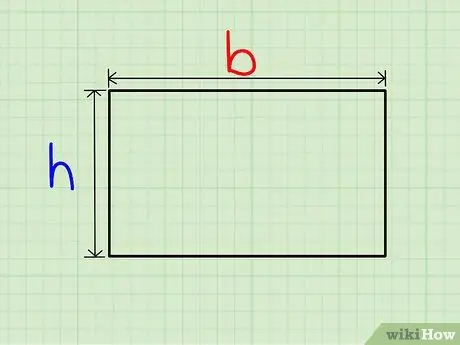
Step 1. Find the length and width of the rectangle
Since a rectangle has two pairs of equal sides, mark one as the width (l) and the other as the length (p). In general, the horizontal side is the length, and the vertical side is the width.
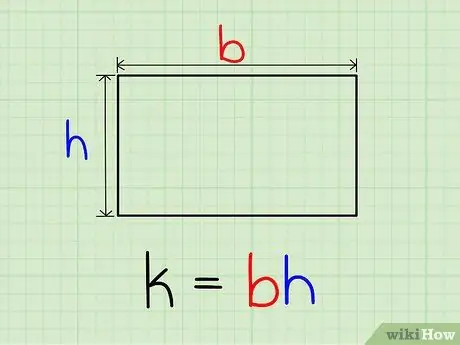
Step 2. Multiply the length and width to get the area
If the area of the rectangle is L, then L = p*l. In simple terms here, area is the product of length and width.
For a more detailed guide, read How to Find the Area of a Quadrangle
Method 2 of 10: Square

Step 1. Find the length of the side of the square
Since a square has four equal sides, all sides will be the same size.
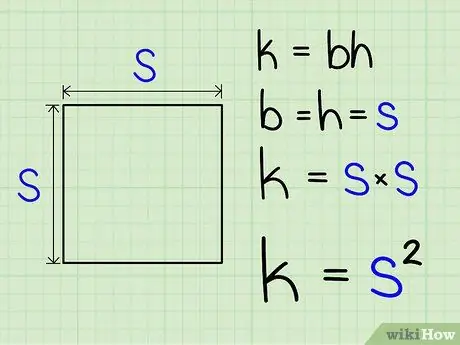
Step 2. Square the side lengths of the square
The result is breadth.
This method works because a square is basically a special quadrilateral that has the same length and width. So, in solving the formula L = p*l, p and l have the same value. So you'll end up just squaring the same number to find the area
Method 3 of 10: Parallelogram
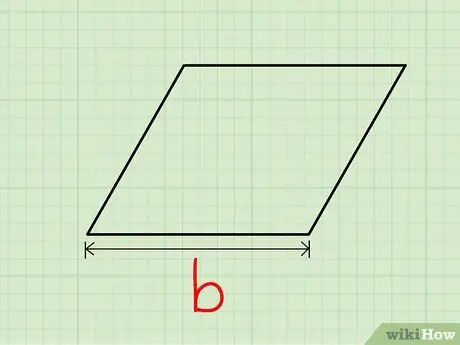
Step 1. Choose one of the sides as the base
Find the length of this base.
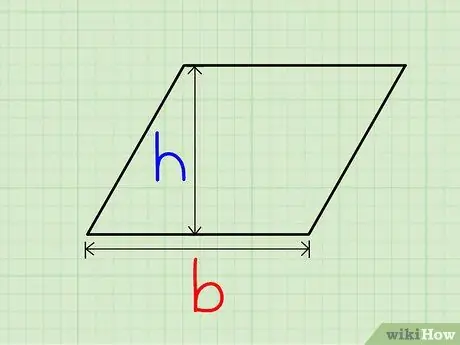
Step 2. Draw a line perpendicular to the base, and determine the length where this line meets the base and the side opposite it
This length is the height of the parallelogram.
If the side opposite the base is not long enough for the perpendiculars to not intersect, extend the side until it intersects the line
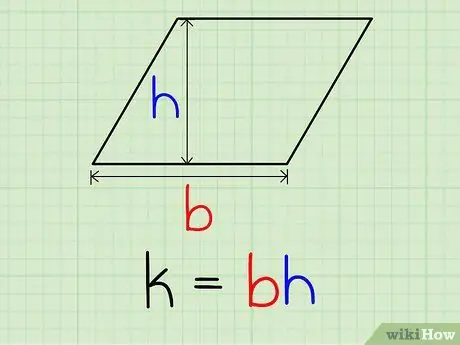
Step 3. Plug the base and height values into the equation L = a*t
For a more detailed guide, read How to Find the Area of a Parallelogram
Method 4 of 10: Trapezoid
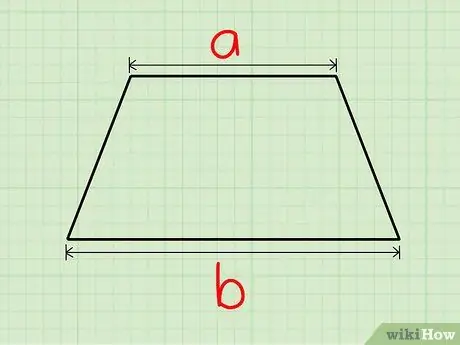
Step 1. Find the lengths of two parallel sides
Express these values as variables a and b.

Step 2. Find the height of the trapezoid
Draw a perpendicular line that intersects the two parallel sides, and the length of this line is the height of the trapezoid (t).
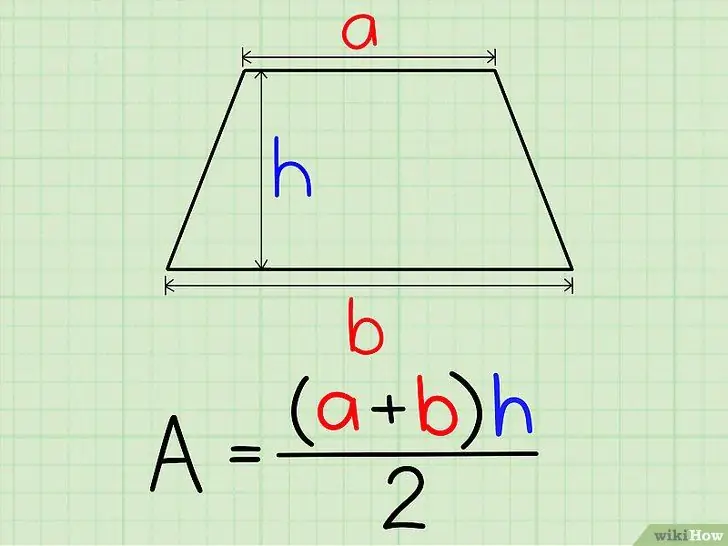
Step 3. Plug this value into the formula L = 0.5(a+b)t
For a more detailed guide, read How to Calculate the Area of a Trapezoid
Method 5 of 10: Triangle

Step 1. Find the base and height of the triangle
This value is the length of one of the sides of the triangle (the base) and the length of the perpendicular connecting the base to the hypotenuse of the triangle.
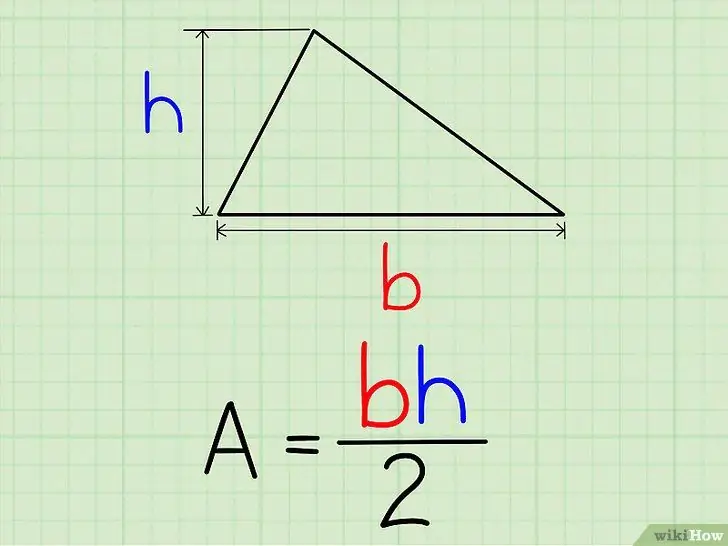
Step 2. To find the area, plug the length of the base and the height into the formula L = 0.5a*t
For more detailed information, read How to Calculate the Area of a Triangle
Method 6 of 10: Regular Polygons
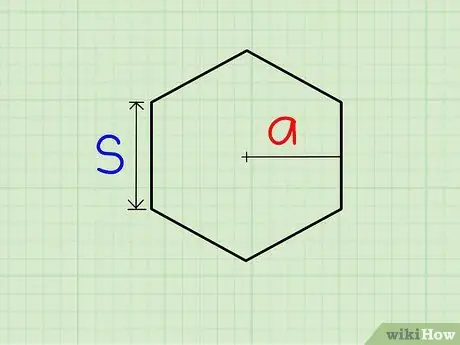
Step 1. Find the length of the side and the length of the apothem (the cut of the perpendicular line joining the midpoint of a side to the center of the polygon)
The length of the apothem will be expressed as a.
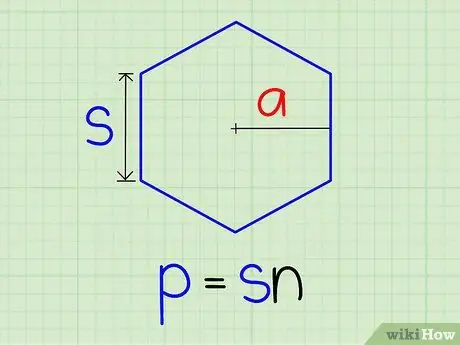
Step 2. Multiply the side length by the number of sides to get the perimeter of the polygon (K)
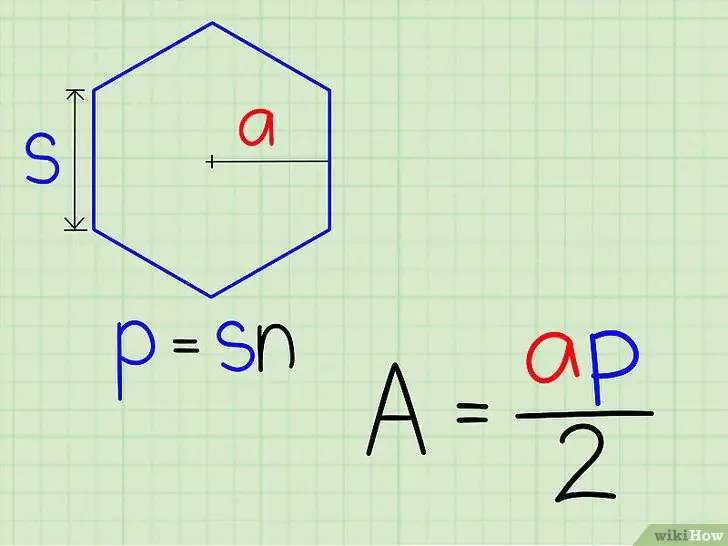
Step 3. Plug this value into the equation L = 0.5a*K
For more guidance, read How to Find the Area of a Regular Polygon
Method 7 of 10: Circle
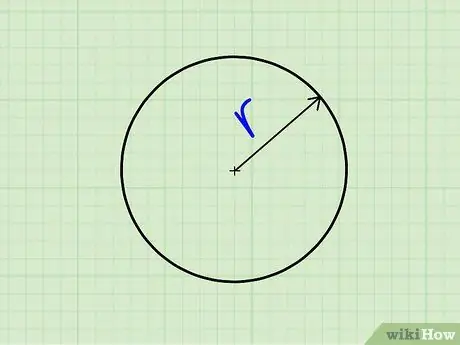
Step 1. Find the length of the radius of the circle (r)
The radius is the length that connects the center of the circle to one of the points inside the circle. Based on this explanation, the length of the radius will be the same at all points in the circle.

Step 2. Plug the radius into the equation L = r^2
For more information, read How to Calculate the Area of a Circle
Method 8 of 10: Surface Area of the Pyramid
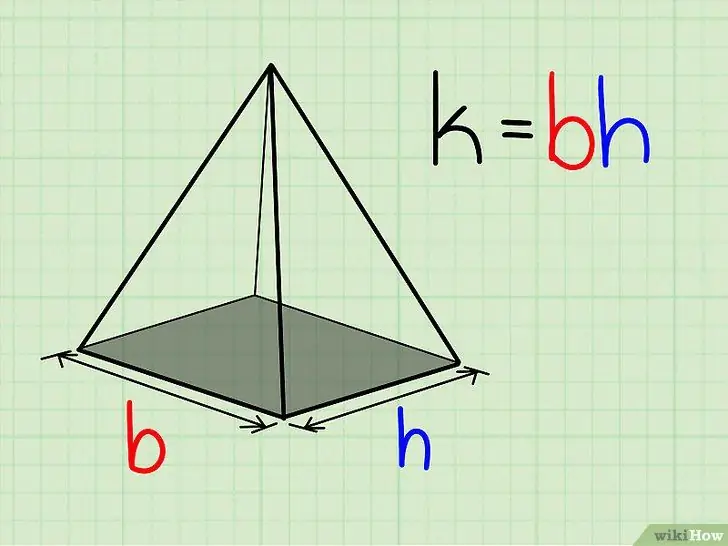
Step 1. Find the area of the base of the pyramid with the above rectangular formula L = p*l
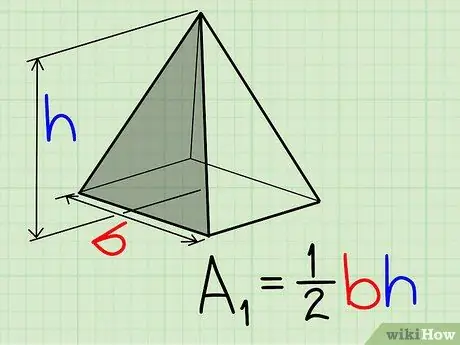
Step 2. Find the area of each triangle that makes up the pyramid with the formula for the area of the triangle above L = 0.5a*t

Step 3. Add them all together:
base and all sides.
Method 9 of 10: Cylinder Surface Area

Step 1. Find the length of the radius of the circle of the base
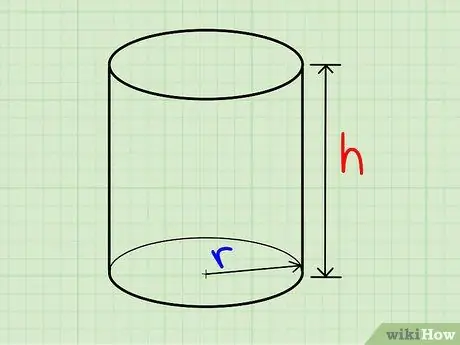
Step 2. Find the height of the cylinder

Step 3. Find the area of the base of the cylinder using the formula for the area of a circle:
L = r^2
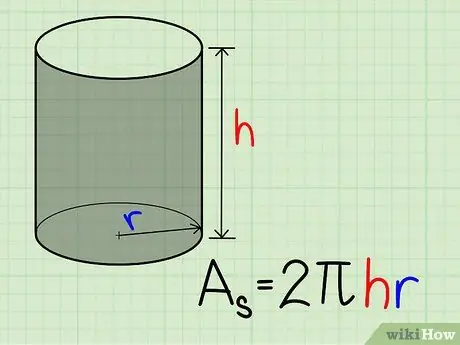
Step 4. Find the side area of the cylinder by multiplying the height of the cylinder by the circumference of the base
The circumference of a circle is K = 2πr, so the surface area of the side of the cylinder is L = 2πhr
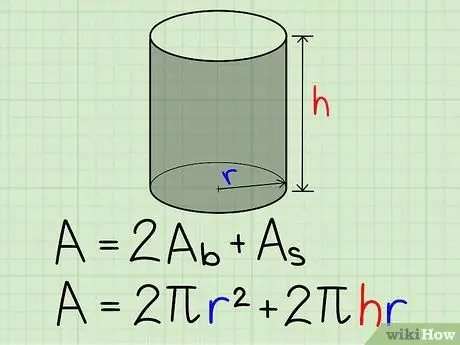
Step 5. Add up the total area:
two circles that are exactly the same, and their sides. So the surface area of the cylinder will be L = 2πr^2+2πhr.
For more detailed information, read How to Find the Surface Area of a Cylinder
Method 10 of 10: Area Under a Function
Say you need to find the area under the curve and above the x-axis expressed in the function f(x) in the range x between [a, b]. This method requires a general knowledge of calculus. If you haven't taken a calculus class before, this method may be difficult to understand.
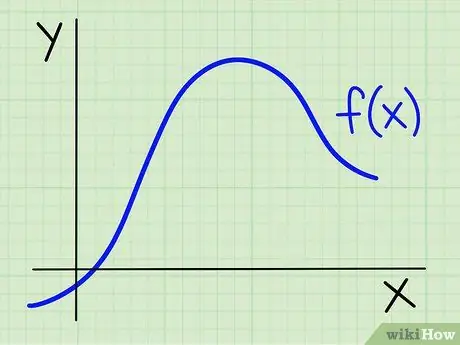
Step 1. Express f(x) by entering the value of x
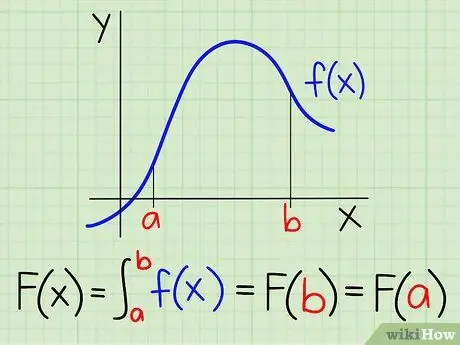
Step 2. Take the integral of f(x) between [a, b]
Using the basic theorem of calculus, F(x)=∫f(x), abf(x) = F(b)-F(a).

Step 3. Plug the values of a and b into this integral equation
The area under f(x) between x [a, b] is expressed as abf(x). So, L=F(b))-F(a).






