- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-01-23 12:04.
Surface area is the total surface area of an object, which is calculated by adding up all surfaces on the object. Finding the surface area of a 3-dimensional plane is actually quite easy as long as you know the right formula. Each field has a different formula, so first you have to determine which area to calculate the area of. Remembering the formula for the surface area of various planes will make your calculations easier in the future. The following are some of the areas that you may encounter the most in problems.
Step
Method 1 of 7: Cube

Step 1. Determine the formula for the surface area of a cube
A cube has 6 squares that are exactly the same. The length and width of the square are the same, so the surface area is a2, where a is the side length of the square. The formula for the surface area (L) of a cube is L = 6a2, where a is the length of one of the sides.
The unit of surface area is the unit of square length, namely: in2, cm2, m2, etc.

Step 2. Measure the length of one side of the cube
Each side or edge of the cube is the same length as the other, so you only need to measure one side. Use a ruler to measure the side lengths of the cube. Pay attention to the unit of length you use.
- Express this measure as the value of a.
- Example: a = 2 cm

Step 3. Square the result of measure a
Square the length of the edge of the cube. Squaring means multiplying by the number itself. When you're first learning this formula, writing the area formula as L= 6*a*a might help.
- Note: this step only calculates one side of the cube.
- Example: a = 2 cm
- a2 = 2 x 2 = 4 cm2

Step 4. Multiply the result of the above calculation by 6
Remember that a cube has 6 identical sides. Once you know one side of the cube, you have to multiply it by 6 to calculate all six sides.
- This step completes the calculation of the surface area of the cube.
- Example: a2 = 4 cm2
- Surface area = 6 x a2 = 6 x 4 = 24 cm2
Method 2 of 7: Block

Step 1. Determine the formula for the surface area of a cuboid
Just like cubes, cubes also have 6 sides. However, unlike a cube, the sides on a cuboid are not identical. In blocks, only opposite sides are equal. As a result, the surface area of the cuboid must be calculated according to the lengths of the different sides, and the formula is L = 2ab + 2bc + 2ac.
- In this formula, a is the width of the block, b is the height, and c is the length.
- Pay attention to the formula above and you will understand that to calculate the surface area of a cuboid, you just need to add up all the sides.
- The unit of surface area is the unit of square length: in2, cm2, m2, etc.

Step 2. Measure the length, height, and width of each side of the block
These three measurements may differ, so measurements of all three must be taken separately. Use a ruler to measure each side and record the results. Use the same units in all measurements.
- Measure the length of the base of the block to determine its length, and express it as c.
- Example: c = 5 cm
- Measure the width of the base of the block to determine its width, and express it as a.
- Example: a = 2 cm
- Measure the side height of the block to determine its height, and express it as b.
- Example: b = 3 cm
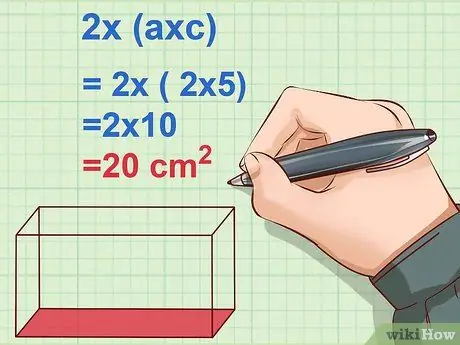
Step 3. Calculate the area of one side of the block then multiply by 2
Remember that there are 6 sides of the block, but only the opposite sides are identical. Multiply length and height or c and a to find the surface area of one side of the block. Multiply the result by 2 to calculate the two identical sides.
Example: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 cm2
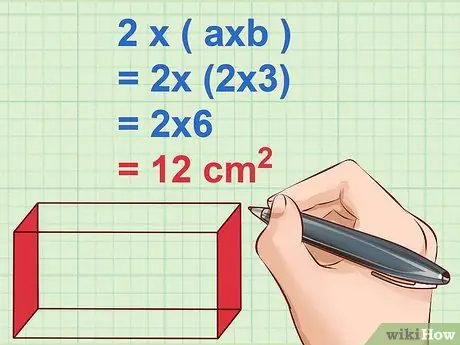
Step 4. Find the surface area of the other side of the block and multiply it by 2
Just like the previous pair of sides, multiply the width and height, or a and b to find the surface area of the other block. Multiply the result by 2 to calculate the two identical opposite sides.
Example: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 cm2
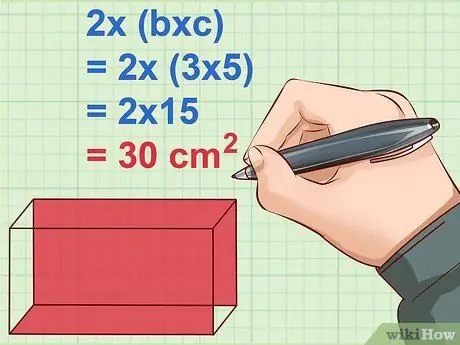
Step 5. Calculate the surface area of the last side of the block and multiply by 2
The last two sides of the block are the sides. Multiply length and width or c and b to find it. Multiply the result by 2 to calculate both sides.
Example: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 cm2

Step 6. Add up the results of the three calculations
The surface area is the total area of all the sides of the object, so the last step in the calculation is to add up all the results of the previous calculations. Add up the area of all the sides of the cuboid to find the surface area.
Example: Surface area = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 cm2.
Method 3 of 7: Triangular Prism
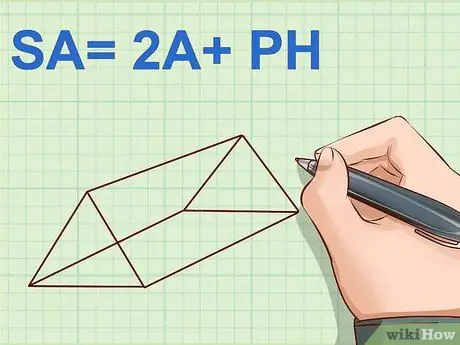
Step 1. Determine the formula for the surface area of a triangular prism
A triangular prism has 2 identical triangular sides and 3 rectangular sides. To find the surface area, you have to calculate the area of all these sides and then add them up. The surface area of a triangular prism is L = 2A + PH, where A is the area of the triangular base, P is the perimeter of the triangular base, and H is the height of the prism.
- In this formula, A is the area of the triangle calculated according to the formula A = 1/2bh where b is the base of the triangle and h is the height.
- P is the perimeter of the triangle which is calculated by adding up the three sides of the triangle.
- The unit of surface area is one unit of square length: in2, cm2, m2, etc.
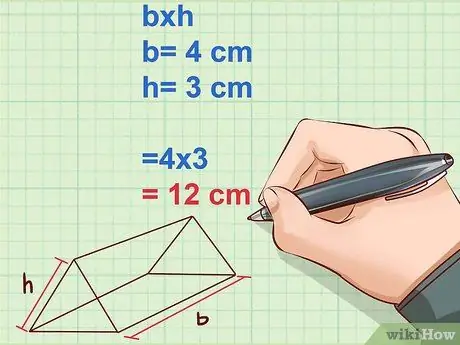
Step 2. Calculate the area of the side of the triangle and multiply by 2
The area of a triangle can be calculated by the formula 1/2b*h where b is the base of the triangle and h is the height. The two sides of the triangle in a prism are identical so we can multiply them by 2. This will make the area calculation simpler, i.e. b*h.
- The base of the triangle or b is equal to the length of the base of the triangle.
- Example: b = 4 cm
- The height or h of the base of the triangle is equal to the distance between the base and the vertex of the triangle.
- Example: h = 3 cm
- Multiply the area of one of the triangles by 2 to get 2(1/2)b*h = b*h = 4*3 =12 cm

Step 3. Measure each side of the triangle and the height of the prism
To complete the surface area calculation, you need to know the length of each side of the triangle and the height of the prism. The height of the prism is the distance between the two sides of the triangle.
- Example: H = 5 cm
- The three sides in this calculation are the three sides of the triangle's base.
- Example: S1 = 2 cm, S2 = 4 cm, S3 = 6 cm

Step 4. Determine the perimeter of the triangle
The perimeter of a triangle can be calculated easily by adding up all the sides that have been measured in length, namely: S1 + S2 + S3.
Example: P = S1 + S2 + S3 = 2 + 4 + 6 = 12 cm

Step 5. Multiply the perimeter of the base by the height of the prism
Remember the height of the prism is the distance between the two sides of the triangle. Or in other words, multiply P by H.
Example: W x H = 12 x 5 = 60 cm2

Step 6. Add up the two previous measurement results
You must add the two calculations in the previous step to calculate the surface area of a triangular prism.
Example: 2A + PH = 12 + 60 = 72 cm2.
Method 4 of 7: Ball

Step 1. Determine the formula for the surface area of a sphere
A sphere is made up of curved circles, so calculating its area must use the mathematical constant pi. The surface area of the sphere is calculated by the formula L = 4π*r2.
- In this formula, r is equal to the radius of the sphere. Pi or, can be rounded to 3, 14.
- The unit of surface area is the unit of square length: in2, cm2, m2, etc.

Step 2. Measure the length of the radius of the ball
The radius of the sphere is half its diameter, or half the distance between the two sides of the sphere through its center.
Example: r = 3 cm
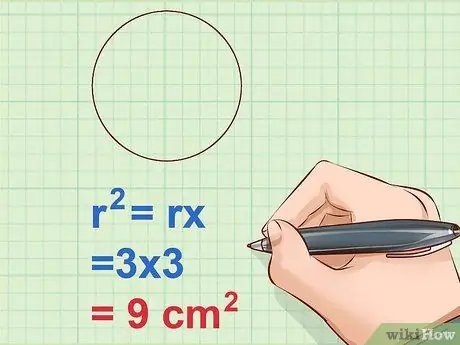
Step 3. Square the radius of the ball
To square a number, you just need to multiply it by the number itself. So multiply the length of r by the same value. Remember that this formula can be written as L = 4π*r*r.
Example: r2 = r x r = 3 x 3 = 9 cm2

Step 4. Multiply the square of the radius by rounding the value of pi
Pi is a constant that represents the ratio of the circumference of a circle to its diameter. Pi is an irrational number that has many decimal places so it is often rounded up to 3.14. Multiply the square of the radius by pi or 3.14 to find the surface area of one of the circles on the sphere.
Example: *r2 = 3, 14 x 9 = 28, 26 cm2

Step 5. Multiply the result of the above calculation by 4
To complete the calculation, multiply the value in the previous step by 4. Find the surface area of the sphere by multiplying the side of the flat circle by 4.
Example: 4π*r2 = 4 x 28, 26 = 113, 04 cm2
Method 5 of 7: Cylinder

Step 1. Determine the formula for the surface area of a cylinder
Cylinders have 2 circular sides and 1 curved side. The formula for the surface area of a cylinder is L = 2π*r2 + 2π*rh, where r is the radius of the circle and h is the height of the cylinder. Round pi or to 3, 14.
- 2π*r2 is the area of the two sides of the circle, while 2πrh is the area of the curved side that connects the two circles on the cylinder.
- The unit of area is the unit of square length: in2, cm2, m2, etc.
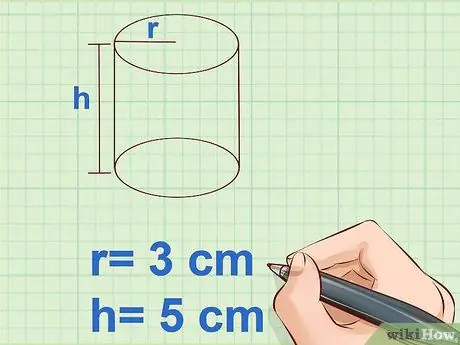
Step 2. Measure the radius and height of the cylinder
The radius of a circle is equal to half the length of the diameter, or half the distance from one side to the other through the center of the circle. Height is the distance between the base and the top of the cylinder. Use a ruler to measure and record the results.
- Example: r = 3 cm
- Example: h = 5 cm

Step 3. Find the area of the base of the cylinder and multiply by 2
To find the area of the base of a cylinder you only need to use the formula for the area of a circle or *r2. To complete the calculation, square the radius of the circle and multiply by pi. Then multiply by 2 to calculate the two sides of the circle that are identical at both ends of the cylinder.
- Example: area of base of cylinder = *r2 = 3, 14 x 3 x 3 = 28, 26 cm2
- Example: 2π*r2 = 2 x 28, 26 = 56, 52 cm2

Step 4. Calculate the curved side area of the cylinder using the formula 2π*rh
This formula is used to calculate the surface area of a cylinder. The tube is the space between the two sides of the circle on the cylinder. Multiply the radius by 2, pi, and the height of the cylinder.
Example: 2π*rh = 2 x 3, 14 x 3 x 5 = 94, 2 cm2

Step 5. Add up the two previous measurements
Add the surface area of the two circles to the area of the curved area between the two circles to find the surface area of the cylinder. Note, adding up the two results of this calculation will satisfy the original formula: L =2π*r2 + 2π*rh.
Example: 2π*r2 + 2π*rh = 56, 52 + 94, 2 = 150, 72 cm2
Method 6 of 7: Square Pyramid

Step 1. Determine the surface area of the square pyramid
A square pyramid has a square base and 4 triangular sides. Remember, the area of a square can be calculated by squaring one of its sides. The area of a triangle is 1/2sl (base times the height of the triangle divided by 2). There are 4 triangular areas in the pyramid, so to find the total surface area, you must multiply the area of the triangle by 4. Adding all the sides of this square pyramid gives the formula for the surface area: L = s2 + 2sl.
- In this formula, s represents the length of each side of the square on the base of the pyramid, and l represents the height of the hypotenuse of the triangle.
- The unit of surface area is the unit of square length: in2, cm2, m2, etc.

Step 2. Measure the height and base of the hypotenuse of the pyramid
The height of the hypotenuse of the pyramid, or l, is the height of one of the sides of the triangle. This value is the distance between the base and the top of the pyramid from one of the horizontal sides. The side of the base of the pyramid or s, is the length of one of the sides of the square on the base. Use a ruler to measure the required length of each side.
- Example: l = 3 cm
- Example: s = 1 cm
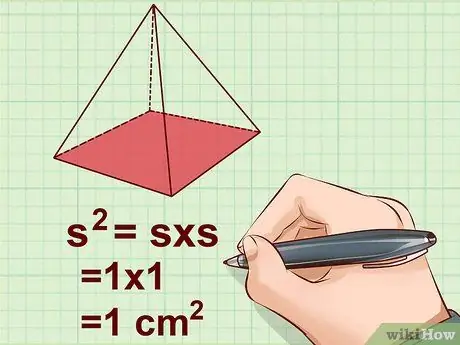
Step 3. Find the area of the base of the pyramid
The area of the base of the pyramid can be calculated by squaring the length of one of its sides, or multiplying the value of s by the same value.
Example: s2 = s x s = 1 x 1 = 1 cm2
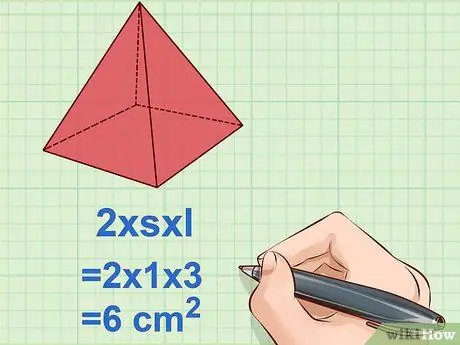
Step 4. Calculate the surface area of the four sides of the triangle
The second part of the formula is calculating the area of the four sides of the triangle. According to the 2ls formula, multiply s by l and 2. This will give you the area of each side of the pyramid.
Example: 2 x s x l = 2 x 1 x 3 = 6 cm2
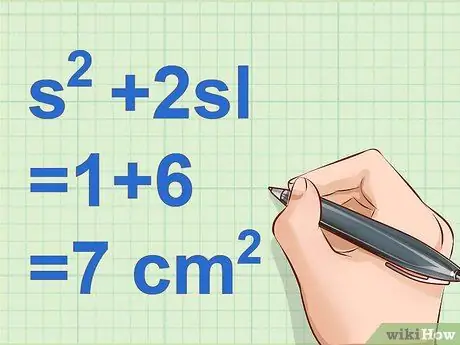
Step 5. Add up the two previous calculations
Add up the total area of the hypotenuse with the base to find the surface area of the pyramid.
Example: s2 + 2sl = 1 + 6 = 7 cm2
Method 7 of 7: Cones

Step 1. Determine the formula for the area of a cone
A cone has a circular base and a curved plane that tapers off at one point. To find the surface area, you have to calculate the area of the circular base and the conical curved area, then add them together. The formula for the surface area of a cone is: L = *r2 + *rl, where r is the radius of the circle's base, l is the height of the hypotenuse of the cone, and is the mathematical constant pi (3, 14).
The unit of area is the unit of square length: in2, cm2, m2, etc.
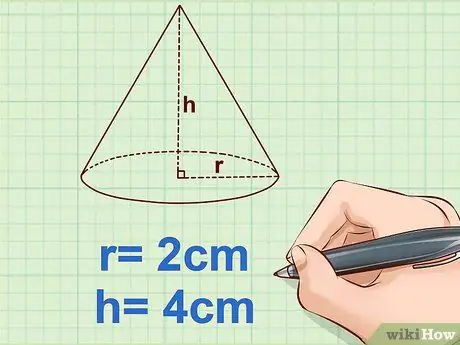
Step 2. Measure the radius and height of the cone
The radius is the distance between the center of the circle and its edges. Height is the distance from the center of the base to the top of the cone.
- Example: r = 2 cm
- Example: h = 4 cm

Step 3. Calculate the height of the hypotenuse of the cone (l)
The height of the hypotenuse is basically the hypotenuse of the triangle, so you have to use the Pythagorean Theorem to calculate it. Use the adjusted formula that is l = (r2 + h2), where r is the radius and h is the height of the cone.
Example: l = (r2 + h2) = (2 x 2 + 4 x 4) = (4 + 16) = (20) = 4.47 cm

Step 4. Determine the area of the base of the cone
The area of the base of the cone can be calculated by the formula *r2. After measuring the radius, square it (multiply by the value itself), then multiply the result by pi.
Example: *r2 = 3, 14 x 2 x 2 = 12, 56 cm2

Step 5. Calculate the curved area of the cone
Using the formula *rl, where r is the radius of the circle, and l the height of the hypotenuse calculated in the previous step, you can calculate the area of the curved side of the cone.
Example: *rl = 3, 14 x 2 x 4, 47 = 28, 07 cm

Step 6. Add up the two previous calculations to find the surface area of the cone
Calculate the surface area of a cone by adding up the area of the base and the area of the curved side.
Example: *r2 + *rl = 12, 56 + 28, 07 = 40, 63 cm2
What You Need
- Ruler
- Pen or pencil
- Paper
Related wikiHow Articles
- Calculating the Entire Surface Area of the Tube
- Finding the Surface Area of a Cube






