- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
Grouping is a special technique used to factor polynomial equations. You can use it with quadratic equations and polynomials that have four terms. The two methods are almost the same, but slightly different.
Step
Method 1 of 2: Quadratic Equation

Step 1. Look at the equation
If you plan to use this method, the equation must follow the basic form: ax2 + bx + c
- This process is usually used when the leading coefficient (a term) is a number other than "1", but it can also be used for quadratic equations where a = 1.
- Example: 2x2 + 9x + 10
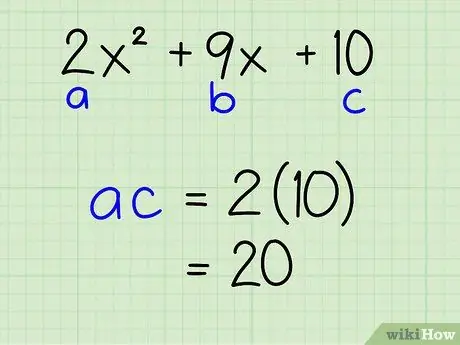
Step 2. Find the main product of
Multiply the terms a and c. The product of these two terms is called the principal product.
-
Example: 2x2 + 9x + 10
- a = 2; c = 10
- a * c = 2 * 10 = 20
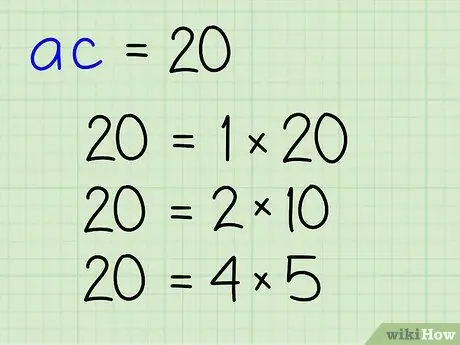
Step 3. Separate the product into its factor pairs
Write down the factors of your main product by separating them into pairs of integers (the pairs needed to get the main product).
-
Example: The factors of 20 are: 1, 2, 4, 5, 10, 20
Written in pairs of factors: (1, 20), (2, 10), (4, 5)

Step 4. Find a pair of factors with a sum equal to b
Look in the factor pairs and determine the pair that will give the b term - the median term and the x coefficient - when added together.
- If your main product is negative, you'll need to find a pair of factors that equal the term b when subtracted from each other.
-
Example: 2x2 + 9x + 10
- b = 9
- 1 + 20 = 21; this is not the right couple
- 2 + 10 = 12; this is not the right couple
- 4 + 5 = 9; this is true partner
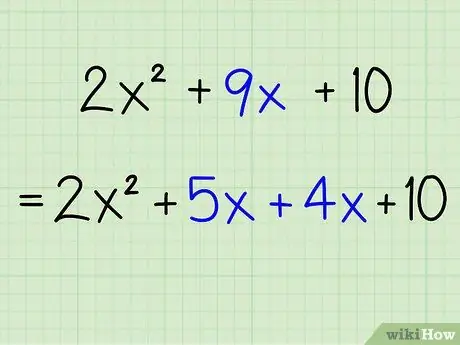
Step 5. Split the middle term into two factors
Rewrite the middle term by separating it into the factor pairs that were previously searched for. Make sure you enter the correct sign (plus or minus).
- Note that the order of the middle terms is not important for this problem. No matter the order of the terms you write, the result will be the same.
- Example: 2x2 + 9x + 10 = 2x2 + 5x + 4x + 10
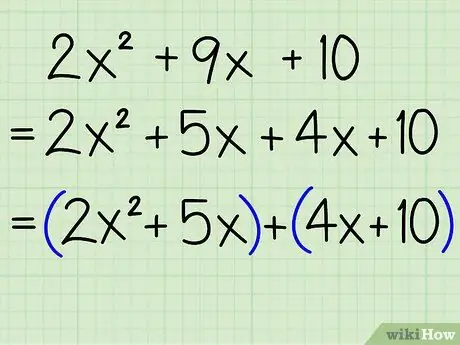
Step 6. Group the tribes to form pairs
Group the first two terms into one pair and the second two terms into one pair.
Example: 2x2 + 5x + 4x + 10 = (2x2 + 5x) + (4x + 10)

Step 7. Factor each pair
Find the common factors of the pair and factor them out. Rewrite the equation correctly.
Example: x(2x + 5) + 2(2x + 5)
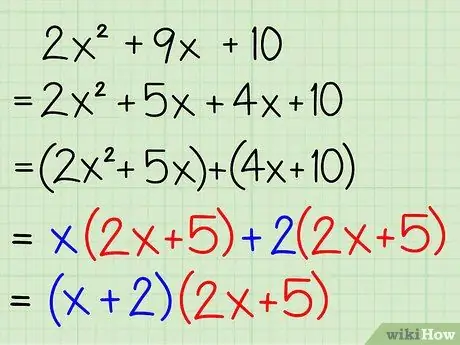
Step 8. Factor out the equal brackets
There should be the same binomial brackets between the two halves. Factor these brackets out and put the other terms inside the other brackets.
Example: (2x + 5)(x + 2)
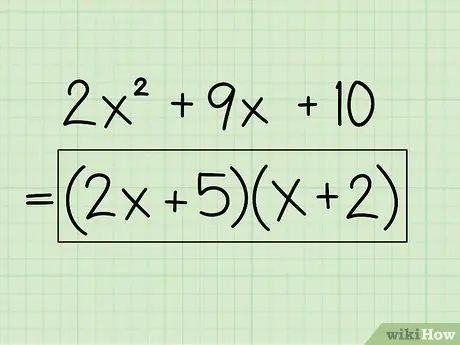
Step 9. Write down your answers
Now you have your answer.
-
Example: 2x2 + 9x + 10 = (2x + 5)(x + 2)
The final answer is: (2x + 5)(x + 2)
Additional Examples

Step 1. Factor:
4x2 - 3x - 10
- a * c = 4 * -10 = -40
- Factors of 40: (1, 40), (2, 20), (4, 10), (5, 8)
- The correct pair of factors: (5, 8); 5 - 8 = -3
- 4x2 - 8x + 5x - 10
- (4x2 - 8x) + (5x - 10)
- 4x(x - 2) + 5(x - 2)
- (x - 2)(4x + 5)

Step 2. Factor:
8x2 + 2x - 3
- a * c = 8 * -3 = -24
- Factor of 24: (1, 24), (2, 12), (4, 6)
- The correct pair of factors: (4, 6); 6 - 4 = 2
- 8x2 + 6x - 4x - 3
- (8x2 + 6x) - (4x + 3)
- 2x(4x + 3) - 1(4x + 3)
- (4x + 3)(2x - 1)
Method 2 of 2: Polynomials with Four Terms
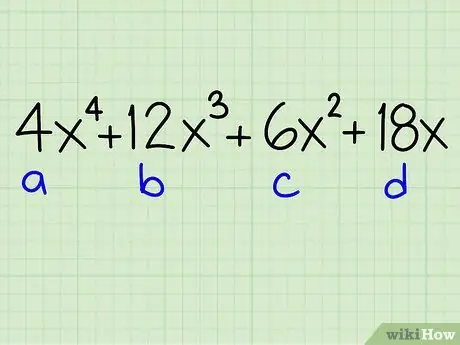
Step 1. Look at the equation
The equation should have four separate terms. However, the form of the four tribes can vary.
- Usually, you'll use this method if you see a polynomial equation that looks like: ax3 + bx2 + cx + d
-
The equation can also look like:
- axy + by + cx + d
- ax2 + bx + cxy + dy
- ax4 + bx3 + cx2 + dx
- Or almost the same variation.
- Example: 4x4 + 12x3 + 6x2 + 18x
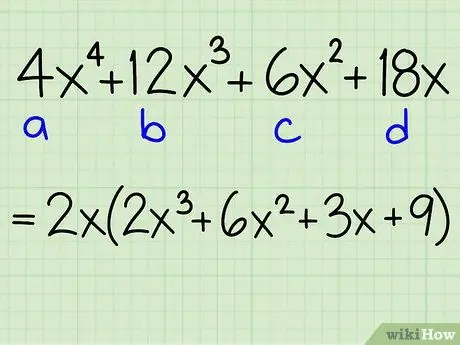
Step 2. Factor out the greatest common factor (GCF)
Determine if the four terms have anything in common. The greatest common factor of the four terms, if any are common, must be factored out of the equation.
- If the only thing the four terms have in common is the number "1", then that term has no GCF and nothing can be factored out at this step.
- When you factor out the GCF, make sure that you continue to write that GCF at the front of your equation as you work. This out-factored GCF must be included as part of your final answer for your answer to be accurate.
-
Example: 4x4 + 12x3 + 6x2 + 18x
- Each term is equal to 2x, so this problem can be rewritten as:
- 2x(2x3 + 6x2 +3x+9)
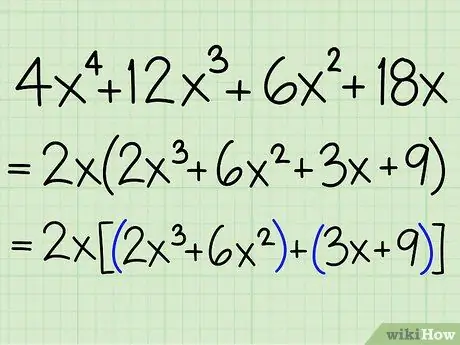
Step 3. Make smaller groups in the problem
Group the first two terms and the second two terms.
- If the first term of the second group has a minus sign in front of it, you must place the minus sign in front of the second parenthesis. You have to change the sign of the second term in the second group to match it.
- Example: 2x(2x3 + 6x2 + 3x + 9) = 2x[(2x3 + 6x2) + (3x + 9)]
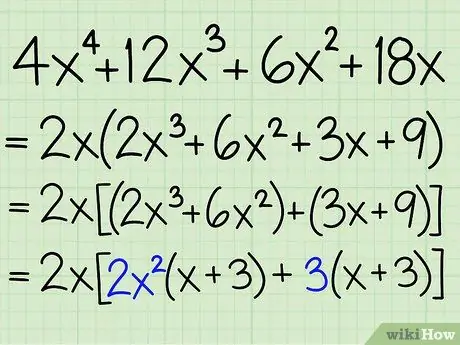
Step 4. Factor out the GCF from each binomial
Identify the GCF in each binomial pair and factor the GCF to be outside the pair. Rewrite this equation correctly.
-
At this step, you may be faced with the choice between factoring out positive or negative numbers for the second group. Look at the signs before the second and fourth terms.
- When both signs are the same (both positive or both negative), factor out a positive number.
- When the two signs are different (one negative and one positive), factor out a negative number.
- Example: 2x[(2x3 + 6x2) + (3x + 9)] = 2x2[2x2(x + 3) + 3(x + 3)]
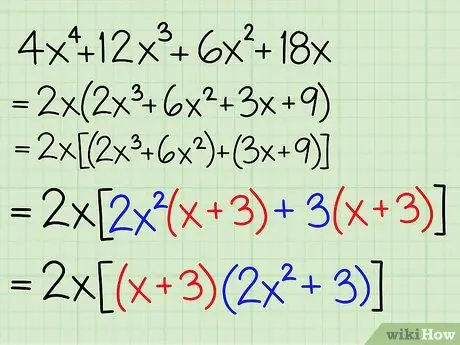
Step 5. Factor out the same binomial
The binomial pairs in both brackets must be the same. Factor this pair out of the equation, then group the remaining terms into other parentheses.
- If the binomials in parentheses don't match, double-check your work or try rearranging your terms and regrouping the equation.
- All brackets must be the same. If they are not the same, then the problem will not be factored by grouping or other methods even if you try any method.
- Example: 2x2[2x2(x + 3) + 3(x + 3)] = 2x2[(x + 3)(2x2 + 3)]
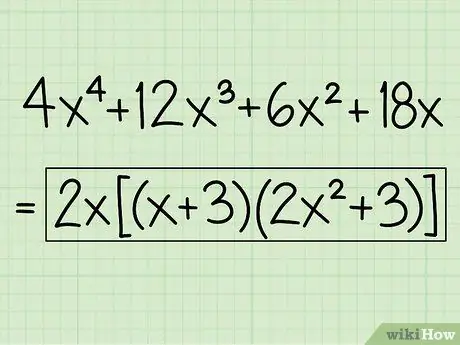
Step 6. Write down your answers
You will have your answer at this step.
-
Example: 4x4 + 12x3 + 6x2 + 18x = 2x2(x + 3)(2x2 + 3)
The final answer is: 2x2(x + 3)(2x2 + 3)
Additional Examples

Step 1. Factor:
6x2 + 2xy - 24x - 8y
- 2[3x2 +xy - 12x - 4y]
- 2[(3x2 +xy) - (12x + 4y)]
- 2[x(3x + y) - 4(3x + y)]
- 2[(3x + y)(x - 4)]
- 2(3x + y)(x - 4)

Step 2. Factor:
x3 - 2x2 + 5x - 10
- (x3 - 2x2) + (5x - 10)
- x2(x - 2) + 5(x - 2)
- (x - 2)(x2 + 5)






