3 Ways to Parse Numbers

2024 Author: Jason Gerald | [email protected]. Last modified: 2023-12-16 10:50

Numerical dissection exercises allow young students to understand patterns and relationships between digits in larger numbers and between numbers in an equation. You can break numbers down into their hundreds, tens, and ones places, or you can break them down by breaking them down into various numbers in addition.

Step

Method 1 of 3: Breaking down into Places of Hundreds, Tens, and Units

Step 1. Understand the difference between "tens" and "ones"

When you see a number with two digits without a decimal point, the two digits represent the “tens” place and the “ones” place. The “tens” place is on the left and the “ones” place is on the right.

Numbers in the “units” place can be read as they appear. The numbers included in the “ones” place are all the numbers from 0 to 9 (zero, one, two, three, four, five, six, seven, eight, and nine).
Numbers in the “tens” place only look like numbers in the “ones” place. However, when viewed separately, this number actually has a 0 behind it, making it larger than the number in the "ones" place. Numbers included in the “tens” place include: 10, 20, 30, 40, 50, 60, 70, 80, and 90 (ten, twenty, thirty, forty, fifty, sixty, seventy)., eighty, and ninety).

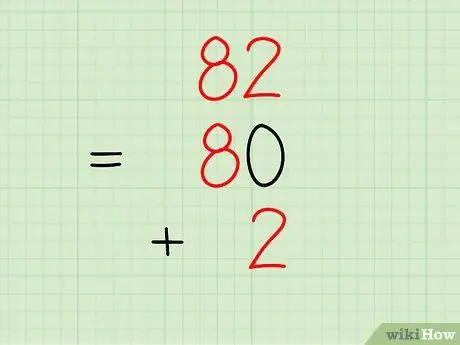
Step 2. Spread the two-digit number

When you are given a number with two digits, it has a “ones” place part and a “tens” place part. To decipher this number, you must break it down into its separate parts.

Example: Describe the number 82.
- 8 is in the “tens” place so this part of the number can be separated and written as 80.
- 2 is in the “units” place, so this part of the number can be separated and written as 2.
- When writing down your answer, you would write: 82 = 80 + 2
Also note that numbers written in the normal way are numbers written in their "standard form," but numbers spelled out are written in their "translated form."

Based on the previous example, "82" is the standard form and "80 + 2" is the translated form

Step 3. Understand about "hundreds" places

When a number has three digits without a decimal point, it has a “ones” place, a “tens” place, and a “hundreds” place. The “hundreds” place is to the left of the number. The “tens” place is in the middle, and the “ones” place remains to the right.

Numbers where “ones” and “tens” work exactly the same as when you have a two-digit number.
A number in the “hundreds” place will look like a number in the “ones” place, but when viewed separately, the number in the “hundreds” place actually has two trailing zeros. The numbers included in the "hundreds" place position are: 100, 200, 300, 400, 500, 600, 700, 800, and 900 (one hundred, two hundred, three hundred, four hundred, five hundred, six hundred, seven hundred, eight hundred and nine hundred).

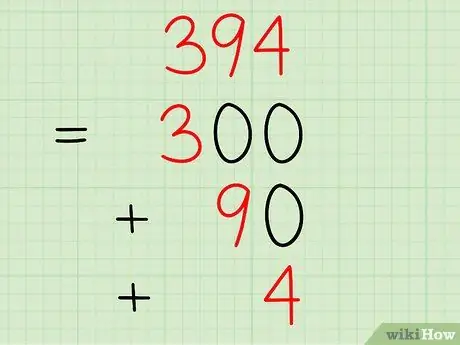
Step 4. Spread the three-digit number

When you are given a three-digit number, it has a “ones” place part, a “tens” place part, and a “hundreds” place part. To decipher a number this large, you must break it down into its three parts.

Example: Parse the number 394.
- 3 is in the “hundreds” place, so this part of the number can be separated and written as 300.
- 9 is in the “tens” place, so this part of the number can be separated and written as 90.
- 4 is in the “units” place, so this part of the number can be separated and written as 4.
- Your final written answer will look like: 394 = 300 + 90 + 4
- When written as 394, the number is written in its standard form. When written as 300 + 90 + 4, the number is written in its translation form.

Step 5. Apply this pattern to the larger numbers, which are infinity

You can decompose larger numbers using the same principle.

Digits in any position can be broken down into their separate parts by substituting the numbers to the right of the digits containing zeros. This applies to all numbers, no matter how large they are.
Example: 5,394,128 = 5,000,000 + 300,000 + 90,000 + 4,000 + 100 + 20 + 8

Step 6. Understand how decimals work

You can parse decimal numbers, but any number after the decimal point must be parsed into its position part, which is also represented by a decimal point.

The “tenths” position is used for single digits immediately after (to the right of) the decimal point.
The “hundredths” position is used when there are two digits to the right of the decimal point.
The “thousands” position is used when there are three digits to the right of the decimal point.

Step 7. Spread the decimal numbers

When you have a number that has digits to the left and right of the decimal point, you must parse it by spreading out both sides.

Note that all numbers that appear to the left of the decimal point can still be parsed in the same way as parsing when the number does not have a decimal point.
Example: Parse the numbers 431, 58
- 4 is in the “hundreds” place, so 4 should be separated and written as: 400
- 3 is in the “tens” place, so 3 should be separated and written as: 30
- 1 is in the “units” place, so 1 should be separated and written as: 1
- 5 is in the “tithes” place, so 5 should be separated and written as: 0.5
- 8 is in the “hundreds” place, so 8 should be separated and written as: 0.08
- The final answer can be written as: 431.58 = 400 + 30 + 1 + 0.5 + 0.08

Method 2 of 3: Breaking into Multiple Numbers in Addition

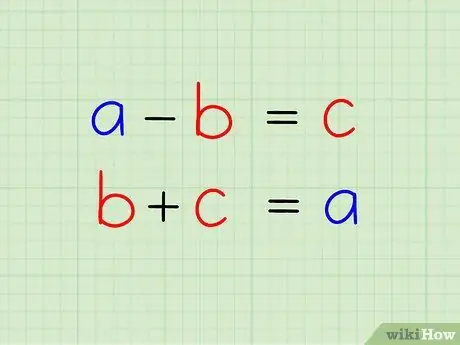
Step 1. Understand the concept

When you break a number into various numbers in the addition, you break the number into different sets of other numbers (the numbers in the addition), which can be added together to get the initial value.

When one of the numbers in the addition is subtracted from the initial number, the second number must be the answer you get.
When the two numbers in the addition are added together, the initial number must be the result of the sum you calculated.

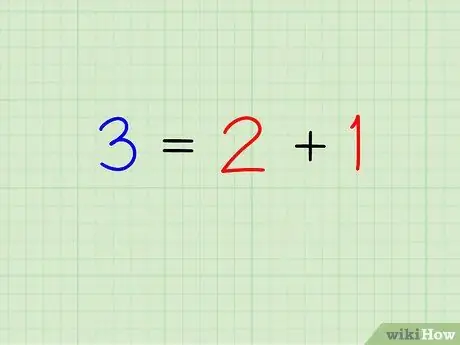
Step 2. Practice with small numbers

This exercise is easiest to do if you have a single-digit number (a number that only has a “ones” place).

You can combine the principles learned here with the principles learned in the section “Decomposing into Places of Hundreds, Tens, and Units” when you need to decompose larger numbers. However, because there are so many possible combinations of numbers in the sum, this method becomes less practical to use when working with large numbers

Step 3. Work all the combinations of numbers in different additions

To decompose a number into the numbers in its addition, all you have to do is write down all the different possible ways to generate the original number using smaller numbers and addition.

Example: Break the number 7 into numbers in different additions.
- 7 = 0 + 7
- 7 = 1 + 6
- 7 = 2 + 5
- 7 = 3 + 4
- 7 = 4 + 3
- 7 = 5 + 2
- 7 = 6 + 1
- 7 = 7 + 0

Step 4. Use visuals, if needed

For someone trying to learn this concept for the first time, it might help to use visuals that demonstrate the process in a practical and active way.

Start with the initial amount of an item. For example, if the number is seven, you can start with seven candies.
- Separate the candy pile into two different piles by moving one candy pile to the other. Count the remaining candies in the second pile and explain that the initial seven candies have been broken down into “one” and “six”.
- Continue separating the candies into two separate piles by gradually picking up the candies from the initial pile and adding them to the second pile. Count the number of candies in both piles in each move.
This can be done with several different materials, including small candies, square paper, colored clothes pins, blocks, or buttons.

Method 3 of 3: Deciphering the Equation

Step 1. Look at a simple addition equation

You can combine decomposition methods to break these types of equations into different forms.

This method is easiest to use for simple addition equations, but it becomes less practical when used for long equations

Step 2. Break down the numbers in the equation

Look at the equation and break down the numbers into separate "tens" and "ones" places. If needed, you can define "units" further by breaking them down into smaller parts.

Example: Solve and solve the equation: 31 + 84
- You can decompose 31 to: 30 + 1
- You can decompose 84 to: 80 + 4

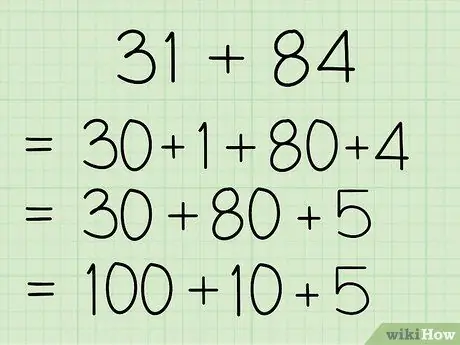
Step 3. Convert and rewrite the equation into an easier form

The equation can be rewritten so that each of the elements described stands alone, or you can combine certain elements described to help you understand the equation as a whole better.