- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-01-23 12:04.
In a chemical reaction, matter can neither be created nor destroyed, so the products of a reaction must be equal to the number of reactants in the reaction. Stoichiometry is the study of the quantitative relationship of the elements in a reaction, which involves calculating the mass of the reactants and products in them. Stoichiometry is a combination of mathematics and chemistry, and is applied based on one simple principle above, that matter never increases or decreases in a reaction. The first step to solving any chemistry problem is to balance the equations.
Step
Part 1 of 4: Balancing Chemical Equations

Step 1. Write down the number of atoms that make up each compound on both sides of the equation
Chemical equations can help you identify the atoms of each element in a reaction. In a chemical reaction, matter can neither be created nor destroyed, so an equation is said to be unequal if the number (and types) of constituent atoms on both sides of the equation are not exactly the same.
- Don't forget to multiply the number of atoms by the coefficient or the number below the line if you have one.
- For example, H2SO4 + Fe - Fe2(SO4)3 + H2
- On the left (reactants) side of the equation there are 2 H, 1 S, 4 O, and 1 Fe.
- On the right (product) side of the equation there are 2 H, 3 S, 12 O, and 2 Fe.
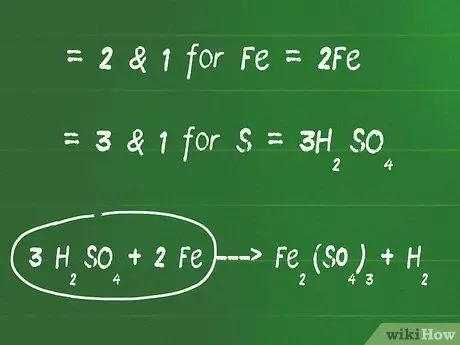
Step 2. Add coefficients in front of elements other than oxygen and hydrogen to balance both sides of the equation
Find the least common multiple of elements other than oxygen and hydrogen to equalize the number of atoms on both sides of the equation.
- For example, the least common multiple (LCM) between 2 and 1 is 2 for Fe. So, add the number 2 in front of the Fe element on the left side to balance it out.
- The LCM between 3 and 1 is 3 for the element S. So, add the number 3 in front of the compound H2SO4 to balance the right and left sides of the equation.
- At this stage, the equation of the example above will be: 3 H2SO4 + 2 Fe - Fe2(SO4)3 + H2

Step 3. Balance the hydrogen and oxygen atoms
The number of hydrogen and oxygen atoms is balanced last because they are generally present in several molecules on both sides of the equation. In the balancing step of this equation, don't forget to recalculate the atoms after you've added the coefficients in front of the molecules.
- In the example here, we add the number 3 in front of the compound H2SO4, so now there are 6 hydrogen atoms on the left side, but only 2 hydrogen atoms on the right side of the equation. We also currently have 12 oxygen atoms on the left side and 12 oxygen atoms on the right side, so the oxygen atoms are equivalent.
- We can balance the hydrogen atoms by adding the number 3 in front of H2.
- The final equation after balancing is 3 H2SO4 + 2 Fe - Fe2(SO4)3 + 3 H2.

Step 4. Recount the atoms on both sides of the equation to make sure they are the same number
Once done, recalculate and double check the equality is the right step. You can do this by adding up all the atoms on both sides of the equation and making sure they are the same.
- Check the equality of our equation again, 3 H2SO4 + 2 Fe - Fe2(SO4)3 + 3 H2.
- On the left side of the arrow are 6 H, 3 S, 12 O, and 2 Fe.
- On the right side of the arrow are 2 Fe, 3 S, 12 O, and 6 H.
- The number of atoms on the right and left sides is exactly the same, so this equation is already equivalent.
Part 2 of 4: Converting Grams and Mol
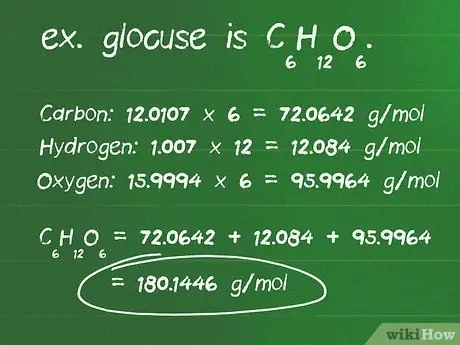
Step 1. Calculate the molar mass of the mass of the given compound in grams
Molar mass is the number of grams (g) in one mole of a compound. This unit allows you to easily convert grams and moles of a compound. To calculate the molar mass, you need to know how many molecules of the element are in the compound, as well as the atomic mass of each element in the compound.
- Find the number of atoms of each element in a compound. For example, glucose is C6H12O6, and is composed of 6 carbon atoms, 12 hydrogen atoms, and 6 oxygen atoms.
- Find out the atomic mass in grams per mole (g/mol) of each atom. The atomic masses of the elements that make up glucose are: carbon, 12.0107 g/mol; hydrogen, 1.007 g/mol; and oxygen, 15,9994 g/mol.
- Multiply each atom's mass by the number of atoms present in the compound. Carbon: 12.0107 x 6 = 72.0642 g/mol; hydrogen: 1.007 x 12 = 12,084 g/mol; oxygen: 15.9994 x 6 = 95.9964 g/mol.
- The sum of all the products above is the molar mass of the compound. 72, 0642 + 12, 084 + 95, 9964 = 180, 1446 g/mol. Or in other words, the mass of one glucose molecule is 180.14 grams.
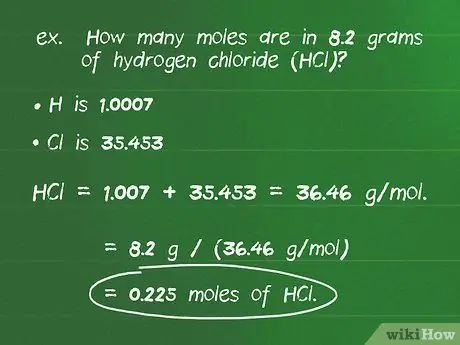
Step 2. Convert the mass of a compound to moles using the molar mass
Molar mass can be used as a conversion factor, so you can calculate the number of moles in a given number of grams of sample. Divide the known mass (g) by the molar mass (g/mol). An easy way to check your calculations is to make sure the units cancel each other out and leave only the moles.
- For example: how many moles are there in 8.2 grams of hydrogen chloride (HCl)?
- The atomic mass of H is 1.0007 and Cl is 35.453 so the molar mass of the above compound is 1.007 + 35.453 = 36.46 g/mol.
- Dividing the number of grams of the compound by its molar mass gives: 8.2 g / (36.46 g/mol) = 0.225 mol of HCl.

Step 3. Determine the molar ratio between the reactants
To determine the amount of product produced in a reaction, you must determine the molar ratio. The molar ratio is the ratio of the compounds reacting with each other, and is indicated by the coefficients of the compounds in the reaction that have been equivalent.
- For example, what is the molar ratio of KClO3 with O2 in the reaction of 2 KClO3 - 2 KCl + 3 O2.
- First of all, make sure that the above equations are equivalent. Never forget this step or the obtained molar ratio will be wrong. In this example, the amounts of each element on both sides of the equation are equal, so the reaction is balanced.
- The ratio between KClO3 with O2 is 2/3. You can put any number above and below, as long as it represents the appropriate compound throughout the problem solving.

Step 4. Multiply the cross by the molar ratio to find the number of moles of the other reactant
To calculate the number of moles of a compound produced or required in a reaction, you can use the molar ratio. Chemistry problems will usually ask you to determine the number of moles needed or produced in a reaction from the mass (grams) of a certain reactant.
- For example, in the reaction equation N2 + 3 H2 - 2 NH3 how many moles of NH3 which would result from 3.00 grams of N2 which reacts with H2 in sufficient quantity?
- In this example, H2 available in sufficient quantities and you do not have to count them to solve the problem.
- First, change the units of grams N2 be moles. The atomic mass of nitrogen is 14.0067 g/mol so the molar mass is N2 is 28.0134 g/mol. Division between mass and molar mass will give 3.00 g/28.0134 g/mol = 0.107 mol.
- Calculate the ratio in the problem: NH3: N2 = x/0, 107 moles.
- Cross multiply this ratio by the molar ratio of NH3 with N2: 2:1 x/0, 107 moles = 2/1 = (2 x 0, 107) = 1x = 0.214 moles.

Step 5. Convert this number of moles back to mass using the molar mass of the compound
You will use the molar mass again, but now the molar mass is needed as a multiplier to return the number of moles to grams. Be sure to use the correct molar mass of the compound.
Molar mass NH3 is 17.028 g/mol. So 0.214 moles x (17,028 grams/mol) = 3.647 grams of NH3.
Part 3 of 4: Converting Liters of Gas and Mol

Step 1. Find out if the reaction is taking place at standard pressure and temperature (STP)
STP is the set of conditions that allow 1 mole of an ideal gas to fill a volume of 22.414 liters (l). The standard temperature is 273, 15 Kelvin (K) and the standard pressure is 1 atmosphere (atm).
Generally, in problems it will be stated that the reaction takes place at 1 atm and 273 K, or in STP
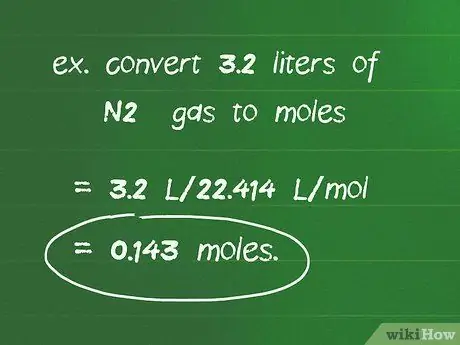
Step 2. Use the conversion factor of 22,414 l/mol to convert the number of liters of gas to moles of gas
If the reaction takes place under STP conditions, you can use 22.414 l/mol to calculate the number of moles in a known volume of gas. Divide the volume of gas (l) by this conversion factor to find the number of moles.
For example, to convert 3.2 liters of N2 gas to moles: 3.2 l/22, 414 l/mol = 0.143 mol.

Step 3. Use the ideal gas law to convert liters of gas if not under STP conditions
If the reaction in the problem does not take place under STP conditions, you must use the ideal gas law PV = nRT to calculate the number of moles in a reaction. P is the pressure in atmospheric units, V is the volume in liters, n is the number of moles, R is the gas law constant, 0.0821 l-atm/mol-degrees, and T is the temperature in degrees Kelvin.
- This equation can be rearranged to calculate moles, to become: n = RT/PV.
- The units of the gas constant are designed to eliminate all other unit variables.
- For example, determine the number of moles in 2.4 liters of O2 at 300 K and 1.5 atm. Plugging the variables into the equation, we get: n = (0.0821 x 300)/(1, 5 x 2) = 24, 63/3, 6 = 6, 842 moles O2.
Part 4 of 4: Converting Liters of Liquids and Mol
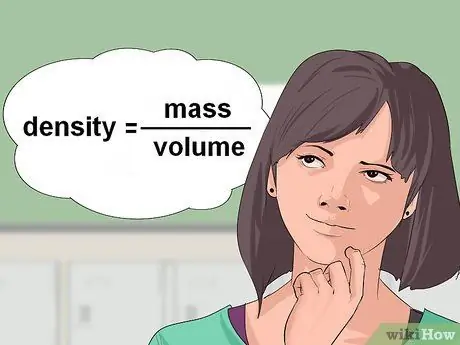
Step 1. Calculate the density of the liquid
Sometimes, chemical equations give you the volume of liquid reactant and ask you to calculate the number of grams or moles required for the reaction. To convert the volume of a liquid to grams, you need the density of the liquid. Density is expressed in units of mass/volume.
If the density is unknown in the problem, you may have to look it up in a textbook or on the internet

Step 2. Convert the volume to milliliters (ml)
To convert the volume of a liquid to mass (g), you must use its density. Density is expressed in grams per milliliter (g/ml), so the volume of a liquid must also be expressed in milliliters to calculate it.
Find out the known volume. For example, let's say in the problem that the volume of H. is known2O is 1 liter. To convert it to ml, you just need to multiply it by 1000 because there are 1000 ml in 1 liter of water.

Step 3. Multiply the volume by the density
When multiplying the volume (ml) by its density (g/ml), the ml unit is lost and what remains is the number of grams of the compound.
For example, the density H2O is 18.0134 g/ml. If the chemical equation says there are 500 ml of H2O, the number of grams in the compound is 500 ml x 18.0134 g/ml or 9006, 7 g.

Step 4. Calculate the molar mass of the reactants
Molar mass is the number of grams (g) in one mole of a compound. This unit allows you to change the units of grams and moles in a compound. To calculate the molar mass, you must determine how many molecules of the element are in a compound, as well as the atomic mass of each element in the compound.
- Determine the number of atoms of each element in a compound. For example, glucose is C6H12O6, and is composed of 6 carbon atoms, 12 hydrogen atoms, and 6 oxygen atoms.
- Find out the atomic mass in grams per mole (g/mol) of each atom. The atomic masses of the elements in glucose are: carbon, 12.0107 g/mol; hydrogen, 1.007 g/mol; and oxygen, 15,9994 g/mol.
- Multiply the atomic mass of each element by the number of atoms present in the compound. Carbon: 12.0107 x 6 = 72.0642 g/mol; hydrogen: 1.007 x 12 = 12,084 g/mol; oxygen: 15.9994 x 6 = 95.9964 g/mol.
- Add the multiplication results above to get the molar mass of the compound, which is 72, 0642 + 12, 084 + 95, 9964 = 180, 1446 g/mol. So, the mass of one mole of glucose is 180.14 grams.

Step 5. Convert the number of grams of a compound into moles using the molar mass
Using molar mass as a conversion factor, you can calculate the number of moles present in a given number of grams of sample. Divide the number of grams (g) of the known compound by the molar mass (g/mol). An easy way to check your calculations is to make sure the units cancel each other out and leave only the moles.
- For example: how many moles are there in 8.2 grams of hydrogen chloride (HCl)?
- The atomic mass of H is 1.0007 and Cl is 35.453 so the molar mass of the compound is 1.007 + 35.453 = 36.46 g/mol.
- Dividing the number of grams of the compound by the molar mass gives: 8.2 g/(36.46 g/mol) = 0.225 mol HCl.






