- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
The Z-score is used to take a sample in a data set or to determine how many standard deviations are above or below the mean.. To find the Z-score of a sample, you must first find its mean, variance, and standard deviation. To calculate the Z-score, you must find the difference between the sample value and the mean value, and then divide by the standard deviation. While there are many ways to calculate the Z-score from start to finish, this one is quite simple.
Step
Part 1 of 4: Calculating the Mean

Step 1. Pay attention to your data
You need some key information to calculate the mean or mean of your sample.
-
Know how much is in your sample. Take this sample of coconut trees, there are 5 coconut trees in the sample.

Calculate Z Scores Step 1Bullet1 -
Know the value shown. In this example, the value shown is the height of the tree.

Calculate Z Scores Step 1Bullet2 -
Pay attention to the variation in values. Is it in a large range, or a small range?

Calculate Z Scores Step 1Bullet3

Step 2. Collect all your data
You will need all those numbers to start the calculation.
- The mean is the average number in your sample.
- To calculate it, add up all the numbers in your sample, then divide by the sample size.
- In mathematical notation, n is the sample size. In the case of this sample tree height, n=5 because the number of trees in this sample is 5.
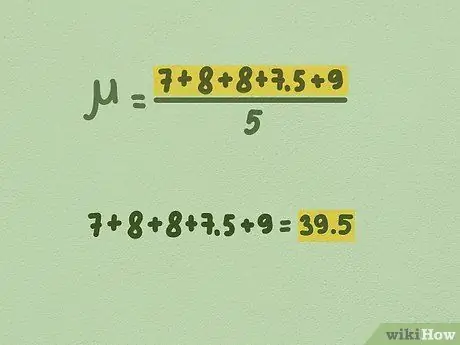
Step 3. Add up all the numbers in your sample
This is the first part of calculating the average or mean.
- For example, using a sample of 5 coconut trees, our sample consists of 7, 8, 8, 7, 5, and 9.
- 7 + 8 + 8 + 7, 5 + 9 = 39, 5. This is the total number of values in your sample.
- Check your answers to make sure you're adding up correctly.

Step 4. Divide the sum by your sample size (n)
This will return the average or mean of your data.
- For example, using our sample tree heights: 7, 8, 8, 7, 5, and 9. There are 5 trees in the sample, so n = 5.
- The sum of all the tree heights in our sample is 39. 5. Then this number is divided by 5 to get the mean.
- 39, 5/5 = 7, 9.
- The average tree height is 7.9 feet. The mean is usually denoted by the symbol, so = 7, 9
Part 2 of 4: Finding the Variance
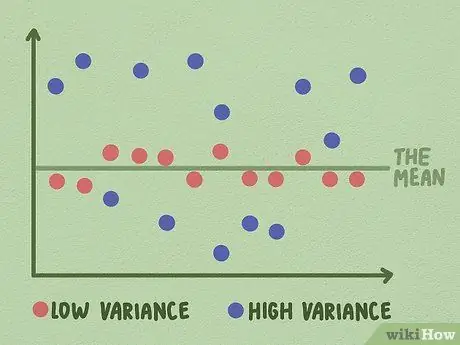
Step 1. Find the variance
The variance is a number that shows how far your data spreads from the mean.
- This calculation will tell you how far your data is spread out.
- Samples with low variance have data that cluster very closely around the mean.
- A sample with a high variance has data that is spread far from the mean.
- Variance is usually used to compare distributions between two data sets or samples.
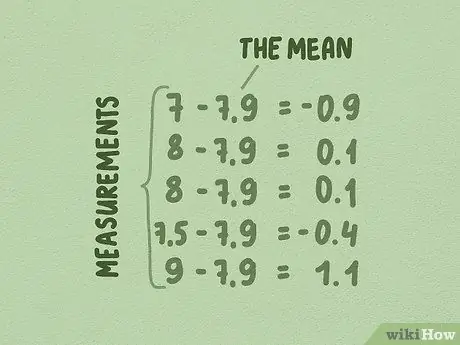
Step 2. Subtract the mean from each number in your sample
You'll find out how much each number in your sample differs from the mean.
- In our sample of tree heights, (7, 8, 8, 7, 5, and 9 feet) the mean is 7.9.
- 7 - 7, 9 = -0, 9, 8 - 7, 9 = 0, 1, 8 - 7, 9 = 0, 1, 7, 5 - 7, 9 = -0, 4, and 9 - 7, 9 = 1, 1.
- Repeat this calculation to make sure it is correct. It is very important that you get the values right in this step.
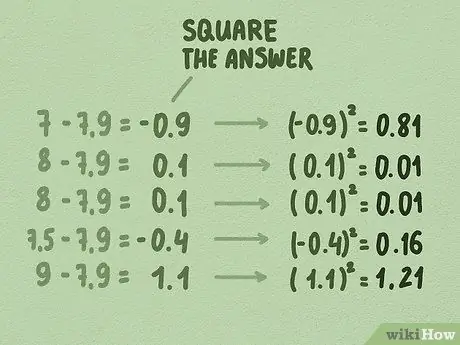
Step 3. Square all the numbers from the result of the subtraction
You will need each of these numbers to calculate the variance in your sample.
- Remember, in our sample, we subtract the mean of 7.9 with each of our data values. (7, 8, 8, 7, 5, and 9) and the results are: -0, 9, 0, 1, 0, 1, -0, 4, and 1, 1.
- Square all these numbers: (-0, 9)^2 = 0, 81, (0, 1)^2 = 0, 01, (0, 1)^2 = 0, 01, (-0, 4) ^2 = 0, 16, and (1, 1)^2 = 1, 21.
- The squared results of this calculation are: 0, 81, 0, 01, 0, 01, 0, 16, and 1, 21.
- Double-check your answers before moving on to the next step.
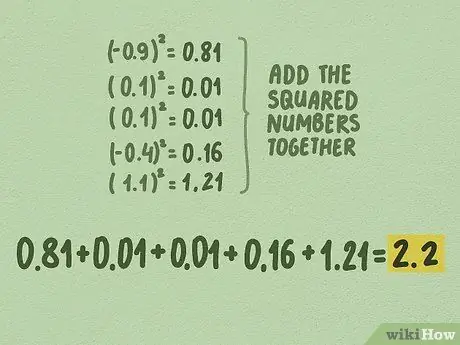
Step 4. Add up all the numbers that have been squared
This calculation is called the sum of the squares.
- In our sample tree height, the squared results are: 0, 81, 0, 01, 0, 01, 0, 16, and 1, 21.
- 0, 81 + 0, 01 + 0, 01 + 0, 16 + 1, 21 = 2, 2
- In our tree height example, the sum of the squares is 2, 2.
- Check your sum results to make sure your answer is correct before moving on to the next step.

Step 5. Divide the sum of the squares by (n-1)
Remember, n is your sample size (how many counts are in your sample). This step will generate the variance.
- In our sample of tree heights (7, 8, 8, 7, 5, and 9 feet), the sum of the squares is 2, 2.
- There are 5 trees in this sample. Then n = 5.
- n - 1 = 4
- Remember, the sum of the squares is 2, 2. to get the variance, calculate: 2, 2 / 4.
- 2, 2 / 4 = 0, 55
- Thus, the variance for this sample tree height is 0.55.
Part 3 of 4: Calculating the Standard Deviation
Step 1. Find the variance value
You need it to find the standard deviation of your sample.
- The variance is how far your data spreads from the mean or average.
- The standard deviation is a number that indicates how far the data in your sample is spread out.
- In our tree height sample, the variance is 0.55.

Step 2. Calculate the square root of the variance
This figure is the standard deviation.
- In our tree height sample, the variance is 0.55.
- 0, 55 = 0, 741619848709566. Usually a large decimal number will be obtained in this calculation. You may round up to two or three digits after the comma for your standard deviation value. In this case, we take 0.74.
- By rounding, our sample tree height sample standard deviation is 0.74

Step 3. Recheck the mean, variance, and standard deviation
This is to make sure you get the correct value for the standard deviation.
- Record all the steps you take while calculating.
- This allows you to see where you went wrong, if any.
- If you find different values of mean, variance, and standard deviation when checking, repeat the calculation and pay close attention to each process.
Part 4 of 4: Calculating Z Score
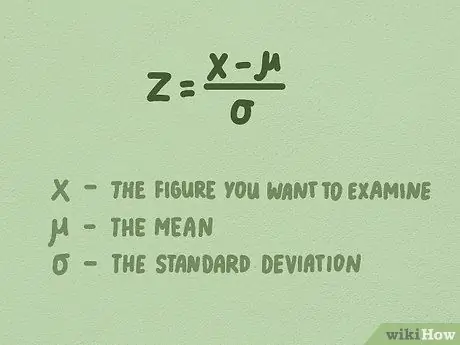
Step 1. Use this format to find the z-score:
z = X - /. This formula allows you to calculate a z-score for each data point in your sample.
- Remember, z-sore is a measure of how far the standard deviation is from the mean.
- In this formula, X is the number you want to test. For example, suppose you want to find how far the standard deviation is 7.5 from the mean in our tree height example, substitute X with 7.5
- While is the mean. In our sample of tree heights, the mean is 7.9.
- And is the standard deviation. In our sample tree height, the standard deviation is 0.74.
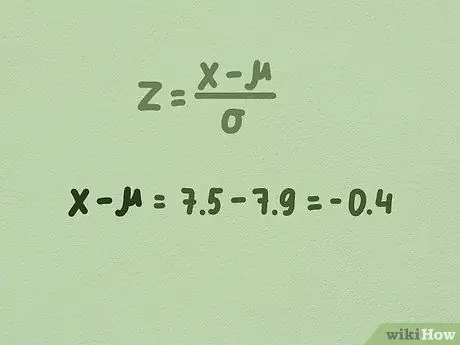
Step 2. Start the calculation by subtracting the mean from the data points you want to test
This will start the calculation of the z-score.
- For example, in our sample tree height, we want to find what the standard deviation is 7.5 from the mean 7.9.
- Then you would count: 7, 5 - 7, 9.
- 7, 5 - 7, 9 = -0, 4.
- Double-check until you find the correct mean and subtraction before continuing.
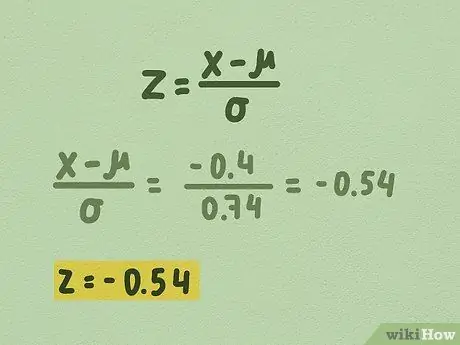
Step 3. Divide the result of the subtraction by the standard deviation
This calculation will return a z-score.
- In our sample tree height, we want the z-score of the data points of 7.5.
- We've subtracted the mean from 7.5, and come up with -0, 4.
- Remember, the standard deviation of our sample tree height is 0.74.
- - 0, 4 / 0, 74 = - 0, 54
- So, the z-score in this case is -0.54.
- This Z-score means this 7.5 is as far as -0.54 standard deviation from the mean in our sample tree height.
- The Z-score can be a positive or negative number.
- A negative z-score indicates that the data points are smaller than the mean, while a positive z-score indicates that the data points are larger than the mean.






