- Author Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
How to calculate power in horsepower or watts, what these terms mean, and why these terms are important.
Step
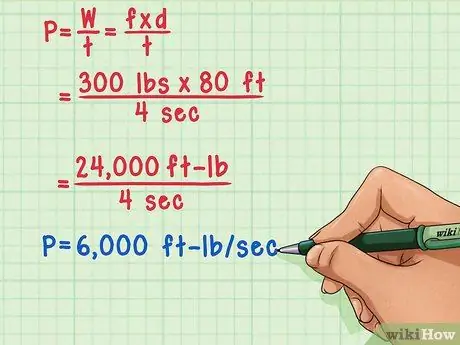
Step 1. Review the basics
The word power is defined as the time interval for doing work. Meanwhile, work is an old term for measuring how effective an applied force is in moving an inert object or facing an obstacle or other obstacle and covering a distance.
- The point here is that in order to do "work," a force must travel a distance. For example, if a propeller with a force of 300 N moves a ship in water 80 m, then the work done is FORCE x DISTANCE = 300 x 80 = 24,000 "Nm/Joule" --- so it can be said that the propeller the propeller has done 24,000 Joules of work.
- Consider the time it will take to move the ship that distance. Assume the ship is traveling this distance at a speed of 20 m per second (m/s). To cover a distance of 80 m, the ship takes 80/20 = 4 seconds. So, the ship's propeller does 24,000 Joules of work in 4 seconds, so power is applied at a rate of 24,000/4 = 6,000 Joules per second (J/s).
-
Understand the historical background of the timing. Back in the days before gasoline engines and steam power were used to power the first trains and ships (the first ship to use a propeller was HMS Britain whose first voyage took place in 1846 and used one propeller with 6 blades, which looks like a windmill), the horses do a very strenuous and varied job. Uniquely, people measure how much effort a horse can do and calculate the time. After searching for the average of a number of trials, they decided on 746 J/s as the standard rate of work done by a healthy horse. Later this standard became known as "horsepower". 746 Joules per second into one horsepower (hp). This is still true today.
746 X 60 = 44,760 Joules per minute, which is equal to: one hp
- Another universal unit of power, now generally limited to electronic and electrical equipment and based on the MKS (meter-kilogram-second/second) metric system, is the "watt". If one Newton of force travels a distance of one meter, then one joule of work has been done; if the force takes one second to do one joule of this work, then the power consumption is one watt. So one watt is one joule per second.
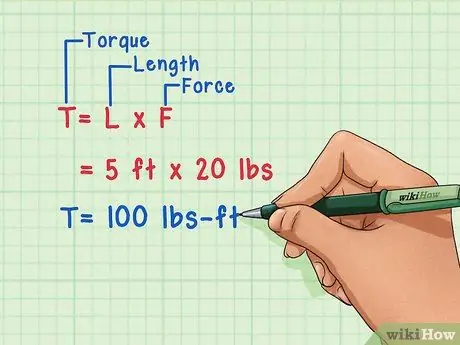
Step 2. Consider the industry in need at this time
In most cases in industry, we work with rotating machines and not machines with a straight motion like a horse plowing with a harrow on 160,000 m² of land. So, we should be able to determine the output power of things like electric motors, steam engines, turbines, diesels, etc., and thus, we get to know the subject of torque.
- Torque is a measurement of the tendency to change direction or rotate something or give rotational motion to an object on some axes. If you press the handle of a five-meter lever with a force of 20 Newtons, you are applying a torque of 5 X 20 = Newton-meters.
- Now, here's the difficulty and can lead to confusion. To calculate linear work on a straight line, you multiply the force by the displacement. Again, you are multiplying the force in the same units as the displacement, but in this case the displacement is the "lever arm" and even though you are producing torque, unless something is rotating, there is no movement and thus, no work.
- Work and torque, although they seem to be measured in the same unit, are actually very different. No work is done before the torque produces actual rotation, and thus, no power is used.
- Work is measured in Joules (J) while torque is measured in Newton.meters (Nm) to differentiate between the two.
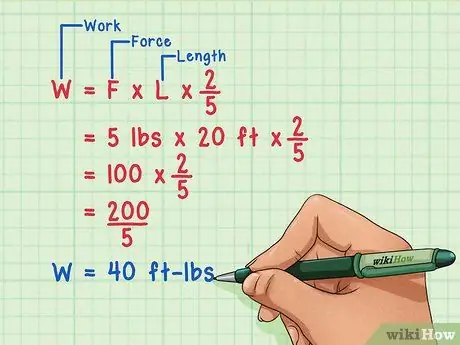
Step 3. Measure the work if there is any movement or rotational "displacement"
Suppose a lever is firmly locked at its fulcrum which ends in an axle and your hand, applying 20 N of force as before, travels a distance of two meters along the circle represented by the five meter lever, then work is done, as in the case of a straight line in above, equal to force times displacement or 20 X 2 = 40 Newton meters. Suppose you are simultaneously multiplying and dividing this number by the 5 meter long lever or "lever arm". Obviously, this won't change the result, so you can write:
- Work = 5 X 20 X 2/5 and the result is 40 Joules as before, but is 5 X 20 above that? You just saw that it is torque.
- What is "2/5"? The linear displacement of 2 meters divided by the lever arm, tells you how far you turned the axle in angular units called radians. A radian, used universally in physics and mechanical engineering, is defined as the angle between two radii of a circle such that the points on the circumference of a circle where the two radii intersect, are separated by the length of the radii of the circle. This calculation is very close to 57 degrees or is also the angle formed at the center of the circle by an arc that is equal to the radius of the circle at the circumference of the circle.
-
So you can say that the work done by a torque that produces a rotational displacement (theta) radians is equal to the torque (L)
- times the rotational displacement or
- work = L X theta in joules
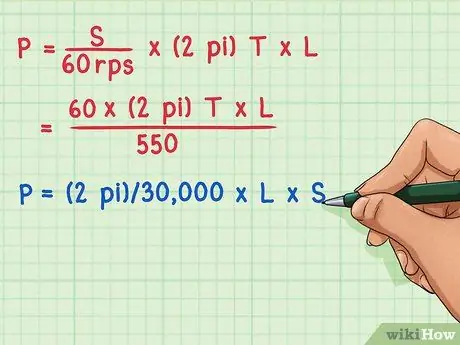
Step 4. Notice that you are much more interested in the amount of horsepower in the rotation of the motor and engine, i.e. the time interval for doing the rotational work:
- rotational power = torque X angular displacement (radians)/time (seconds)
-
In physics, angular velocity is written in radians per second, but any motor or airplane or ship engine you see is always measured in r.p.m (revolutions per minute), so we have to change that.
- One revolution per minute (rpm) = 60 revolutions/second = 60 rps, but one revolution per second = 2 X pi radians per second
- So the power in Joules per second of a rotating apparatus, producing a torque, L, and rotating at a speed S rpm, is
- Power = S/60 X (2 pi) X L in J/s and as previously written, to convert it to horsepower, you must divide by 746 or
- Motor horsepower = (2 pi)/44.760 X L X S where L is the torque measured in Newton meters (usually with a Prony brake) and S is the rotational speed in r.p.m which can be measured with a counter, stroboscope, laser, etc. In this way, the performance curves of car and motorcycle engines can be graphed in the form of a graph of torque versus r.p.m. and power (hp) versus engine speed in r.p.m. and automotive technicians can see its optimal performance from these charts.






