How to Calculate Standard Deviation: 12 Steps (with Pictures)

2024 Author: Jason Gerald | [email protected]. Last modified: 2023-12-16 10:50

The standard deviation describes the distribution of numbers in your sample. To determine this value in your sample or data, you need to do some calculations first. You need to find the mean and variance of your data before you can determine the standard deviation. The variance is a measure of how varied your data is around the mean.. The standard deviation can be found by taking the square root of your sample variance. This article will show you how to determine the mean, variance, and standard deviation.

Step

Part 1 of 3: Determining the Mean

Step 1. Pay attention to the data you have

This step is a very important step in any statistical calculation, even if it's just to determine simple numbers like the mean and median.

• Find out how many numbers are in your sample.
• Is the range of numbers in the sample very large? Or is the difference between each number small enough, like a decimal number?
• Know what data types you have. What does each number in your sample represent? This number can be in the form of test scores, heart rate readings, height, weight, and others.
• For example, a series of test scores are 10, 8, 10, 8, 8, and 4.

Step 2. Collect all your data

You need each number in your sample to calculate the mean.

• The mean is the average value of all your data.
• This value is calculated by adding up all the numbers in your sample, then dividing this value by how many there are in your sample (n).
• In the example test scores above (10, 8, 10, 8, 8, 4) there are 6 numbers in the sample. Thus, n = 6.

Step 3. Add all the numbers in your sample together

This step is the first part of calculating the mathematical average or mean.

• For example, use the test score data series: 10, 8, 10, 8, 8, and 4.
• 10 + 8 + 10 + 8 + 8 + 4 = 48. This value is the sum of all the numbers in the data set or sample.
• Re-sum all data to check your answer.

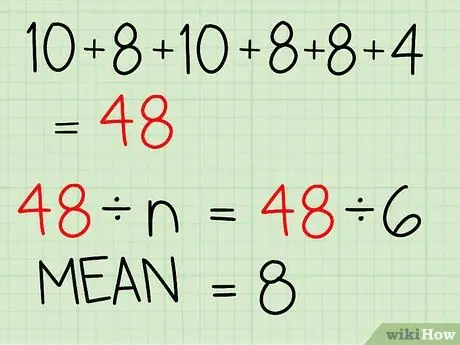
Step 4. Divide the number by how many numbers are in your sample (n)

This calculation will give the average or mean value of the data.

• In the sample test scores (10, 8, 10, 8, 8, and 4) there are six numbers, so, n = 6.
• The sum of the test scores in the example is 48. So you have to divide 48 by n to determine the mean.
• 48 / 6 = 8
• The mean test score in the sample is 8.

Part 2 of 3: Determining the Variance in the Sample

Step 1. Determine the variant

The variance is a number that describes how much your sample data clusters around the mean.

• This value will give you an idea of how widely distributed your data is.
• Samples with low variance values have data that are clustered very close to the mean.
• Samples with a high value of variance have data that are far apart from the mean.
• Variance is often used to compare the distribution of two data sets.

Step 2. Subtract the mean from each number in your sample

This will give you the value of the difference between each data item in the sample from the mean.

• For example, in the test scores (10, 8, 10, 8, 8, and 4) the mathematical mean or average value is 8.
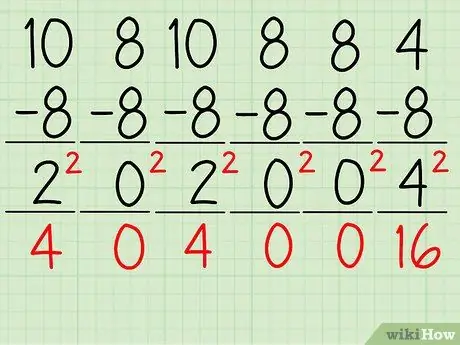
• 10 - 8 = 2; 8 - 8 = 0, 10 - 8 = 2, 8 - 8 = 0, 8 - 8 = 0, and 4 - 8 = -4.
• Do this one more time to check your answer. Making sure your answer is correct for each subtraction step is important because you will need it for the next step.

Step 3. Square all the numbers from each subtraction you just completed

You need each of these numbers to determine the variance in your sample.

• Remember, in the sample, we subtract each number in the sample (10, 8, 10, 8, 8, and 4) by the mean (8) and get the following values: 2, 0, 2, 0, 0 and - 4.
• To perform further calculations in determining the variance, you must perform the following calculations: 2², 0², 2², 0², 0², and (-4)² = 4, 0, 4, 0, 0, and 16.
• Check your answers before moving on to the next step.

Step 4. Add up the squared values to one

This value is called the sum of the squares.

• In the example of the test scores that we use, the squared values obtained are as follows: 4, 0, 4, 0, 0, and 16.
• Remember, in the test scores example, we started by subtracting each test score by the mean, and then squaring the result: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8- 8)^2 + (8-8)^2 + (4-8)^2
• 4 + 0 + 4 + 0 + 0 + 16 = 24.
• The sum of the squares is 24.

Step 5. Divide the sum of the squares by (n-1)

Remember, n is how many numbers are in your sample. Doing this step will give you the variance value.

• In the example test scores (10, 8, 10, 8, 8, and 4) there are 6 numbers. Thus n = 6.
• n-1 = 5.
• Remember the sum of the squares in this sample is 24.
• 24 / 5 = 4, 8
• Thus the variance of this sample is 4, 8.

Part 3 of 3: Calculating the Standard Deviation

Step 1. Determine the value of your sample variance

You need this value to determine the standard deviation of your sample.

• Remember, variance is how much the data spread from the mean or mathematical average value.
• The standard deviation is a value similar to the variance, which describes how the data is distributed in your sample.
• In the example of the test scores we are using, the variance values are 4, 8.

Step 2. Draw the square root of the variance

This value is the standard deviation value.

• Typically, at least 68% of all samples will fall within one standard deviation of the mean.
• Note that in the sample test scores, the variance is 4, 8.
• 4, 8 = 2, 19. The standard deviation in our sample test scores is therefore 2, 19.
• 5 of the 6 (83%) sample test scores we used (10, 8, 10, 8, 8, and 4) fell within the range of one standard deviation (2, 19) from the mean (8).

Step 3. Repeat the calculation to determine the mean, variance and standard deviation

You need to do this to confirm your answer.

• It is important to write down all the steps you take when calculating by hand or with a calculator.
• If you get a different result from your previous calculation, double-check your calculation.
• If you can't find where you went wrong, go back and compare your calculations.