- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
Adding fractions with different denominators may seem complicated, but once you get the denominators equal, you can add up the fractions easily. If you are working on a common fraction problem with a numerator that is greater than the denominator, make the denominators the same for the two fractions. After that, add up the two numerators. If you're adding mixed numbers, first convert the numbers to common fractions and equate the two fractions. This way, you can easily add the two fractions together.
Step
Method 1 of 2: Adding Common Fractions

Step 1. Find the least common multiple (LCM) for the denominator
Since you need to equalize both denominators before adding fractions, find the LCM of the denominators. After that, select the smallest LCM.
For example, for the problem 9/5 + 14/7, the multiples of 5 are 5, 10, 15, 20, 25, 30, and 35, while the multiples of 7 are 7, 14, 21, 28, and 35. The number 35 is the least common multiple of the two numbers
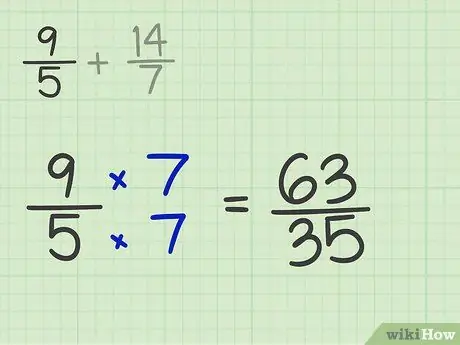
Step 2. Multiply the numerator and denominator to get the proper denominator
You need to multiply all the fractions so that the denominator is the least common multiple of the previous one.
For example, multiply 9/5 by 7 to get 35 as the denominator. Also multiply the numerator by 7. After that, the fraction will be 63/35

Step 3. Convert other fractions to equivalent fractions
Keep in mind that when you adjust the first fraction in a problem, you also need to adjust the other fractions so that they are equivalent.
For example, if you change 9/5 to 63/35, multiply 14/7 by 5 to get the fraction 70/35. The original 9/5 + 14/7 addition problem has now changed to 63/35 + 70/35
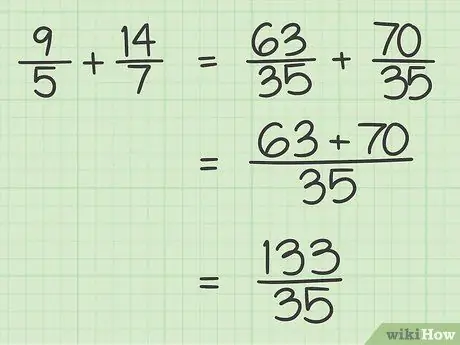
Step 4. Add the two numerators without changing the denominator
Once the denominators for both fractions are the same, add up the numerators. Place the answer above the denominator.
For example, 63 + 70 = 133. Write the sum over the denominator so you get 133/35
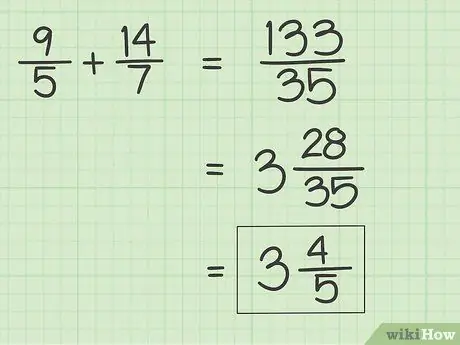
Step 5. Simplify or reduce answers if necessary
If the numerator is greater than the denominator (known as an improper fraction), convert the fraction to a mixed number. To change this, divide the numerator by the denominator until you get an integer. After that, check the remainder of the division and place the remainder above the denominator. Reduce the fraction if it can still be simplified.
For example, 133/35 can be simplified to 28/35. This fraction can also be reduced back to 4/5 so that the final answer to your addition problem is 3 4/5
Method 2 of 2: Adding Mixed Fractions
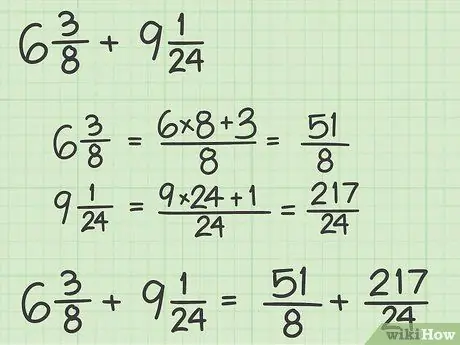
Step 1. Convert mixed fractions to improper fractions
If you get a fraction with a whole number, convert it to a common fraction to make it easier to add. The numerator of your fraction will be greater than the denominator.
For example, 6 3/8 + 9 1/24 can be converted to 51/8 + 217/24

Step 2. Find the least common multiple if necessary
If the denominators of the two fractions are different, you will need to write down multiples for each denominator so you can find a single multiple of the same number. For example, for 51/8 + 217/24, write down the multiples of 8 and 24 until you find 24.
Since multiples of 8 include 8, 16, 24, 32, and 48, and multiples of 24 include 24, 48, and 72, the number 24 can be chosen as the least common multiple

Step 3. Convert the fraction to an equivalent fraction if you need to change the denominator
All denominators must be converted to the least common multiple that you previously got. Multiply all fractions by a certain number to change the denominator to the least common multiple.
For example, to change the denominator from 51/8 to 24, multiply all fractions by 3. You will get the fraction 153/24 from the product
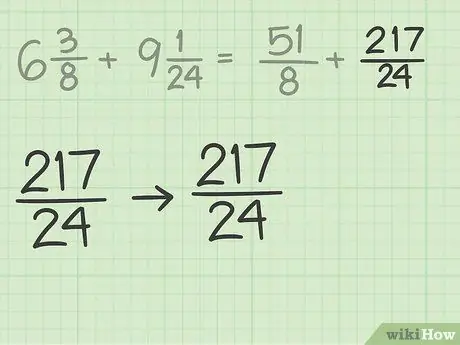
Step 4. Change all the fractions in the problem so that they are equivalent
If the denominators of the other fractions in the problem are different, you'll also need to multiply them so that they're the same as the denominators of the previous fraction. If you already have a common denominator, the fractions don't need to be adjusted.
For example, if you have the fraction 217/24, you don't need to adjust it because it already has the same denominator as the previous fraction
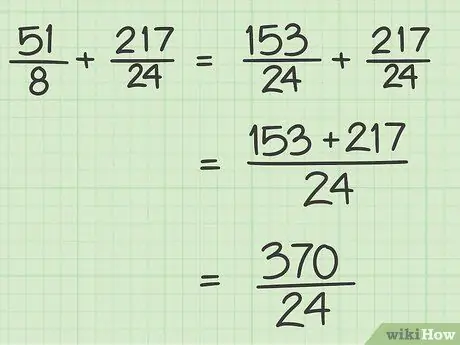
Step 5. Add the two numerators without changing the denominator
You can add the two numerators together after the denominators are equal (or if they have been the same since the beginning). After the two numerators have been added, write the answer above the denominator. Don't add the denominators of the two fractions.
For example, 153/24 +217/24 = 370/24
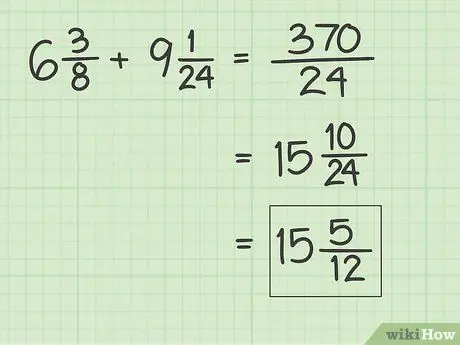
Step 6. Simplify the answer
If the numerator of the sum is greater than the denominator, you need to divide it until you get an integer. To get a mixed number, record the remainder of the division. After that, place the remainder of the division above the same denominator. Keep reducing the fraction until you get to the simplest form.






