How to Calculate the Voltage Through a Resistor (with Pictures)

2024 Author: Jason Gerald | [email protected]. Last modified: 2024-01-15 08:07

Before calculating the voltage across a resistor, you must first determine the type of circuit (strand) used. If you need to revisit basic terms or need help understanding electrical circuits, start with the first section. Otherwise, go directly to the type of circuit you want to work on

Step

Part 1 of 3: Understanding Electrical Circuits

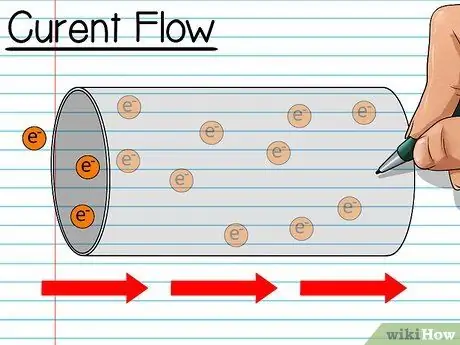
Step 1. Learn about electric current

You can use the following analogy: imagine that you are pouring cereal into a bowl. Each grain of grain is an electron, and the flow of grain into the bowl is an electric current. When you talk about electricity, you explain it by saying how many grains of cereal flow each second. When you talk about electric current, you measure it in units of ampere (amps), which is a certain number of electrons (which are very large values) that flow every second.

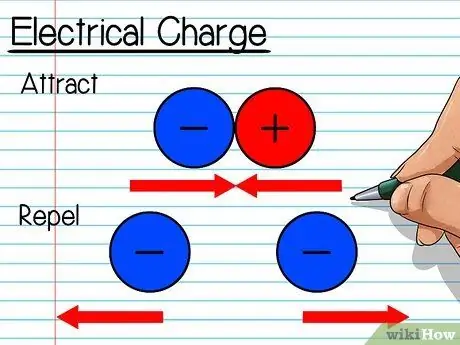
Step 2. Know about electric charge

Electrons have a "negative" electric charge. That is, electrons attract (or flow towards) positively charged objects, and repel (or flow away from) negatively charged objects. All electrons have a negative charge so they always push other electrons and scatter.

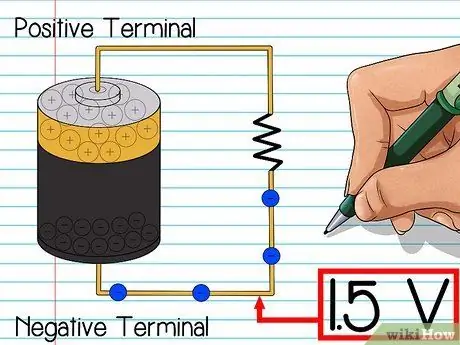
Step 3. Understand about voltage

Voltage measures the difference in electric charge between two points. The bigger the difference, the stronger the two points attract each other. Here's an example of using a regular battery:

• Inside the battery, the chemical reactions that occur produce a pool of electrons. These electrons go to the negative pole of the battery, while the positive pole remains almost empty. These are called the positive and negative terminals. The longer this process lasts, the greater the voltage between the two poles.
• When you connect the wires between the positive and negative poles, the electrons at the negative pole now have somewhere to go. The electrons at the negative pole flow towards the positive pole and produce an electric current. The greater the voltage, the more electrons move to the positive pole every second.

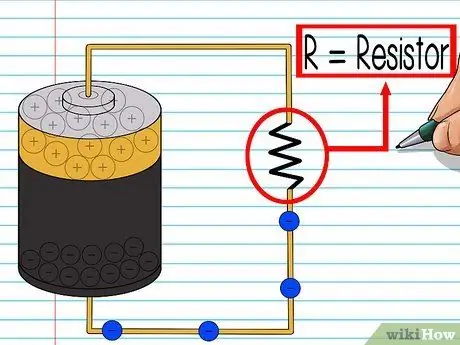
Step 4. Learn about resistance

An obstacle is something that blocks electrons. The greater the resistance, the harder it is for electrons to pass. The resistance slows the electric current because the number of electrons that pass each second decreases.

Resistors can be anything in an electrical circuit that adds resistance. You can buy real “resistors”, but in problems, resistors are usually represented by light bulbs or anything that has resistance

Step 5. Memorize Ohm's Law

There is a simple relationship between current, voltage and electrical resistance. Write or memorize the following formula as you will need it to solve problems related to electrical circuits:

• Current = voltage divided by resistance
• The formula can be written as follows: I = ^V / _R
• Think what happens if the V (voltage) or R (resistance) in the circuit increases. Is it in accordance with the discussion above?

Part 2 of 3: Calculating the Voltage Through a Resistor (Series Circuit)

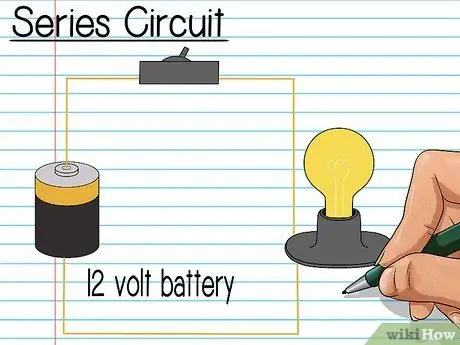
Step 1. Understand about series circuits

Series electrical circuits are very easy to spot. The shape is in the form of a cable loop with all components arranged in a row along the cable. An electric current flows through the entire wire and through every resistor or element it encounters.

• Electric current always the same at every point in the circuit.
• When calculating voltage, the location of the resistor in the circuit is irrelevant. You can take a resistor and move it across the circuit, and the voltage across each resistor remains the same.
• We will use an example of an electrical circuit with 3 resistors in series: R₁, R₂, and R₃. The circuit gets power from a 12 volt battery. We will find the voltage across each resistor.

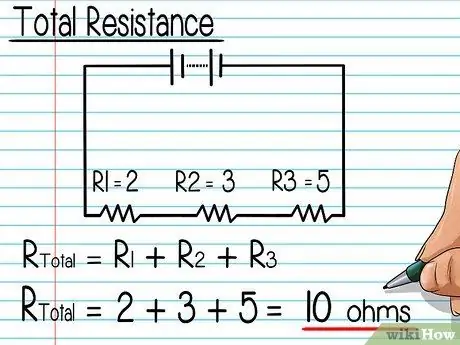
Step 2. Calculate the total resistance

Add up all the resistance values in the circuit. The result is the total resistance of the series circuit.

For example, the three resistors R₁, R₂, and R₃ have resistances of 2 (ohms), 3, and 5, respectively. Thus, the total resistance is 2 + 3 + 5 = 10 ohms.

Step 3. Find the current in the circuit

Use Ohm's Law to find the value of the current in an entire electrical circuit. Remember, in a series circuit, the current is always the same at every point of the circuit. Having obtained the current value, we can carry out all the remaining calculations.

Ohm's law states that current I = ^V / _R. The voltage across the circuit is 12 volts, and the total resistance of the circuit is 10 ohms. Plug these numbers into the formula to get I = ¹² / ₁₀ = 1.2 amperes.

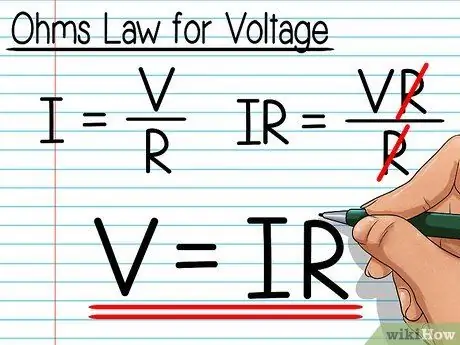
Step 4. Adjust Ohm's Law to find the voltage value

Use basic algebra to find the value of voltage instead of current:

• I = ^V / _R
• IR = ^VR / _R
• IR = V
• V = IR

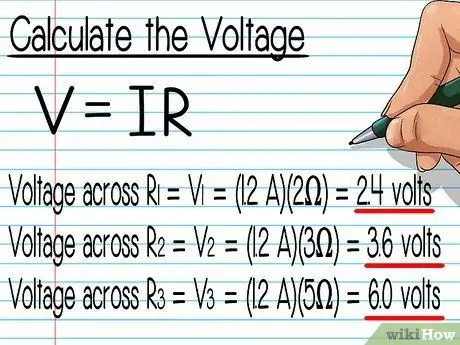
Step 5. Calculate the voltage across each resistor

We already know the value of resistance and current. Now, we can do all the calculations. Plug the numbers into the formula and complete the calculation. Here are the calculations for the three resistors from the example above:

• Voltage at R₁ = V₁ = (1, 2A)(2Ω) = 2, 4 volts.
• Voltage at R₂ = V₂ = (1, 2A)(3Ω) = 3.6 volts.
• Voltage at R₃ = V₃ = (1, 2A)(5Ω) = 6 volts.

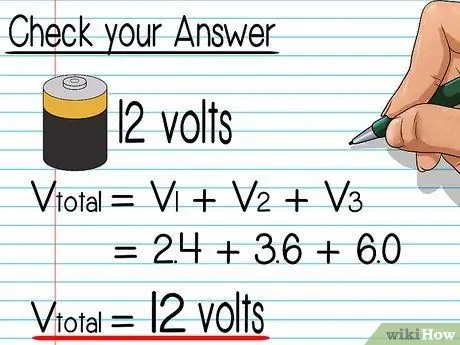
Step 6. Check your answers

In a series circuit, the sum of all the answers must equal the total voltage. Add up each voltage you calculated and check that it matches the total voltage of the circuit. If not, try to find the error in your calculations.

• According to the example above, 2, 4 + 3, 6 + 6 = 12 volts, equal to the total voltage through the electrical circuit.
• If your answer is a little off (say 11, 97 instead of 12), chances are you've rounded numbers while working on formulas. Don't worry, your answer is not wrong.
• Remember, voltage measures the difference in charge, or the number of electrons. Imagine that you are counting the new electrons seen as they travel along an electrical circuit. If you calculate correctly, you will know the total change in electrons from start to finish.

Part 3 of 3: Calculating the Voltage Through a Resistor (Parallel Circuit)

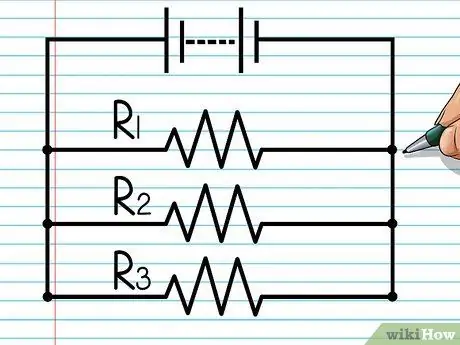
Step 1. Learn about parallel circuits

Imagine a cable connecting to one pole of the battery, then branching off into two separate wires. These two wires are parallel to each other, then reconnect before connecting to the other pole of the battery. If the wire on the left is connected to a resistor, and the wire on the right is also connected to another resistor, the two resistors are connected in "parallel".

You can add as many parallel cables as you like. This guide can be used for electrical circuits that branch into 100 wires which then reconnect

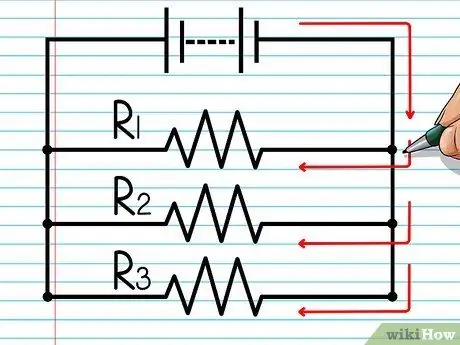
Step 2. Know how electric current flows in parallel circuits

Electric current flows through every available path. Electric current will flow through the wire on the left, through the resistor on the left, and all the way to the other end. At the same time, current also flows through the wire on the right, through the resistor on the right, and all the way to the end. No wires or resistors in a parallel circuit are passed through twice.

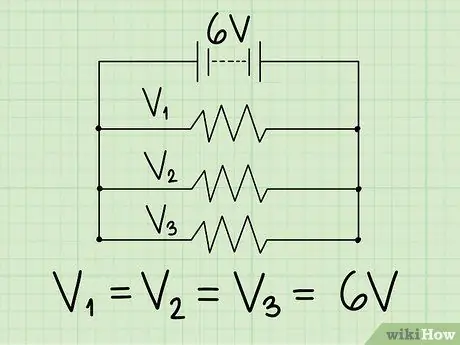
Step 3. Use the total voltage to find the voltage across each resistor

If you know the voltage across the entire circuit, the answer is easy to find. Each parallel wire has the same voltage as the entire electrical circuit. Say an electrical circuit has two resistors in parallel and a 6 volt battery. Barriers are not very relevant today. To understand it, recall the series circuit described above:

• Remember that the sum of the voltages in a series circuit is always equal to the total voltage through the electric circuit.
• Imagine each path that current takes in a series circuit. The same is true for parallel circuits: if you add up all the voltages, the result is equal to the total voltage.
• Since the current through each parallel wire is only through one resistor, the voltage across the resistor must equal the total voltage.

Step 4. Calculate the total current of the electric circuit

If the problem doesn't give the total voltage across the circuit, you'll need to complete a few additional steps. Start by finding the total current through the electric circuit. In a parallel circuit, the total current is equal to the sum of the currents through each parallel path.

• The formula is as follows: I_total = I₁ + I₂ + I₃…
• If you have trouble understanding it, imagine a water pipe that has two branches. The total amount of water flowing in a series of pipes is the sum of the water flowing in each pipe.

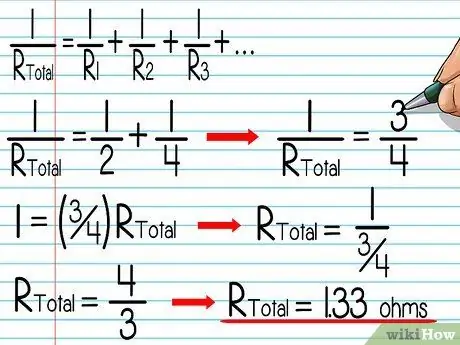
Step 5. Calculate the total resistance of the electric circuit

The effectiveness of a resistor is reduced in a parallel circuit because it only blocks the current through one wire. In fact, the more wires in a circuit, the easier it is for current to find a path to flow smoothly. To find the total resistance, find the value of R. _total in this equation:

• ¹ / _Rtotal = ¹ / _R1 + ¹ / _R2 + ¹ / _R3 …
• For example, an electrical circuit has resistors of 2 ohms and 4 ohms connected in parallel, respectively. ¹ / _Rtotal = 1/2 + 1/4 = 3/4 → 1 = (3/4)R_total → R_total = 1/(3/4) = 4/3 = ~1.33 ohms.

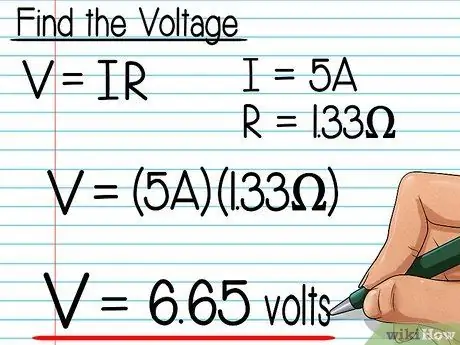
Step 6. Find the voltage from your answer

Remember, once we find the total voltage of the electric circuit, we already know the magnitude of the voltage through each parallel wire. Use Ohm's Law to complete the calculation. Take a look at the following example questions:

• The electric circuit has a current of 5 amperes and a total resistance of 1.33 ohms.
• According to Ohm's Law, I = V / R so that V = IR
• V = (5A)(1, 33Ω) = 6.65 volts.

Tips

• If you have a complicated electrical circuit, for example having resistors connected in parallel and series, select the two closest resistors. Find the total resistance through the two resistors using the rules for resistors in series and parallel circuits. Now, you can treat it as a single resistor. Continue this process until you have a circuit in which the resistors are arranged only in series or parallel.
• The voltage across the resistor is often called the "voltage drop."

• Understand the following terms:

  • Electrical circuit/strand – The arrangement of various components (resistors, capacitors, and inductors), which are connected by cables and can be energized.
  • Resistor – an element that reduces or inhibits electric current.
  • Current – The flow of electric charge in the cable. Expressed in Ampere (A).
  • Voltage – The amount of electric charge that passes each second. Expressed in units of volts (V).
  • Resistance – A measure of an element's opposition to electric current. Expressed in Ohms (Ω)