Deriving a polynomial function can help track changes in its slope. To derive a polynomial function, all you have to do is multiply the coefficients of each variable by their respective powers, decrease by one degree, and remove any constants. If you want to know how to break it down into a few easy steps, keep reading.
Step
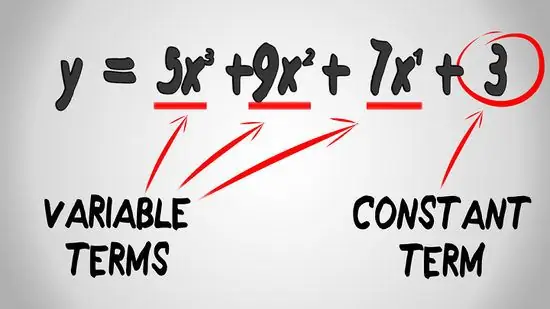
Step 1. Determine the terms of the variables and constants in the equation
A variable term is any term that has a variable and a constant term is any term that has only numbers without variables. Find the terms of the variables and constants in this polynomial function: y = 5x3 + 9x2 + 7x + 3
- The variable terms are 5x3, 9x2, and 7x.
- The constant term is 3.
Step 2. Multiply the coefficients of each variable term by their respective powers
The multiplication result will produce a new coefficient from the derived equation. Once you find the product of the product, place the product in front of the respective variable. Here's how you do it:
- 5x3 = 5 x 3 = 15
- 9x2 = 9 x 2 = 18
- 7x = 7 x 1 = 7
Step 3. Lower one level per rank
To do this, just subtract 1 from each power in each variable term. Here's how you do it:
- 5x3 = 5x2
- 9x2 = 9x1
- 7x = 7
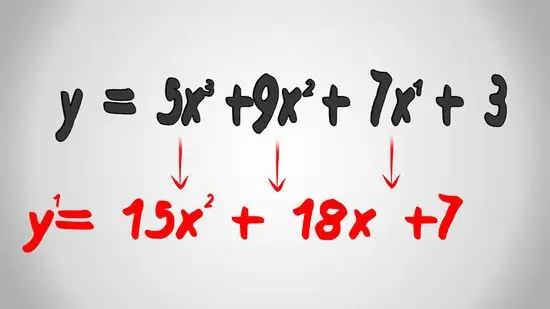
Step 4. Replace the old coefficients and powers with the new ones
To solve the derivation of this polynomial equation, replace the old coefficient with the new coefficient and replace the old exponent with a power that has been derived one level. The derivative of the constant is zero so you can omit 3, the constant term, from the final result.
- 5x3 be 15x2
- 9x2 be 18x
- 7x becomes 7
- The derivative of the polynomial y = 5x3 + 9x2 + 7x + 3 is y = 15x2 + 18x + 7
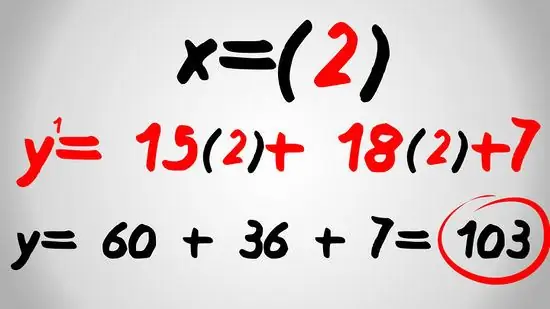
Step 5. Find the new equation value with the given "x" value
To find the value of "y" with the given value of "x", just replace all the "x" in the equation with the given value of "x" and solve. For example, if you want to find the value of the equation when x = 2, just enter the number 2 in each term of x in the equation. Here's how you do it:
- 2 y = 15x2 + 18x+ 7 = 15 x 22 + 18 x 2 + 7 =
- y = 60 + 36 + 7 = 103
- The value of the equation when x = 2 is 103.
Tips
- If you have negative exponents or fractions, don't worry! This rank also follows the same rules. If for example you have x-1, will be -x-2 and x1/3 be (1/3)x-2/3.
- This is called the Power Rule of Calculus. The contents are: d/dx[ax ]=naxn-1
- Finding the indeterminate integral of a polynomial is done the same way, only the other way around. Suppose you have 12x2 + 4x1 +5x0 + 0. So you just add 1 to each exponent and divide by the new exponent. The result is 4x3 + 2x2 + 5x1 + C, where C is a constant, because you can't know the magnitude of the constant.
- Remember that the definition of derivation is:: lim with h->0 of [f(x+h)-f(x)]/h
- Remember, this method only works if the exponent is a constant. For example, d/dx x^x is not x(x^(x-1))=x^x, but is x^x(1+ln(x)). The power rule only applies to x^n for the constant n.
