6 Ways to Factor Second Degree Polynomials (Square Equations)

2024 Author: Jason Gerald | [email protected]. Last modified: 2024-01-19 22:11

A polynomial contains a variable (x) with a power, known as a degree, and several terms and/or constants. To factor a polynomial means to break the equation into simpler equations that can be multiplied. This skill is in Algebra 1 and up, and may be difficult to grasp if your math skills are not at this level.

Step

Start

Step 1. Set up your equation

The standard format for a quadratic equation is:

ax² + bx + c = 0

Start by ordering the terms in your equation from highest to lowest power, just like in this standard format. For example:

6 + 6x² + 13x = 0

We'll reorder this equation so that it's easier to work with by simply moving the terms:

6x² + 13x + 6 = 0

Step 2. Find the form factor using one of the following methods

Factoring the polynomial results in two simpler equations that can be multiplied to produce the original polynomial:

6x² + 13x + 6 = (2x + 3)(3x + 2)

In this example, (2x + 3) and (3x + 2) are the factors of the original equation, 6x² +13x+6.

Step 3. Check your work

Multiply the factors you have. Then, combine like terms and you're done. Start with:

(2x + 3)(3x + 2)

Let's try, multiply the terms using PLDT (first – outside – inside – last), resulting in:

6x² + 4x + 9x + 6

From here, we can add up 4x and 9x because they are like terms. We know that our factors are correct because we get our original equation:

6x² + 13x + 6

Method 1 of 6: Trial and Error

If you have a fairly simple polynomial, you might be able to find the factors yourself just by looking at them. For example, after practice, many mathematicians can figure out that the equation 4x² + 4x + 1 has a factor of (2x + 1) and (2x + 1) just by looking at it often. (This of course will not be easy for more complicated polynomials). For this example, let's use a less frequently used equation:

3x² + 2x - 8

Step 1. Write a list of the factors of term a and term c

Using the ax equation format² + bx + c = 0, identify the terms a and c and write down the factors that both terms have. For 3x² + 2x - 8, meaning:

a = 3 and has a set of factors: 1 * 3

c = -8 and has four sets of factors: -2 * 4, -4 * 2, -8 * 1, and -1 * 8.

Step 2. Write down two sets of brackets with blank spaces

You'll fill in the blanks you've created with constants for each equation:

(x)(x)

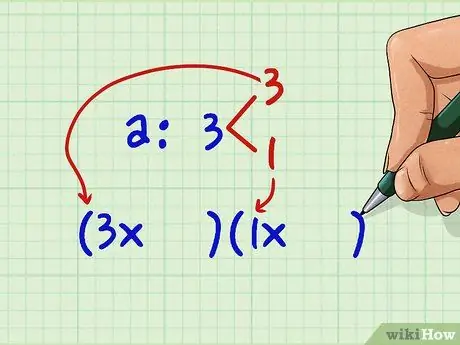
Step 3. Fill in the blanks in front of x with the possible pairs of factors for the value of a

For the term a in our example, 3x², there is only one possibility for our example:

(3x)(1x)

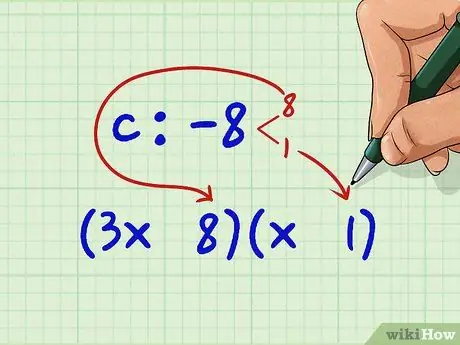
Step 4. Fill in the two blanks after x with pairs of factors for the constant

Suppose we choose 8 and 1. Write in them:

(3x

Step 8.)(

Step 1

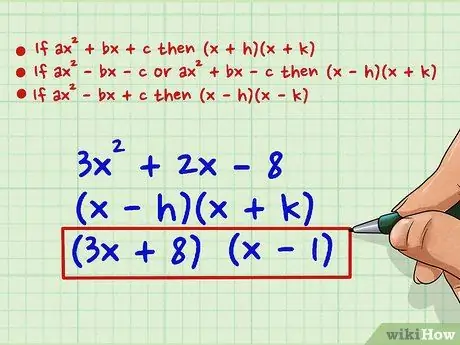
Step 5. Determine the sign (plus or minus) between the variable x and the number

Depending on the signs in the original equation, it may be possible to search for signs for constants. Suppose we call two constants h and k for our two factors:

If ax² + bx + c then (x + h)(x + k)

If ax² - bx - c or ax² + bx - c then (x - h)(x + k)

If ax² - bx + c then (x - h)(x - k)

For our example, 3x² + 2x - 8, the signs are:(x - h)(x + k), giving us two factors:

(3x + 8) and (x - 1)

Step 6. Test your choices using first-out-in-last multiplication (PLDT)

The first quick test is to see if the middle term has at least the correct value. If not, you may have chosen the wrong c factors. Let's test our answer:

(3x + 8)(x - 1)

By multiplication, we get:

3x² - 3x + 8x - 8

Simplifying this equation by adding the like terms (-3x) and (8x), we get:

3x² - 3x + 8x - 8 = 3x² + 5x - 8

Now we know that we must have used the wrong factors:

3x² + 5x - 8 3x² + 2x - 8

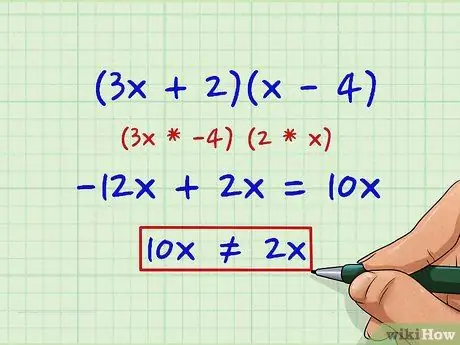
Step 7. Change your selection if needed

In our example, let's try 2 and 4 instead of 1 and 8:

(3x + 2)(x - 4)

Now our c term is -8, but our outside/inside product (3x * -4) and (2 * x) is -12x and 2x, which combined will not produce the correct b +2x term.

-12x + 2x = 10x

10x 2x

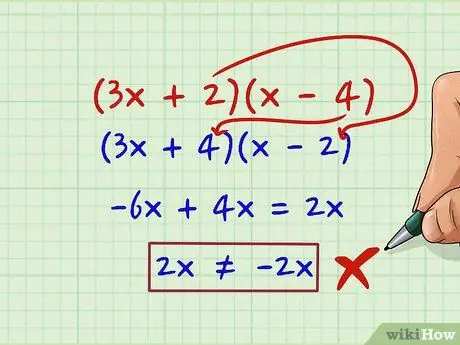
Step 8. Reverse the order if necessary

Let's try swapping 2 and 4:

(3x + 4)(x - 2)

Now, our c term (4 * 2 = 8) is correct, but the outer/inner product is -6x and 4x. If we combine them:

-6x + 4x = 2x

2x -2x We're pretty close to 2x we're looking for, but the sign is wrong.

Step 9. Double check your tags if needed

We'll use the same order, but swap out the equations that have the minus sign:

(3x - 4)(x + 2)

Now the term c is no problem, and the current outer/inner product is (6x) and (-4x). Because:

6x - 4x = 2x

2x = 2x Now we can use positive 2x from the original problem. These must be the correct factors.

Method 2 of 6: Decomposition

This method will identify all the possible factors of the terms a and c and use them to find the correct factors. If the numbers are too big or guessing seems time-consuming, use this method. Let's use an example:

6x² + 13x + 6

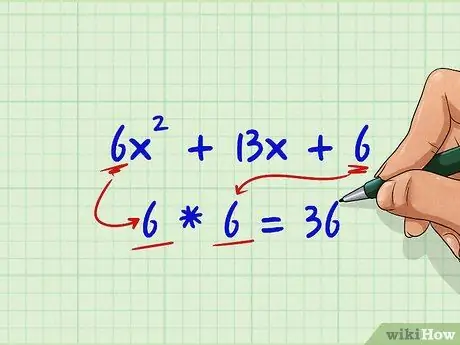
Step 1. Multiply term a by term c

In this example, a is 6 and c is also 6.

6 * 6 = 36

Step 2. Get the term b by factoring and testing

We are looking for two numbers that are factors of the product a * c that we have identified and also add up to the term b (13).

4 * 9 = 36

4 + 9 = 13

Step 3. Substitute the two numbers you get into your equation as the result of adding term b

Let's use k and h to represent the two numbers we have, 4 and 9:

ax² + kx + hx + c

6x² + 4x + 9x + 6

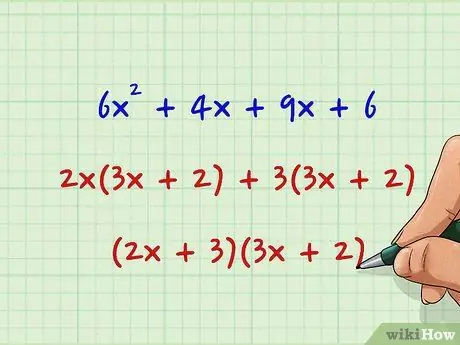
Step 4. Factor the polynomial by grouping

Arrange the equations so that you can take the greatest common factor of both the first and second terms. The group of factors must be the same. Add the Greatest Common Factor and place it in parentheses next to the factor group; the result is your two factors:

6x² + 4x + 9x + 6

2x(3x + 2) + 3(3x + 2)

(2x + 3)(3x + 2)

Method 3 of 6: Triple Play

Similar to the decomposition method, the triple play method examines the possible factors of multiplying the terms a and c and using the value of b. Try using this example equation:

8x² + 10x + 2

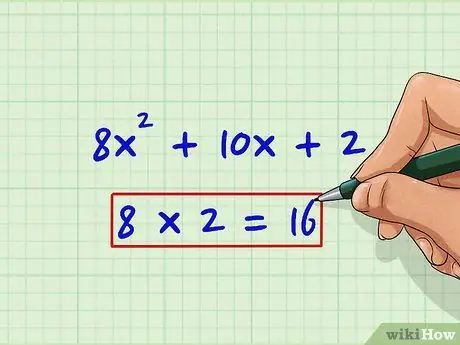
Step 1. Multiply term a by term c

Like the parsing method, this will help us identify candidates for term b. In this example, a is 8 and c is 2.

8 * 2 = 16

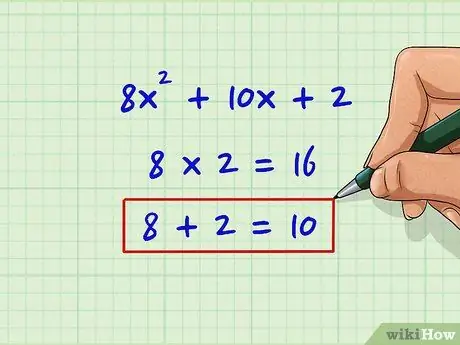
Step 2. Find two numbers which, when multiplied by numbers, give this number with a total sum equal to the term b

This step is the same as parsing – we test and discard candidates for the constant. The product of the terms a and c is 16, and the term c is 10:

2 * 8 = 16

8 + 2 = 10

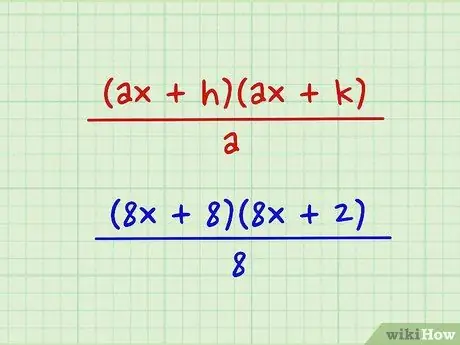
Step 3. Take these two numbers and test them by plugging them into the triple play formula

Take our two numbers from the previous step – let's call them h and k – and plug them into the equation:

((ax + h)(ax + k))/ a

We will get:

((8x + 8)(8x + 2)) / 8

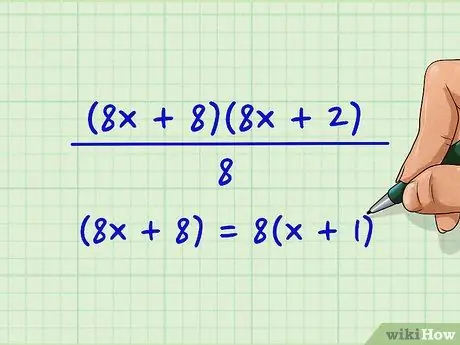
Step 4. Notice if any of the two terms in the numerator are divisible by a

In this example, we saw if (8x + 8) or (8x + 2) is divisible by 8. (8x + 8) is divisible by 8, so we'll divide this term by a and leave the other factors alone.

(8x + 8) = 8(x + 1)

The term in parentheses here is what's left after we divide by the term a.

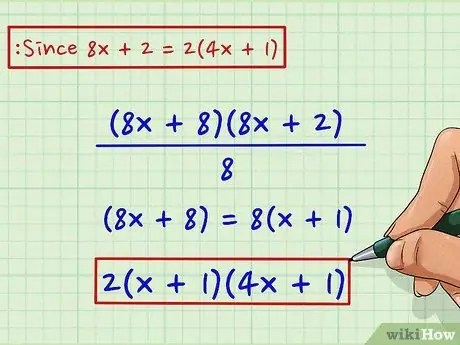
Step 5. Take the greatest common factor (GCF) of one or both terms, if any

In this example, the second term, has a GCF of 2, because 8x + 2 = 2(4x + 1). Combine this result with the term you got from the previous step. These are the factors in your equation.

2(x + 1)(4x + 1)

Method 4 of 6: Difference of Square Roots

Some coefficients in polynomials can be 'squares', or the product of two numbers. Identifying these square numbers allows you to factor multiple polynomials more quickly. Try this equation:

27x² - 12 = 0

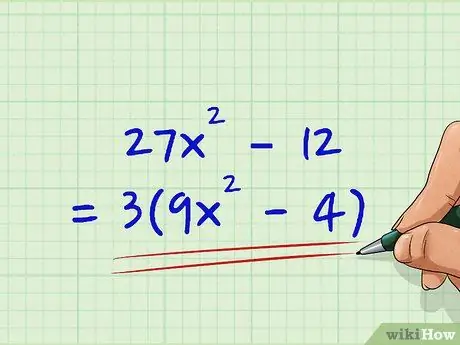
Step 1. Take out the greatest common factor if possible

In this case, we can see that 27 and 12 are divisible by 3, so we get:

27x² - 12 = 3(9x² - 4)

Step 2. Identify if the coefficients of your equation are square numbers

To use this method, you must be able to take the square root of both terms. (Note that we will ignore the negative sign – because these numbers are squares they can be the product of two positive or negative numbers)

9x² = 3x * 3x and 4 = 2 * 2

Step 3. Using the square root you got, write down the factors

We'll take the values of a and c from our step above - a = 9 and c = 4, then find the square root - a = 3 and c = 2. The result is the coefficient of the factor equation:

27x² - 12 = 3(9x² - 4) = 3(3x + 2)(3x - 2)

Method 5 of 6: Quadratic Formula

If all else fails and the equation cannot be factored whole, use the quadratic formula. Try this example:

x² + 4x + 1 = 0

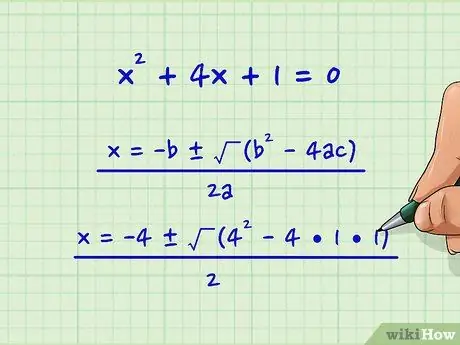
Step 1. Enter the required values in the quadratic formula:

x = -b ± (b² - 4ac)

2a

We get the equation:

x = -4 ± (4² - 4•1•1) / 2

Step 2. Find the value of x

You will get two values. As shown above, we get two answers:

x = -2 + (3) or x = -2 - (3)

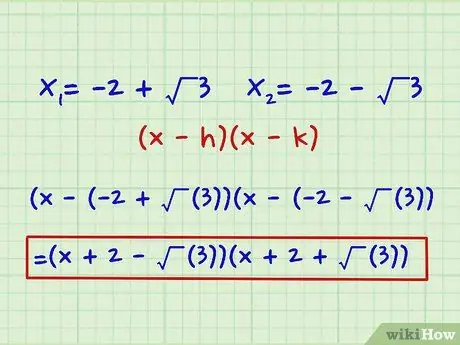
Step 3. Use your x-value to find the factors

Plug the x values you've got into the two polynomial equations as constants. The result is your factors. If we call our answers h and k, we write down the two factors as follows:

(x - h)(x - k)

In this example, our final answer is:

(x - (-2 + (3))(x - (-2 - (3)) = (x + 2 - (3))(x + 2 + (3))

Method 6 of 6: Using the Calculator

If you're allowed to use a calculator, a graphing calculator makes the factoring process a lot easier, especially for standardized tests. These instructions are for the TI graphing calculator. We'll use an example equation:

y = x² x 2

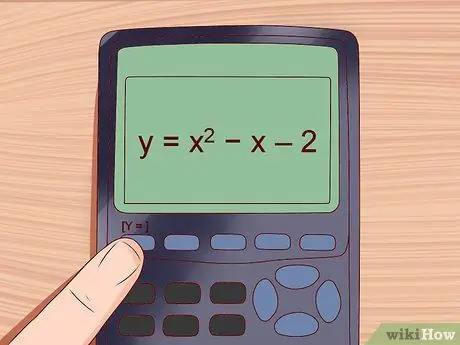
Step 1. Enter your equation into the calculator

You will use the factoring of the equation, which is written [Y =] on the screen.

Step 2. Graph your equation using your calculator

When you have entered your equation, press [GRAPH] – you will see a smooth curve that represents your equation (and the shape is a curve because we are using polynomials).

Step 3. Find the location where the curve intersects with the x-axis

Since polynomial equations are usually written as ax² + bx + c = 0, this intersection is the second value of x that causes the equation to be zero:

(-1, 0), (2, 0)

x = -1, x = 2

If you can't identify where the graph intersects with the x-axis by looking at it, press [2nd] and then [TRACE]. Press [2] or select zero. Move the cursor to the left of the intersection and press [ENTER]. Move the cursor to the right of the intersection and press [ENTER]. Move the cursor as close to the intersection as possible and press [ENTER]. The calculator will find the value of x. Do this for the other intersections as well

Step 4. Plug the x value obtained from the previous step into the two factorial equation

If we named both of our x values h and k, the equations we would use would be:

(x - h)(x - k) = 0

Thus, our two factors are:

(x - (-1))(x - 2) = (x + 1)(x - 2)

Tips

• If you have a TI-84 calculator (graph), there is a program called SOLVER that will solve your quadratic equations. This program will solve polynomials of any degree.
• If a term is not written, the coefficient is 0. It is helpful to rewrite the equation if this is the case, for example: x² + 6 = x² +0x+6.
• If you factored your polynomial using a quadratic formula and got the answer in terms of roots, you might want to convert the value of x to a fraction to check.
• If a term has no written coefficient, the coefficient is 1, for example: x² = 1x².
• After enough practice, you'll eventually be able to factor polynomials in your head. Until you can do it, make sure to always write down the how-to.