- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-01-23 12:04.
While it may seem daunting at times, the square root problem is actually not that difficult to solve. Simple square root problems can usually be solved as easily as basic multiplication and division problems. For more complex questions, it takes a little extra effort. But with the right approach, any difficult problem can be solved. Through this article we will help you solve square root problems in a few easy steps.
Step
Part 1 of 3: Understanding Squares and Square Roots
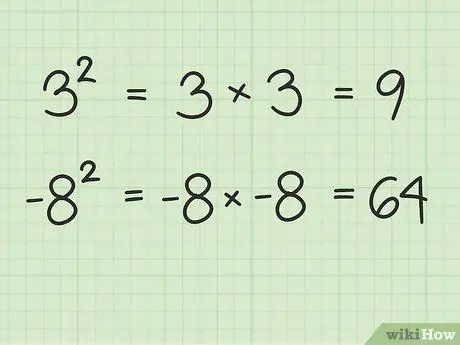
Step 1. The square is the number multiplied by the number itself
To understand the square root, it's good we understand the meaning of the square first. Simply put, a square is a number multiplied by the number itself. For example, 3 squared is 3 times 3 = 9 and 9 squared is 9 times 9 = 81. The square is represented by the small 2 at the top right of the number squared - like this: 32, 92, 1002, etc.
Try squaring some other numbers to test this concept. Remember, squaring a number is multiplying a number by itself. You can even square negative numbers. The result will always be a positive number. For example, -82 = -8 × -8 = 64.
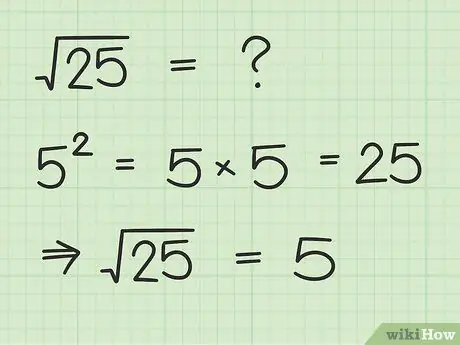
Step 2. The square root is the reciprocal of the square
The symbol for the square root (√, also known as the "radical" symbol) is essentially the opposite of the symbol 2. When you find a radical, ask yourself: what number, if squared, would result in the number inside the radical? For example, if you see (9), find a number that squares the result to nine. Thus, the answer is "three", because 32 = 9.
-
As another example, let's try to find the square root of 25 (√(25)). That is, we are looking for a number that when squared, the result is 25. Because 52 = 5 × 5 = 25, then (25) =
Step 5..
-
The square root can also be considered "undoing" the square. For example, if we want to find (64), the square root of 64, then think of 64 as 82. Since the square root symbol essentially “negates” the square symbol, therefore (64) = (82) =
Step 8..

Step 3. Know the difference between perfect and imperfect squares
Until now, the results of our square root calculations were whole numbers. The questions that you will face later will not be that easy, there will be questions with decimal number answers with a few digits behind the comma. Numbers that are rounded after squaring (that is, not fractional or decimal numbers) are also referred to as “perfect squares”. All of the previous examples (9, 25, and 64) are perfect squares because if they are squared, the result is a whole number (3, 5, and 8).
On the other hand, numbers that are not rounded after being squared, are "imperfect squares". Usually, after squaring the result is a fractional or decimal number. Sometimes even the numbers look very complicated, like (13) = 3, 605551275464…
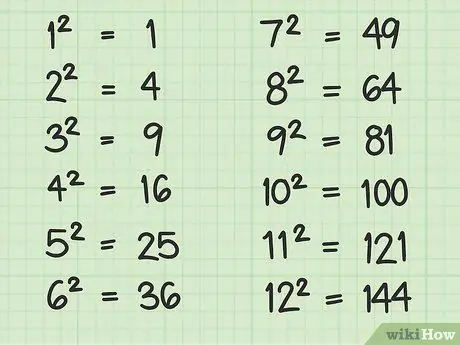
Step 4. Memorize the square of the numbers 1-12
As you already know, squaring a perfect square number is very easy. Memorizing the squares of the numbers 1-12 can be very useful because these numbers will appear a lot in the problem. Thus, you will save time while working on the questions. The first 12 squared numbers are::
-
12 = 1 × 1 =
Step 1.
-
22 = 2 × 2 =
Step 4.
-
32 = 3 × 3 =
Step 9.
-
42 = 4 × 4 =
Step 16.
-
52 = 5 × 5 =
Step 25.
- 62 = 6 × 6 = 36
- 72 = 7 × 7 = 49
- 82 = 8 × 8 = 64
- 92 = 9 × 9 = 81
- 102 = 10 × 10 = 100
- 112 = 11 × 11 = 121
- 122 = 12 × 12 = 144
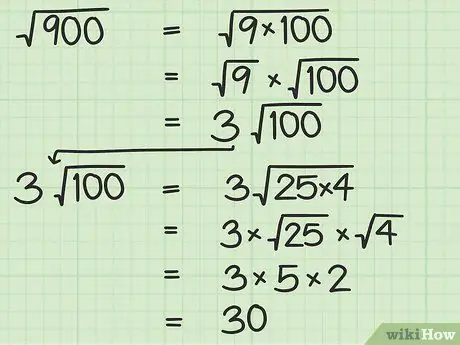
Step 5. Simplify the square root by removing the perfect squares
Finding the square root of an imperfect square number can be difficult, especially if you don't use a calculator. However, the number to be squared can be simplified to make it easier to calculate. To do this, simply separate the number inside the radical into several factors, then remove the square root of the perfect square numbers and write the answer outside the radical. This method is quite easy to do - to give you a better understanding, here's more explanation:
- For example, let's say we want to calculate the square root of 900. So, simply split 900 into several factors. “Factors” are numbers that can be multiplied together to produce another number. For example, the number 6 can be obtained by multiplying and 1 × 6 and 2 × 3, so the factors of 6 are 1, 2, 3, and 6.
- With that principle in mind, let's break down 900 into its factors. To start with, we write 900 as 9 × 100. Since 9 is a perfect square, we can take the square root of 100 separately. (9 × 100) = (9) × (100) = 3 × (100). In other words, (900) = 3√(100).
-
We can simplify it further by separating 100 into its factors, namely 25 and 4. (100) = (25 × 4) = (25) × (4) = 5 × 2 = 10. Therefore, can be calculated (900) = 3(10) =
Step 30..

Step 6. Use an imaginary number for the square root of a negative number
Think, what number if squared the result is -16? The answer, no. All numbers squared are always positive, because they are negative (-), when multiplied by negative the result is positive (+). So, to square a negative number, we need to replace the negative number with an imaginary number (usually in the form of letters or symbols). For example, the variable “i” is generally used for the square root of -1. An imaginary number is always at the square root of a negative number.
It should be noted that although imaginary numbers are never represented by numbers, they can still be treated as numbers in various ways. For example, the square root of a negative number can be squared, to remove the square root. For example, i2 = -1
Part 2 of 3: Use the Long Stacking Division Style Algorithm

Step 1. Solve square root problems like long division problems
Although time-consuming, difficult square root problems can be solved without a calculator. To do this, we will use a method (or algorithm) similar to long stack division.
- Start by writing the square root problem as you would a long division problem. As an example problem, find the root of 6, 45, which is not a whole number. First, we write the radical symbol (√), then below it we write the number we want to take the square of. Then draw a line over the numbers, just like long stacking division. Now, the "√" symbol looks like it has a tail with the number 6.45 at the bottom.
- We'll be writing the numbers above the problem, so make sure you leave some blank space.

Step 2. Group the digits of the number into pairs
First, group the digits of the number under the radical into pairs, starting at the decimal point. Make some sort of marker (period, comma, line, etc.) between pairs for easy tracking.
In the example problem, 6, 45 will be divided into 6-, 45-00. Remember that there are "remaining" digits on the left - this is not a problem.
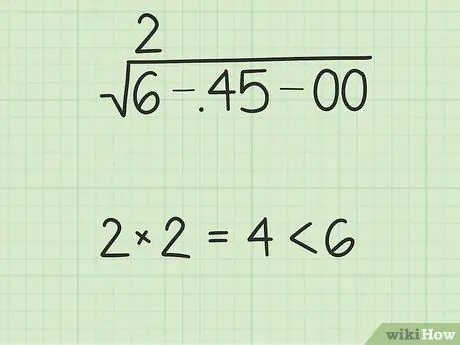
Step 3. Find the largest number whose square value is less than or equal to the first group
Start with the first number in the group on the left. Choose the largest number whose square value is less or equal in the group. For example, if the group is 37, then choose 6 because 62 = 36 < 37 but 72 = 49 > 37. Write this number above the first group. This number is the first digit of your answer.
-
In the example problem, the first group of 6-, 45-00 is 6. The largest number that is less than or equal to 6 when squared is
Step 2. - 22 = 4. Write the number "2" above 6 and the tail is a radical.
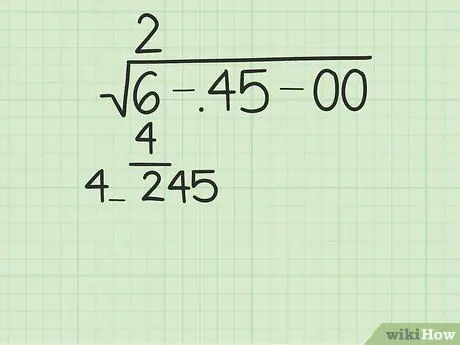
Step 4. Multiply the number you just wrote down, then lower it down and then subtract it
Take the first digit of your answer (written above the radical) and multiply it. Write the answer under the first group and subtract to find the difference. Drop the next group to the right of the difference you just calculated. Finally, write the last digit of multiplying the first digit of your answer on the left and leave a blank space on the right.
In the example problem, the number that is doubled is 2 (the first digit of the previous answer). 2 × 2 = 4. Then, subtract 4 by 6 (from the first group). 6 - 4 the result is 2. Next, bring down the next group (45) and we get 245. Finally, write the number 4 again on the left and leave a little space on the right, like this: 4_
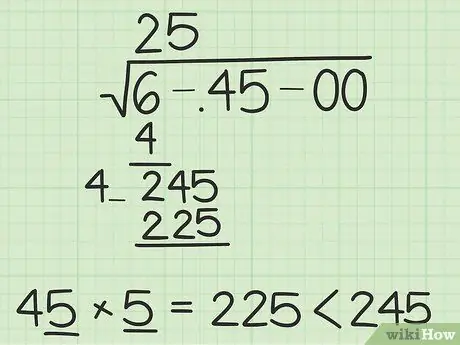
Step 5. Fill in the blank space
Add the digits to the right of the number you wrote on the left. Choose the digit that gives the largest value when multiplied by this new number, but is still less than or equal to the “derived number”. For example, if the “derived number” is 1700 and the number on your left is 40_, the number that should be entered is "4" because 404 × 4 = 1616 < 1700, while 405 × 5 = 2025. The number found in this step is the second digit of your answer, so write it above the radical symbol.
-
In the example problem, we will look for the number next to 4_ × _ whose answer is the largest number but is less than or equal to 245. The answer is
Step 5.. 45 × 5 = 225, while 46 × 6 = 276.

Step 6. Continue to use the “blank space” numbers to find your answer
Continue the long stacking division pattern until the difference between the subtractions of the numbers being derived is zero, or a fairly accurate number has been obtained. When you're done, the numbers you used to fill in the blanks in each step (plus the very first number you used) make up each digit of your answer.
-
In the example problem, subtract 245 by 220 to get 20. Next, we'll lower the next group of digits, 00, and get 2000. Multiply the number above the radical symbol, and we get 25 × 2 = 50. To fill in the blanks at 50_ × _ =/< 2, 000, get the number
Step 3.. Now, we've got "253" above the radical symbol - repeat this process again, and get 9 in the next digit.

Step 7. Remove the decimal sign from the origin
To get the final answer, put the decimal point in the correct position. It's easy - just put the decimal point in line with the decimal point below the radical symbol. For example, the number below the radical is 49, 8, so put a decimal point between the numbers above 8 and 9.
In the example problem, if the number under the radical is 6, 45, then the decimal point will be in line between the digits 2 and 5. This means that the final answer is 2, 539.
Part 3 of 3: Quickly Estimate Imperfect Squares
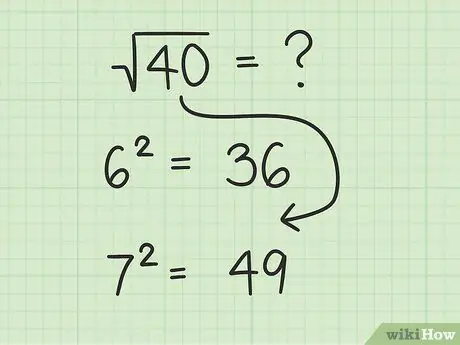
Step 1. Find the imperfect square using approximation
Once you've memorized perfect squares, finding imperfect squares will be much easier. The trick is to find a perfect square before and after the number you're looking for. Then, determine which of the two perfect squares is closest to the number you're looking for.
For example, we want to find the square root of 40. The perfect square number before and after 40 is 62 and 72, which is 36 and 49. Since 40 is greater than 36 and less than 49, the square root of 40 must be between 6 and 7. The number 40 is closer to 36 than 49, so the square root of 40 is closer to 6. Here are a few steps to find an accurate answer.
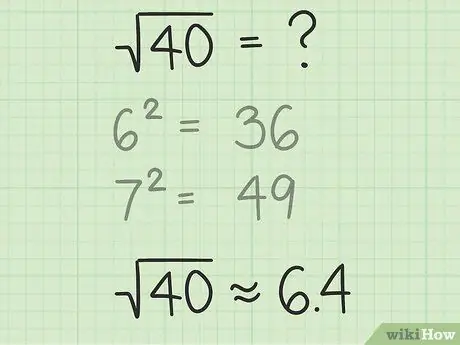
Step 2. Estimate the square root to one digit after the comma
When you have determined two perfect square numbers before and after the number you are looking for, the rest is the process of finding the number behind the comma that is closest to the answer. Start with the estimated one-digit number after the comma. This process will keep repeating until you get an answer with the accuracy you want.
In the example problem, the reasonable approximation of the square root of 40 is 6, 4, because the answer is most likely closer to 6 than 7.

Step 3. Multiply your estimated number by the number itself
In other words, square your approximate number. If you are lucky, the result will be the number in the problem. If not, keep adding or subtracting the numbers after the comma until you find the square that is closest to the number in the problem.
- Multiply 6, 4 by 6, 4 to get 6, 4 × 6, 4 = 40, 96, which is slightly above 40.
- Since the initial experiment was redundant, subtract your approximation by one digit after the comma, which is 6.3 × 6, 3 = 39, 69. This result is slightly below the number in the problem. This means that the square root of 40 is between 6, 3 and 6, 4. Then, since 39.69 is closer to 40, the square root of 40 is also closer to 6, 3.

Step 4. Forward forecasting as needed
Use your answer if you think it's accurate enough. But if not, just continue the approximate pattern above until you find an answer with three or four digits after the comma - basically, until you reach the level of accuracy you want.






