- Author Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
The metric system is a comprehensive system of measurement used throughout the world today. One of the biggest advantages that the metric system offers is that the conversion between units is very simple and logical, because units have a scale rank 10. Because of this, conversion between metric measurements is usually just as easy as multiplying or dividing a given measurement by the power of 10 to find the new value, or simply moving the decimal point. Read on below for more detailed instructions.
Step
Method 1 of 2: Converting Through Multiplication and Division

Step 1. Learn the most frequently used metric prefixes
The metric system has many different units of measurement - you may have heard of the meter (which measures distance) and grams (which measures mass), etc. These base units are sometimes too small or too large to measure in practice. In this case, we need to use units that differ to the power of 10 from the base unit - in other words, measurements that are 10 times larger or smaller, 100 times smaller or larger, and so on. In this case, we add prefixes to the unit name to indicate how much larger or smaller it is compared to the base unit. The most frequently used prefixes, from 1,000 times larger to 1,000 times smaller are:
- Kilo - 1000 times bigger
- Hecto - 100 times bigger
- Deka - 10 times bigger
- Desi - 10 times smaller
- Centigrade - 100 times smaller
- Milli - 1000 times smaller
- An easy trick to remembering these basic metric prefixes is the acronym Brother Henry Likes To Sit With Sweet Girls. The first letter of each word represents the basic metric prefix, from largest to smallest, except for the S in the word Like, which represents the base metric unit or units (meters, liters, etc.)

Step 2. Write the list of prefixes on a line
If you are not familiar with metric units, it can be helpful to list the metric prefixes on a line from largest to smallest. Write Kilos at the far left of the line and Milli at the far right. In the middle, place the Deka and Desi, placing the base units of the dimension you are measuring. In other words, if you measure distance, write meters, if you measure volume, write liters, and so on. This line gives you a simple visual picture of the relationship between your units - whether they are larger or smaller than your own, and how much larger or smaller.

Step 3. Decide if the unit you want is bigger or smaller than the unit you have
Look at your starting line. Look for the prefix that corresponds to the initial unit you have. Next, find the unit you want. Is the unit to the right or to the left of your initial unit? If the unit is on the right, you are converting from the larger unit to the smaller unit. If the unit is on the left, you are converting from the smaller unit to the larger unit.
For example, say we want to find out how long a distance of 10 kilometers is in centimeters. In our prefix line, we'll see that the centi is to the right of the kilo. Since the unit we want is to the right of our initial unit, we know that we are converting from a larger unit to a smaller unit
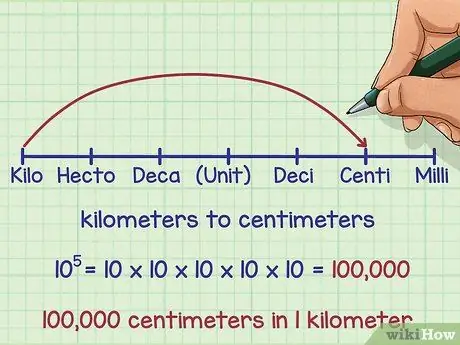
Step 4. Determine the numerical relationship between the units you have and the ones you want
Metric units of measurement have different powers of 10 - 10, 100, 1,000, and so on. Thus, converting from one metric unit to another is always done by multiplying or dividing your original measurement by the appropriate power of ten. Look at the arrows you have drawn from the units you have - your units of measurement - to the units you want. The number of places under your arrow indicates the power of ten connecting your two units.
For example, in our example of a distance of 10 kilometers, we see that our arrow from kilos to centimeters jumps five places. That is, kilometers and centimeters have a different conversion factor of five times to the power of ten, or also written as ten to the power of five, 105, or 10 × 10 × 10 × 10 × 10 = 100,000. In other words, a centimeter is 100,000 times (or 105, etc.) is smaller than kilometers. Thus, you know that there are 100,000 centimeters in 1 kilometer.

Step 5. For a large-to-small conversion, multiply by the appropriate power of ten
Converting from large units to small units means that you have to multiply your original measurement by the difference of the initial units by the unit you want. Remember that this number is the power of ten of the number of places under the arrows you drew in the steps above.
-
Sometimes, especially in homework, it's not enough to just write down the correct answers. You will also be asked to show how you convert your initial units to your final units. In a simple conversion like we're doing now, name your initial unit of measurement as you normally would, then name your conversion factor as a fraction. (desired unit)/(your initial unit of measurement).
The units in the denominator can be crossed out with your original unit of measurement, leaving the answer in the units you want.
-
In our 10 kilometer distance example, we simply multiply 10 (our initial measurement in kilometers) by 105 (or 100,000 - the number of centimeters in a kilometer). See the following:
- 10km × 105 cm/km =
- 10 km × 100,000 cm/km =
- = 1,000,000 cm. There is 1,000,000 centimeters within 10 kilometers of us.
Step 6. For small-to-large conversion, divide by the appropriate power of ten
Converting from small units to large units is basically the opposite - it's not multiplying, you need to divide. Take your initial measurement and divide it by the difference between the initial unit and the unit you want - again, this number must be a power of ten.
- Alternatively, you can multiply it by its inverse power of ten to get the same result. For example, you don't divide the measurement by 103, but you multiply by 10-3. Both operations are correct and will give the same answer.
-
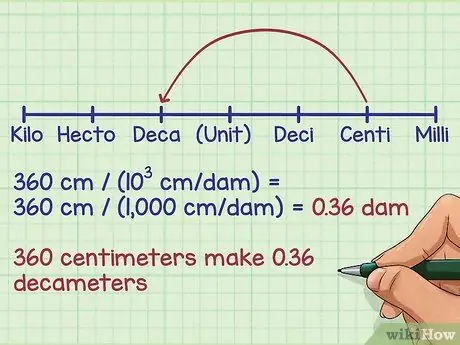
Let's do an example problem. Suppose we want to convert 360 centimeters to decameters. Since the centi and deca are three places apart on the prefix, we know that the decameter is 103 times larger than centimeters. We'll convert it by dividing like this:
- 360cm / (103 cm/dam) =
- 360 cm / (1,000 cm/dam) =
-
= 0.36 check. 360 centimeters to 0, 36 decameter.
Method 2 of 2: Converting Using Decimal Displacement

Step 1. Determine the direction and size of the conversion
This quick method will allow you to easily convert metric units without having to do any multiplication or division. To start with, what you need to know is if you are converting from small units to larger units or vice versa, as well as the conversion size you are using - in other words, if the units you want are 10 different1, 102, etc. from your initial unit.
Both can be determined by counting places and/or drawing a metric prefix arrow. For example, if we want to convert from kilometers to decameters, we know that we are converting from large units to small units because we have to walk to the right along the line from kilos to decameters, and we know that decameters are 102 times smaller than kilometers because kilo and deka are separated by two places.

Step 2. Move the decimal point to your measurement
Since two metric units always differ from each other by multiples of ten, it is possible to convert metrics simply by moving the decimal point of your starting number. When converting from larger units to smaller units, move your decimal point one digit to right for each multiple of ten that differs between your desired unit and your original unit. When converting from small units to larger units, move the decimal place to left.
Remember that the multiple of ten that differs between your desired unit and your original unit is indicated by the number of places separating the two units on the prefix line.
-
For example, say we want to convert 1 kilometer to centimeter. Because we can tell from the prefix that the centimeter is 105 times smaller than kilometers, we move the decimal point at 1 five places to the right. See below:
- 1, 0
- 10, 0
- 100, 0
- 1.000, 0
- 10.000, 0
- 100,000, 0. There 100.000, 0 centimeters in 1 kilometer.
- You can also do the opposite - move the decimal number to the left to convert to a larger unit.

Step 3. Add zeros if needed
When you move the decimal point of a number, make sure to add zeros for each place that exceeds the existing digits. For example, when converting 1 kilometer to centimeters, the decimal point is initially to the right of 1, like so: 1.
Moving the decimal place to the right means you have to add zeros so the number becomes 10.
-
The same principle applies when moving the decimal point to the left - start adding zeros as you move the decimal beyond the existing digits. For example, say we want to convert 1 millimeter to meters. Because meter is 103 times larger than a millimeter, we simply move the decimal three places to the left as follows:
- 1, 0
- 0, 10
- 0, 010. Notice that we add one zero to the left of the number 1.
- 0.0010. We add another zero to get our final answer. There is 0, 001 meters in 1 millimeter.
- Only add zeros if you run out of digits when moving the decimal point. Adding extra zeros in the middle of a number can make your answer wrong.
Tips
-
There are abbreviations for each prefix and units that you can use to make writing easier.
Unit
-
- Meters: m
- Liters: L
- Grams: g
Prefix
-
- Kilo: k
- Hecto: h
- Deka: Da or Dka
- desi: d
- Centi: c
- Milli: m
- There are actually other prefixes used in the SI system, which are very close to the metric system.
- Practice! Gradually, if you've used it often enough, you'll memorize it, and there's no need to draw lines.
Warning
- This method can take up space if you have to do it in an exam. Try not to take up too much space if you decide to use this method.
- Don't use this method if you have other prefixes than those listed above, such as mega or micro.
- Do not use this method if the units are squared, for example if you want to change the meter squared (m2) to centimeter squared (cm2).






