It is easy to multiply fractions by mixed numbers or whole numbers. Start by converting mixed fractions or whole numbers into improper fractions (fractions with a larger numerator than the denominator). Multiply the numerator of the two fractions. After that, multiply the two denominators and simplify the product.
Step
Method 1 of 2: Multiplying Two Mixed Fractions
Step 1. Convert mixed fractions to improper fractions
To convert a mixed number, multiply the denominator by an existing whole number. After that, add a numerator to the product. Place the final result above the line and don't change the denominator. Repeat this step for the other mixed fractions.
For example, if you have a 1 1/2 x 4 4/7 multiplication problem, convert both fractions to improper fractions. The fraction 1 1/2 can be changed to 3/2 and 4 4/7 is turned into 32/7. Now, your multiplication problem becomes 3/2 x 32/7
Step 2. Multiply the numerator of both fractions
Once you have two improper fractions and no more integers in the problem, multiply the two numerators. Write the result and place it above the line.
- The numerator is always at the top of the fraction.
- For example, for the problem 3/2 x 32/7, multiply 3 by 32 to get 96.
Step 3. Multiply the denominators of both fractions
Now multiply the number under the line and write the result under the numerator.
For example, for the problem 3/2 x 32/7, multiply 2 by 7 to get 14
Step 4. Convert answers to mixed fractions if possible
If the numerator of the product is greater than the denominator, find a number that produces a number that approximates the numerator when multiplied by the denominator (this number later acts as an integer). After that, place the difference between the product of the denominator by the whole number and the numerator over the denominator to get the mixed number form.
- For example, if you get 96/14 as the result of multiplying, find the number that results in a sum that is close to 96 when multiplied by 14. That number is 6, and you get 12 as the difference between 14 x 6 and 96. Place 12 above the denominator (14).
- Usually, the teacher will ask you to write the answer in the same form as the question. If you get a mixed number as a problem, you also need to convert the answer to a mixed number.
Step 5. Simplify the results further if possible
It is possible that you will get both whole numbers and fractions. Look at the fractions and check if they can be simplified. For example, if you have a result of 6 12/14, divide 12/14 by 2 to simplify it to 6/7.
In this example problem, your final answer would be 6 6/7
Method 2 of 2: Multiply Fractions by Integers
Step 1. Rewrite the whole number as a fraction
To rewrite an integer as a fraction, simply place it above the number 1 (the denominator). After that, the existing integers will turn into improper fractions.
For example, if you have a problem of 5 x 8/10, place 5 above the number 1. Now the multiplication is 5/1 x 8/10
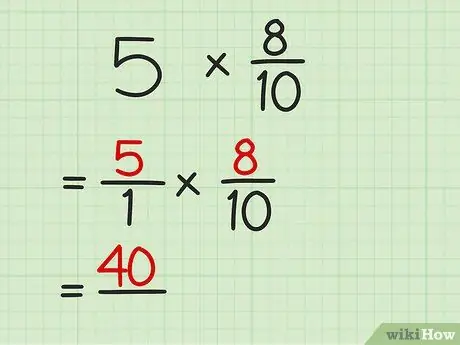
Step 2. Multiply the numerator of both fractions
Remember that the numerator is the number that is above the line. Write down the result and place a line under the product.
For example, in the 5/1 x 8/10 problem, multiply 5 by 8 to get 40
Step 3. Multiply the denominators of both fractions
At this point, you can multiply the numbers below the line to get the denominator of the product. Now you have a multiplication answer in fraction form.
For example, for a 5/1 x 8/10 problem, multiply 1 by 10 to get 10. Place the number under the line so that the product of the two fractions is 40/10
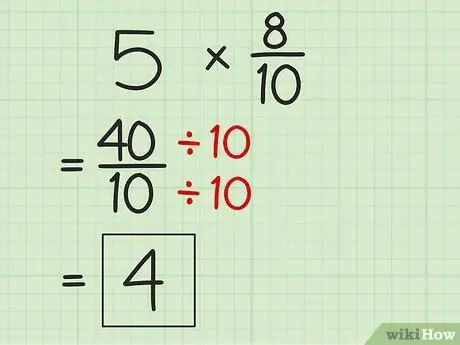
Step 4. Collapse answers if possible
Since the product of the product may be an improper fraction, simplify the result to the smallest form. Divide the numerator by the denominator to get a simpler result.
- To simplify 40/10, divide 40 by 10 to get 4 as the new answer to the multiplication problem.
- Usually, you get mixed numbers because the result of the division will have a remainder.
