3 Ways to Calculate Spearman's Rank Correlation Coefficient

2024 Author: Jason Gerald | [email protected]. Last modified: 2023-12-16 10:50

With Spearman's rank correlation coefficient we can identify whether two variables have a monotonic function relation (that is, when one number increases, the other number will also increase, or vice versa). To calculate Spearman's rank correlation coefficient, you need to rank and compare data sets to find d², and then enter the data into the standard or simplified Spearman rank correlation coefficient formula. You can also calculate these coefficients using Excel formulas or the R command.

Step

Method 1 of 3: Manual way

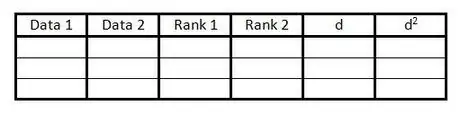
Step 1. Create a table

The table is used to include all the information needed to calculate the Spearman Rank Correlation Coefficient. You need a table like this:

• Create 6 columns with headings, as in the example.
• Prepare as many blank rows as the number of data pairs.

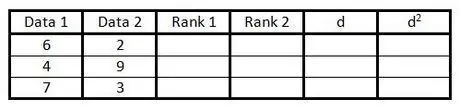
Step 2. Fill in the first two columns with data pairs

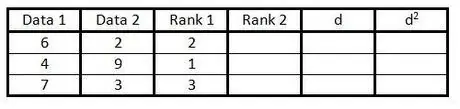
Step 3. Enter the ranking of the first column of data groups in the third column from 1 to n (number of data)

Give a rating of 1 for the lowest value, a rating of 2 for the next lowest value, and so on.

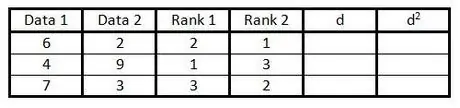
Step 4. In the fourth column, do the same as in step 3, but to rank the data in the second column

• 

  If there are two (or more) data that have the same value, calculate the average rating of the data, then enter it into a table based on this average value.

  In the example on the right, there are two values of 5 in the ratings 2 and 3. Since there are two 5s, find the average of the ratings. The average of 2 and 3 is 2.5, so enter a rating value of 2.5 for both values 5.

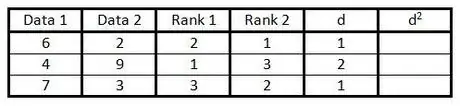
Step 5. In column "d" calculate the difference between the two numbers in the rank column

That is, if one column is ranked 1 and the other column is ranked 3, the difference is 2. (The sign doesn't matter, because the next step is to square the value.)

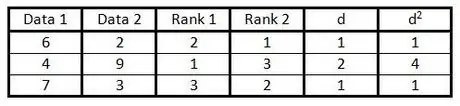
Step 6. Square each number in column "d" and write the result in column "d²".

Step 7. Add up all data in column d²".

The result is d².

Step 8. Choose one of the following formulas:

• If none of the ratings are the same as in the previous step, enter this value in the simplified Spearman Rank Correlation Coefficient formula

  

  and replace "n" with the number of data pairs to get the result.

  

• If there is a similar rank in the previous step, use the standard Spearman Rank Correlation Coefficient formula:

  

Step 9. Interpret the results

The value can vary between -1 and 1.

• If the value is close to -1, the correlation is negative.
• If the value is close to 0, there is no linear correlation.
• If the value is close to 1, the correlation is positive.

Method 2 of 3: Using Excel

Step 1. Create a new column for the data along with its ranking

For example, if your data is in Column A2:A11, use the formula "=RANK(A2, A$2:A$11)", and copy it down until it covers all the columns and rows.

Step 2. Change the same rating as described in steps 3 and 4 of method 1

Step 3. In the new cell, calculate the correlation between the two rank columns with the formula "=CORREL(C2:C11, D2:D11)"

In this example, C and D refer to the column where the ranking is located. The new cell will be filled with the Spearman Rank Correlation.

Method 3 of 3: Using R

Step 1. Install the R program first if you don't have it already

(See

Step 2. Save your data in CSV form, put the data you want to find the correlation in the first two columns

We can do this by using the "Save as" menu.

Step 3. Open the R Editor

If you're working from the terminal, just run R. If you're working from the desktop, click the R icon.

Step 4. Type the following command:

• d <- read.csv("NAME_OF_YOUR_CSV.csv") and press Enter.
• cast(rank(d[, 1]), rank(d[, 2]))

Tips

The data must consist of at least 5 pairs so that the trend can be seen (the number of data is 3 pairs in the example only to simplify calculations.)

Warning

• The Spearman rank correlation coefficient only identifies the strength of the correlation where the data rises or falls consistently. If there is another trend in the data, Spearman's rank correlation no will provide an accurate representation.
• This formula is based on the assumption that there are no equal ratings. When there is the same rank as in the example, we should use this definition: the correlation coefficient of the multiplication moment by rank.