This is an article on how to factor a cube polynomial. We'll explore how to factor using groupings as well as using factors from independent terms.
Step
Method 1 of 2: Factoring by Grouping
Step 1. Group the polynomial into two parts
Grouping a polynomial into two halves will allow you to break each part separately.
Suppose we use a polynomial: x3 + 3x2 - 6x - 18 = 0. Split into (x3 + 3x2) and (- 6x - 18).
Step 2. Find the factors that are the same in each section
- From (x3 + 3x2), we can see the same factor is x2.
- From (- 6x - 18), we can see the equal factor is -6.
Step 3. Take the equal factors out of both terms
- Take out factor x2 from the first part, we get x2(x + 3).
- Taking the factor -6 out of the second part, we get -6(x + 3).
Step 4. If each of the two terms has the same factor, you can combine the factors together
You will get (x + 3)(x2 - 6).
Step 5. Find the answer by looking at the roots of the equation
If you have x2 at the roots of the equation, remember that both positive and negative numbers will satisfy the equation.
The answers are -3, 6 and -√6
Method 2 of 2: Factoring Using Free Terms
Step 1. Rearrange the equation into the form aX3+bX2+cX+d.
Suppose we use a polynomial: x3 - 4x2 - 7x + 10 = 0.
Step 2. Find all the factors of "d"
The constant "d" is a number that doesn't have any variables, such as "x", next to it.
Factors are numbers that can be multiplied together to get another number. In this case, the factors of 10, which is "d", are: 1, 2, 5, and 10
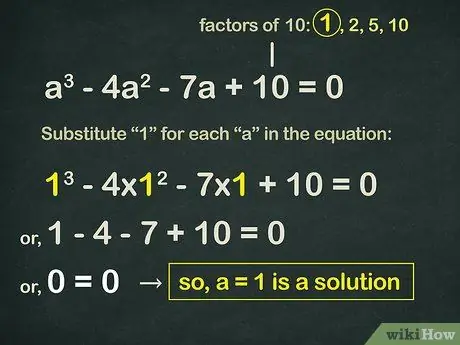
Step 3. Find one factor that makes the polynomial equal to zero
We must determine which factors make the polynomial equal to zero when we substitute factors into each "x" in the equation.
-
Start with the first factor, which is 1. Substitute "1" for each "x" in the equation:
(1)3 - 4(1)2 - 7(1) + 10 = 0.
- You will get: 1 - 4 - 7 + 10 = 0.
- Since 0 = 0 is a true statement, you know that x = 1 is the answer.
Step 4. Do some settings
If x = 1, you can rearrange the statement to make it look slightly different without changing its meaning.
"x = 1" is the same as "x - 1 = 0". You just subtract by "1" from each side of the equation
Step 5. Take the root factor of the equation from the rest of the equation
"(x - 1)" is the root of the equation. Check if you can factor out the rest of the equation. Take out the polynomials one by one.
- Can you factor out (x - 1) from x3? No. But you can borrow -x2 of the second variable, then you can factor it: x2(x - 1) = x3 - x2.
- Can you factor (x - 1) out of the remainder of the second variable? No. You have to borrow a bit from the third variable. You have to borrow 3x from -7x. This will give the result -3x(x - 1) = -3x2 + 3x.
- Since you took 3x from -7x, the third variable becomes -10x and the constant is 10. Can you factor it? Yes! -10(x - 1) = -10x + 10.
- What you do is set the variable so that you can factor out (x - 1) from the whole equation. You rearrange the equation to something like this: x3 - x2 - 3x2 + 3x - 10x + 10 = 0, but the equation remains the same as x3 - 4x2 - 7x + 10 = 0.
Step 6. Continue substituting with factors of the independent term
Look at the number you factored using (x - 1) in step 5:
- x2(x - 1) - 3x(x - 1) - 10(x - 1) = 0. You can rearrange it to make it easier to factor once again: (x - 1)(x2 - 3x - 10) = 0.
- Here, you only need to factor (x2 - 3x - 10). The result of factoring is (x + 2)(x - 5).
Step 7. Your answer is the factored roots of the equation
You can check whether your answer is correct by plugging each answer, separately, into the original equation.
- (x - 1)(x + 2)(x - 5) = 0. This will give the answers 1, -2 and 5.
- Plug -2 into the equation: (-2)3 - 4(-2)2 - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0.
- Plug 5 into the equation: (5)3 - 4(5)2 - 7(5) + 10 = 125 - 100 - 35 + 10 = 0.
Tips
- There is no cube polynomial that cannot be factored using real numbers because every cube always has a real root. A cube polynomial like x3 + x + 1 which has an irrational real root cannot be factored into a polynomial with integer or rational coefficients. Although it can be factored by the cube formula, it cannot be reduced as an integer polynomial.
- A cube polynomial is the product of three polynomials to the power of one or the product of a polynomial to the power of one and a polynomial to the power of two that cannot be factored. For situations like the latter, you use long division after finding the first power polynomial to get the second power polynomial.
